2021 RoboCom 世界机器人开发者大赛-高职组(决赛)题解
目录
题目:7-1 小偷踩点(20分)
输入格式:
输出格式:
输入样例
输出样例:
解题思路:
具体代码:
题目:7-2 盲盒包装流水线 (25 分)
输入格式:
输出格式:
输入样例:
输出样例:
解题思路:
具体代码:
题目:7-3 到底爱不爱我(25分)
输入格式:
输出格式:
输入样例:
输出样例:
样例说明:
解题思路:
具体代码:
题目:7-4 皆大欢喜(30分)
输入格式:
输出格式:
输入样例:
输出样例:
解题思路:
具体代码:
题目:7-1 小偷踩点(20分)
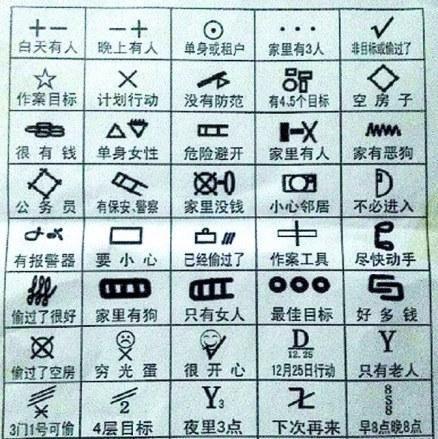
俗话说不怕贼偷,就怕贼惦记。
小偷在作案前有时会在居民家的门、墙上做一些标记,每一种记号代表一个含义,一般人看不懂,但同行一看便知道这个家庭的情况。不过派出所干警也不是吃素的,很快破译了这些记号的含义(如上图),并且在辖区内广为张贴,告知居民。
随后小偷们又改变了方法,将这些记号从 1 到 N 编号,然后将这些编号按照某种规则重新打乱再做标记,标记变成了一串数字。不过这种新的编号方法又被破译了!干警们发现这些数字的规律可以用一个二维矩阵来表示:矩阵有 10 列,顺序对应数字 0 到 9;矩阵一般不超过 10 行,每行对应一个 0 到 9 之间的数字,这些数字保证不重复。小偷的新标记由若干个两位数组成,每个数字的十位对应行、个位对应列,而对应位置上的数字就是原始标记的编号。
如上图 40 种标记从上到下、从左到右顺序编号后,按下图所示的规律打乱,则如果我们看到标记“71”,就是行标记为 7,列标记为 1 的单元格对应的数字 11,对应原始标记中第 11 个,即“很有钱”。那么标记“71 78 57”就表示原始标记的第 11、8、7 号,意思是“很有钱”、“没有防范”、“计划行动”。
输入格式:
输入第一行给出 2 个正整数:N(≤100)为小偷的原始标记个数,M(≤10)为新标记对照矩阵的行数。
随后 N 行,第 i 行给出第 i 个标记的解释,由不超过 100 个英文字母和空格组成。
接下来一行给出 M 个数字,为 0 到 9 之间的数字,保证不重复,其中第 i 个数对应矩阵第 i 行。
接下来 M 行,每行给出 10 个数字,或者是 1 到 N 之间的一个编号,或者是 −1 表示没有对应的编号。
最后一行给出小偷留在墙上的数字标记,格式为:
k t[1] ... t[k]
输出格式:
对小偷留下的每个数字,在一行中输出其对应的意义,顺序与输入顺序相同。如果没有对应的意义,则在对应行中输出 ?。
输入样例
10 2
jia li you ren
kong fang zi
jia you e gou
dan shen
hen you qian
xiao xin lin ju
you bao jing qi
jin kuai dong shou
xia ci zai lai
bu bi jin ru
6 2
-1 6 5 1 -1 10 3 4 -1 9
2 4 7 -1 3 -1 5 -1 8 2
5 20 64 61 22 13
输出样例:
kong fang zi
?
xiao xin lin ju
you bao jing qi
?
解题思路:
首先我们来理解一下该题的题目大意:给你n个标记解释并依次编号(1~n),再给你矩阵的m个行标以及该m行各列的内容(即标记解释 的编号) 然后给你k个询问,每个询问由两位数组成(十位表示行标,个位表示列表),从矩阵中得到对应的编号, 如果编号为'-1',则表示没有对应的编号,输出'?';否者输出该编号对应的标记解释;
所以,我们可以用一个字符串组储存该n个标记解释,一个二维数组储存矩阵,一个数组存储询问; 具体过程详见如下代码 (要特别留意输入部分的相关代码)
具体代码:
#include
#include
#include
#include
using namespace std;
string s[105];
int mp[10][10];//二维数组表示矩阵
int n,m,k;
int query[105];//询问
int main()
{
cin>>n>>m;
getchar();//将缓冲区的换行符删去,也可以用cin.ignore()替换
for(int i=1;i<=n;i++)
getline(cin,s[i]); //输入n个标记的解释
//注:getline(cin,s[])可以读入带空格的一行字符串
int r[15]; //记录m个行标
for(int i=1;i<=m;i++)
cin>>r[i];
memset(mp,-1,sizeof mp);//将mp初始化为-1,表示没有对应的编号
for(int i=1;i<=m;i++) //输入矩阵的内容
for(int j=0;j<=9;j++)
cin>>mp[r[i]][j];
cin>>k;
for(int i=1;i<=k;i++) //输入k个询问
cin>>query[i];
for(int i=1;i<=k;i++){
int R,C; //R:行标;C:列标
R=query[i]/10; //十位表示矩阵对应的行标
C=query[i]%10; //个位表示矩阵对应的列标
int t = mp[R][C]; //在矩阵中找到对应的编号
if(t==-1) cout<<"?"< 题目:7-2 盲盒包装流水线 (25 分)
众所周知,PAT 有 9 枚徽章,分别对应青铜、白银、黄金、白金、钻石、大师、王者、大圣、天神这 9 个段位,只有成绩非常优秀的考生才有资格获得刻有自己名字的徽章。现在,PAT 制作了徽章的小型纪念版,要制成盲盒给大家玩了!
下图是一条盲盒包装流水线的示意图。首先徽章通过进货口被压入货栈里,空盒在履带上从左向右传送。每次从货栈里弹出一枚徽章,进入打包机,装入一只空盒,打包后继续向右边传送。当货栈为空时,打包机会暂停,等待下一批徽章压入货栈。
每只盒子都有一个编号,小拼姐姐手里有进入流水线的空盒编号顺序表,也有每一批送往货栈的徽章顺序表,这样她其实可以知道每只盒子里装了哪种徽章。有些小朋友收到了盲盒,就想在拆封前问无所不知的小拼姐姐,盒子里的徽章是哪一种。但是因为盲盒总量有 105 这么多,小拼姐姐可记不住每只盒子里装的是什么,于是你就被请来写个程序帮小拼姐姐回复这种信息。
输入格式:
输入第一行给出 2 个正整数,分别为盲盒总量 N(≤105)和货栈容量 S(≤100)。接下来一行给出 N 只盒子的编号,编号由 5 位数字组成,给出的顺序是空盒进入传送带的顺序。随后 N/S(保证是整数)行,每行给出一批 S 枚徽章的类型,为 1-9 的数字,给出的顺序是从进货口入栈的顺序。
再下面给出一个正整数 K(≤104),为查询次数。随后 K 行,每行给出一个 5 位编号。
输出格式:
对每个查询编号,在一行中输出该盒子中装的徽章类型。如果编号是错误的,则在一行中输出 Wrong Number。
输入样例:
10 5
00132 10093 92001 23333 66666 88888 09009 34658 82750 69251
1 2 3 4 5
9 8 7 6 1
5
66666
88888
69251
55555
10093
输出样例:
1
1
9
Wrong Number
4
解题思路:
对于盲盒,我们用一个一维数组来存储; 对于徽章,我们也可以用一个一维数组来存储; (或者用二维数组也可,只需通过盲盒的下标来求其在矩阵的行标和列标) 在这里,我用一维数组来存储; 此时,盲盒和徽章分别在两个一维数组上,并且盲盒与其对应的徽章在各自的数组中的下标是相同的, 所以我们只需保存每个盲盒的下标,当询问时,我们只要用该下标到徽章所在的数组中找,就可得到其对应的徽章;
具体代码:
#include
#include
#include
#include
using namespace std;
const int N = 1e5+10;
const int M = 1e6;
int n,s,k; //n(<=1e5)表示盲盒总量,s(<=100)表示货栈容量 ,k表示询问的次数
int a[N]; //记录盲盒的编号
int huo[102]; //存储货栈的s个徽章对应的号码
int res[N]; //用于存储n个徽章对应的号码
bool st[N]; //st[i]标记编号i是否存在
int sub[M]; //sub[i]存储编号 i 在数组a中的下标
int main()
{
cin>>n>>s;
for(int i=1;i<=n;i++){
cin>>a[i]; //输入盲盒编号
st[a[i]]=true; //标记盲盒编号a[i]存在
sub[a[i]]=i; //盲盒编号a[i]在数组a中的下标为 i
}
int t = n/s; //计算会有多少个货栈
for(int i=1;i<=t;i++){
for(int j=1;j<=s;j++)
cin>>huo[j]; //输入该货栈的各值
for(int j=1;j<=s;j++) //将该货栈的各值放到数组res的对应位置上
res[(i-1)*s+j]=huo[s+1-j];
}
cin>>k;
int query;
//k个询问
for(int i = 1; i <= k; i ++){
cin>>query;
if(!st[query]) cout<<"Wrong Number"< 题目:7-3 到底爱不爱我(25分)
古代少女有了心上人时,会悄悄折一条树枝,揪那枝上的叶子,揪一片叶子念一句“爱我”,再揪一片念一句“不爱我”…… 这样揪落最后一片叶子的时候,看看是停在“爱”还是“不爱”。
但聪明的慧娘一眼洞穿,只要数一下叶子有多少片,根据这个数字的奇偶性判断是以“爱”开始还是以“不爱”开始,就总是可以最后落在“爱”上。这个游戏顿时就变得无趣了 —— 真的是文科生制造浪漫,理科生杀死浪漫。
于是有着工科生大脑的慧娘打算另外制作一个更有趣的浪漫游戏。她用不同植物的枝条做成了三种“情枝”:
- “专情枝”:是一根有两个分岔的树枝,只有当两个分岔上连接的枝条传过来的情话都是“爱”的时候,这根枝条的根部才传出“爱”;否则树枝根部传出的是“不爱”。
- “博爱枝”:也是一根有两个分岔的树枝,只有当两个分岔上连接的枝条传过来的情话都是“不爱”的时候,这根枝条的根部才传出“不爱”;否则树枝根部传出的都是“爱”。
- “情变枝”:是没有分岔的一根直枝,如果一端接到“爱”,另一端必须传出“不爱”;反之如果一端接到“不爱”,另一端则会传出“爱”。
慧娘将这些树枝摆放在院子里,布了一个“情阵”,先选一根特殊的枝条作为初试一枝,从这枝条的根部开始,扩散开去,令它们根枝相连。然后她在末梢的枝杈旁随意写下“爱”或“不爱”。现在请你写个程序帮她算出来,在初始一枝的根部,她能得到“爱”还是“不爱”?
输入格式:
输入在第一行中给出正整数 N(≤30),是慧娘制作的情枝数量。这里假设她将所有的情枝从 1 到 N 做好了编号。随后 N 行,第 i 行给出第 i 枝的描述,格式为
类型 左分枝连接的编号 右分枝连接的编号
其中 类型 为 1 代表专情、2 代表博爱、3 代表情变。当然如果是情变枝,则后面跟的是其唯一末端连接的情枝编号,并没有两个分枝的信息。如果一个分枝是末梢,并没有连接其它枝条,则对应编号为 0。
接下来一行中给出正整数 K(≤30),是慧娘询问的次数。以下 K 行,每行给出一个由 0 和 1 组成的字符串,其中 0 表示“不爱”,1 表示“爱”—— 这是慧娘从左到右在每个枝杈末梢处写下的。(注意:“从左到右”的意思是,我们从初试一枝出发去遍历所有枝条的末梢时,总是遵循先遍历左边情阵、再遍历右边情阵的顺序)
输出格式:
对慧娘的每个询问,如果她在初始一枝的根部能得到“爱”,就输出 Ai;否则输出 BuAi。
输入样例:
6
2 6 4
1 0 0
3 1
2 0 0
3 0
1 5 2
5
11111
00000
11100
10011
01100
输出样例:
BuAi
Ai
Ai
BuAi
BuAi
样例说明:
样例对应的情阵以及慧娘第 3 问的情势如图所示,其中完整的心对应 1,裂开的心对应 0。
解题思路:
三种类型,也就是三种运算,取反,或,非;
刚好这里给的也是 1 表示 爱,0 表示 不爱;
建立一棵树,从根节点开始跑dfs,一直跑到叶节点,然后再从叶节点更新上来;
具体代码:
#include
#include
#include
#include
using namespace std;
const int N = 100; //这里尽量开大一点
//classer[]保持每个枝条的种类,pa[]保存父枝条;
int e[N], classer[N], ne[N], pa[N], h[N], idx ;
char str[N];
queue q;
//用邻接表来存储树
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], pa[b] = a, h[a] = idx++;
}
//将询问输入的字符串转化为整数并用队列来存储
void reform(char str[])
{
int len = strlen(str);
for (int i = 0; i < len; i++)
{
int num = str[i] - '0';
q.push(num);
}
}
//dfs(i)表示返回第 i 个枝条的根部状态
int dfs(int node)
{
//如果当前枝条后面已没有枝条
if (h[node] == -1)
{
//left,right 保存枝条末梢状态
//ans 保存根部状态
int left, right, ans;
//若为 "专情枝" ,做 '与'运算
if (classer[node] == 1)
{
left = q.front(), q.pop(); //从队首取出状态
right = q.front(), q.pop();
ans = left & right;
}
//若为 "博爱枝" ,做 '或'运算
else if (classer[node] == 2)
{
left = q.front(), q.pop();
right = q.front(), q.pop();
ans = left | right;
}
//若为 "情变枝" ,做 '非' 运算
else if (classer[node] == 3)
{
left = q.front(), q.pop();
ans = !left;
}
return ans;
}
//当前枝条后面还有枝条时
int son_node[2], sub = 0; //son_node[]记录当前枝条的左右分枝
//son_node[0]即左分枝,son_node[1]即右分枝;
int num1, num2, ans; //num1保存左枝的状态,num2保存右枝的状态,ans保存结果;
for (int i = h[node]; i != -1; i = ne[i]) //通过邻接表找到其左右分枝
son_node[sub++] = e[i];
//若为 "专情枝" ,做 '与'运算
if (classer[node] == 1){
if (son_node[0]!=0) num1=dfs(son_node[0]); //若不为'0',则存在左枝条,用dfs求出
else{ //若为'0',则为末梢,从队列中读取
num1=q.front();
q.pop();
}
if (son_node[1]!=0) num2=dfs(son_node[1]); //若不为'0',则存在右枝条,用dfs求出
else { //若为'0',则为末梢,从队列中读取
num2=q.front();
q.pop();
}
ans=num1 & num2;
}
//若为 "博爱枝" ,做 '或'运算
else if (classer[node] == 2){
if (son_node[0]!=0) num1=dfs(son_node[0]); //同上
else{
num1=q.front();
q.pop();
}
if (son_node[1]!=0) num2=dfs(son_node[1]);
else {
num2=q.front();
q.pop();
}
ans=num1 | num2;
}
//若为 "情变枝" ,做 '非' 运算
else if (classer[node] == 3)
ans = !dfs(son_node[0]);
return ans;
}
int main()
{
memset(h, -1, sizeof h); //对邻接表进行初始化
memset(pa, -1, sizeof pa); //对父节点进行初始化
int n;
scanf("%d", &n);
int race, left, right;//race记录类型;left记录左子节点,right记录右子节点;
//用邻接表来构建树
for (int i = 1; i <= n; i++)
{
scanf("%d", &race);
classer[i] = race; //classer保存每个枝条的种类;
if (classer[i] == 1 || classer[i] == 2)
{
scanf("%d%d", &left, &right);
//if里面取‘或’运算是因为当left和right都为零时,即左右枝条都不存在时,我们不需要将其插入到邻接表中
//此时,我们就只需保证 h[i]为 '-1';
if (left != 0 || right != 0)
add(i, right), add(i, left);
//注意:该处不可以反过来写成"add(i, left),add(i, right);
//因为如果反过来写,则不能保证题目中的 "从左到右 ";
//具体原因可以通过邻接表的存储方式的规则可知。
}
else if (classer[i] == 3)
{
scanf("%d", &left);
if (left != 0)
add(i, left);
}
}
//找根节点
int root;
for (int i = 1; i <= n; i++)
{
if (pa[i] == -1)
{
root = i;
break;
}
}
//进行 k 个询问
int k;
scanf("%d", &k);
while (k--)
{
scanf("%s", str);
reform(str); //将字符串转化为整型
int ans = dfs(root);//从根节点开始dfs
if (ans)
printf("Ai\n");
else
printf("BuAi\n");
}
return 0;
}
题目:7-4 皆大欢喜(30分)
喵星人素以有个性著称,铲屎官很难用一种玩具让家里所有的喵主子都高兴起来。于是铲屎官调研了一下各种玩具,记录下每种玩具能让哪些喵高兴、同时让哪些喵生气、另外还有哪些喵无感。现在铲屎官来向你求助,请你告诉他如何用最少的玩具,让所有的喵都高兴起来。
注意:如果一只喵处于高兴的状态,那么它会一直高兴着,直到见到让它生气的玩具;同样地,如果喵不高兴,它会一直不高兴,直到见到让它高兴的玩具。如果一样玩具令喵无感,则不会改变它原来的状态。
输入格式:
输入第一行给出两个正整数,分别是 N (≤10),为喵的个数;以及 M(≤10),为玩具的个数(假设玩具从 1 到 M 编号)。随后 M 行,每行对应一种玩具,顺序给出 N 只喵的状态:1 表示高兴,-1 表示生气,0 表示无感。
输出格式:
假设初始状态下没有玩具,所有喵都不高兴。在一行中给出逗喵玩具的编号顺序,使得按这个顺序把玩具给喵,能令所有的喵都高兴起来。要求输出最少玩具的解。当这种解不唯一时,输出最小编号序列。题目保证存在解。一行中的数字以 1 个空格分隔,行首尾不得有多余空格。
序列 { a1,a2,...,an } 小于序列 { b1,b2,...,bn } 的定义是:存在 1≤k 3 4 3 1 4 直接 dfs 爆搜 + 剪枝 遍历所有玩具选择的顺序,然后判断猫的情感状态。输入样例:
-1 1 0
1 1 -1
0 -1 1
1 0 0输出样例:
解题思路:
具体代码:
//回溯:第 i个位置选择某个玩具的所有情况都遍历后,第 i个位置选择下一个玩具。
#include