Pytorch 正则化方法(权重衰减和Dropout)
正则化方法(权重衰退和Dropout)
正则化方法和以前学过的正则表达式没有任何关系!
花书 p141 说到:
能显式地减少测试误差(可能会以增大训练误差为代价)的方法都被称为正则化。
0. 环境介绍
环境使用 Kaggle 里免费建立的 Notebook
教程使用李沐老师的 动手学深度学习 网站和 视频讲解
小技巧:当遇到函数看不懂的时候可以按 Shift+Tab 查看函数详解。
1. 权重衰减
权重衰减是正则化方法之一,权重衰减通过 L2 正则项使得模型参数不会过大,减少噪声的影响,从而控制模型复杂度。
我学这个权重衰减一开始就是学得迷迷糊糊的。
大家可以看一下这个视频看看能不能理解:王木头学科学。
李老师Q&A:
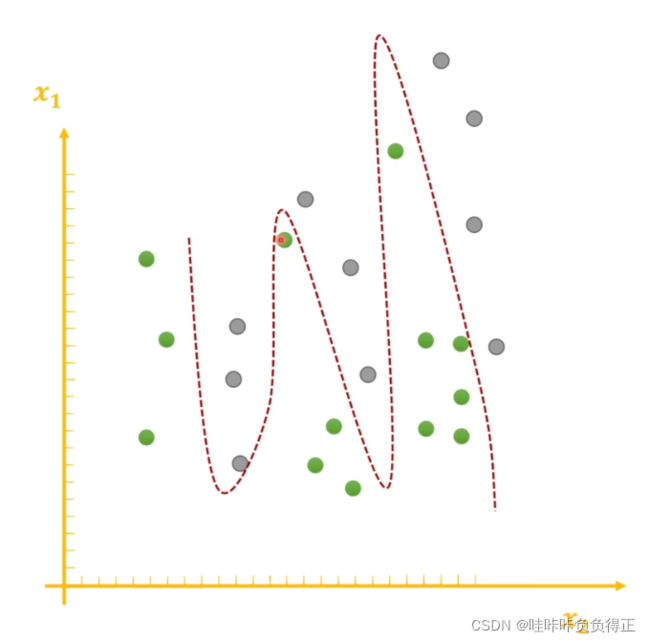
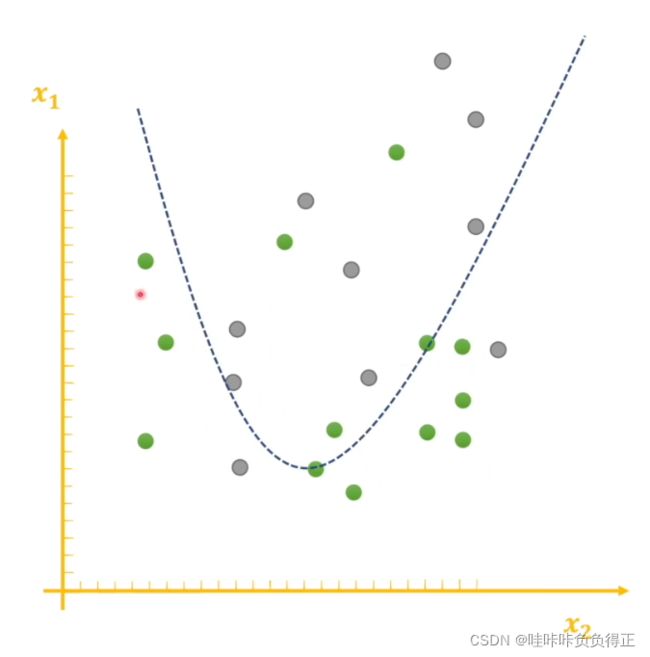
为什么控制模型参数值变小就可以减少模型复杂度?
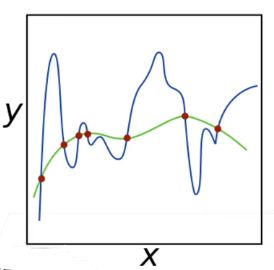
如果不限制 w 的取值,有大有小就会导致得到的结果类似于上图中的蓝线(比较复杂的曲线)。如果控制 w 的取值得到类似于上图绿线的结果(比较平滑的曲线)。
1.1 使用均方范数作为硬性限制
通过限制参数值的选择范围来控制模型容量:
min ℓ ( w , b ) subject to ∥ w ∥ 2 ≤ θ \min \ell(\mathbf{w}, b) \quad \text {subject to }\|\mathbf{w}\|_{2} \leq \theta minℓ(w,b)subject to ∥w∥2≤θ
通常不限制偏移 b (限不限制都差不多),b 不会改变函数的形状,只会改变模型的平移情况。
小的 θ \theta θ 意味着更强的正则项。
1.2 使用均方范数作为柔性限制
对于每个 θ \theta θ,都可以找到 λ \lambda λ 使得之前的目标函数等价于:
min ℓ ( w , b ) + λ 2 ∥ w ∥ 2 \min\quad \ell(\mathbf{w}, b)+\frac{\lambda}{2}\|\mathbf{w}\|_{2} minℓ(w,b)+2λ∥w∥2
超参数 λ \lambda λ 控制了正则项的重要程度
- λ = 0 \lambda=0 λ=0:无作用
- λ → ∞ , w ∗ → 0 \lambda \rightarrow \infty, \mathbf{w}^{*} \rightarrow 0 λ→∞,w∗→0
1.3 演示对最优解的影响
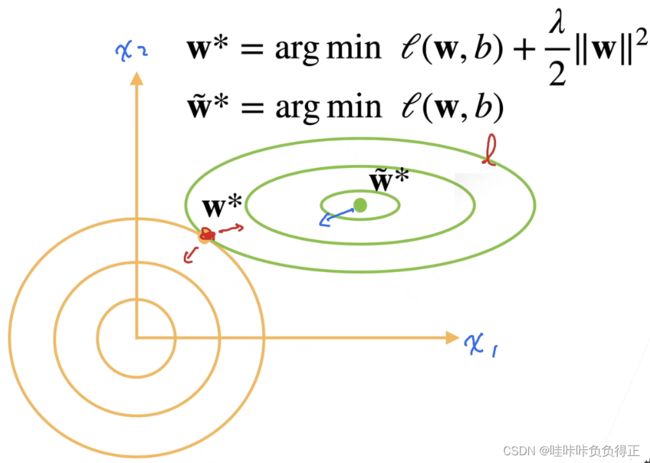
λ 2 ∥ w ∥ 2 \frac{\lambda}{2}\|w\|^2 2λ∥w∥2 也被称为惩罚项,较小的 λ \lambda λ 值对应较少 w w w 约束的, 而较大的 λ \lambda λ 值对 w w w 的约束更大。
1.4 参数更新法则
计算梯度:
∂ ∂ w ( ℓ ( w , b ) + λ 2 ∥ w ∥ 2 ) = ∂ ℓ ( w , b ) ∂ w + λ w \frac{\partial}{\partial \mathbf{w}}\left(\ell(\mathbf{w}, b)+\frac{\lambda}{2}\|\mathbf{w}\|_{2}\right)=\frac{\partial \ell(\mathbf{w}, b)}{\partial \mathbf{w}}+\lambda \mathbf{w} ∂w∂(ℓ(w,b)+2λ∥w∥2)=∂w∂ℓ(w,b)+λw
时间 t 更新参数:
w t + 1 = ( 1 − η λ ) w t − η ∂ ℓ ( w t , b t ) ∂ w t \mathbf{w}_{t+1}=(1-\eta \lambda) \mathbf{w}_{t}-\eta \frac{\partial \ell\left(\mathbf{w}_{t}, b_{t}\right)}{\partial \mathbf{w}_{t}} wt+1=(1−ηλ)wt−η∂wt∂ℓ(wt,bt)
通常 η λ < 1 \eta \lambda<1 ηλ<1,在深度学习中通常叫做权重衰退。
2. 权重衰减代码
2.0 导入模块
#!pip install -U d2l
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
2.1 生成数据
按照公式生成数据:
y = 0.05 + ∑ i = 1 d 0.01 x i + ϵ where ϵ ∼ N ( 0 , 0.0 1 2 ) . y = 0.05 + \sum_{i = 1}^d 0.01 x_i + \epsilon \text{ where } \epsilon \sim \mathcal{N}(0, 0.01^2). y=0.05+i=1∑d0.01xi+ϵ where ϵ∼N(0,0.012).
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)
我们选择标签是关于输入的线性函数。 标签同时被均值为 0 0 0,标准差为 0.01 0.01 0.01 高斯噪声破坏。 为了使过拟合的效果更加明显,我们可以将问题的维数增加到 d = 200 d=200 d=200, 并使用一个只包含 20 20 20 个样本的小训练集,以及 100 100 100 个样本的测试集。
2.2 初始化参数模型
def init_params():
w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
return [w, b]
2.3 定义 L2 范数惩罚
def l2_penalty(w):
return torch.sum(w.pow(2)) / 2
如果想变成 L1 范数惩罚只需要将 torch.sum(w.pow(2)) / 2 变成 torch.sum(torch.abs(w))。
2.4 定义训练代码实现
def train(lambd):
w, b = init_params()
net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss
num_epochs, lr = 100, 0.003
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
for X, y in train_iter:
# 增加了L2范数惩罚项,
# 广播机制使l2_penalty(w)成为一个长度为batch_size的向量
l = loss(net(X), y) + lambd * l2_penalty(w)
l.sum().backward()
d2l.sgd([w, b], lr, batch_size)
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
print('w的L2范数是:', torch.norm(w).item())
2.5 忽略正则化直接训练
train(lambd=0)
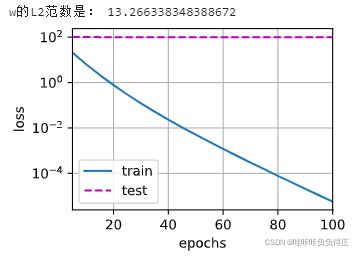
这里训练误差有了减少,但测试误差没有减少, 这意味着出现了严重的过拟合。
2.6 使用权重衰减
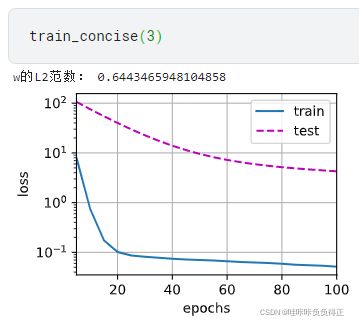
train(lambd=3)
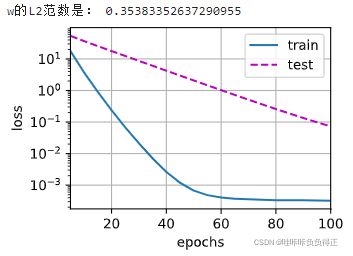
可以看到训练误差相对于无正则化的结果更大,但是测试集的误差更小。
2.7 简洁实现
我们在实例化优化器时直接通过
weight_decay指定 weight decay 超参数。 默认情况下,PyTorch 同时衰减权重和偏移。 这里我们只为权重设置了weight_decay,所以偏置参数 b b b 不会衰减。
def train_concise(wd):
net = nn.Sequential(nn.Linear(num_inputs, 1))
for param in net.parameters():
param.data.normal_()
loss = nn.MSELoss(reduction='none')
num_epochs, lr = 100, 0.003
# 偏置参数没有衰减
trainer = torch.optim.SGD([
{"params":net[0].weight,'weight_decay': wd},
{"params":net[0].bias}], lr=lr)
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
for X, y in train_iter:
trainer.zero_grad()
l = loss(net(X), y)
l.mean().backward()
trainer.step()
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1,
(d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
print('w的L2范数:', net[0].weight.norm().item())
3. Dropout
3.1 动机
一个好的模型需要对输入数据的扰动鲁棒
- 使用有噪音的数据等价于 Tikhonov 正则
- Dropout:在层之间加入噪音。
来自 B 站弹幕:意思就是输入数据加入随机扰动可以防止过拟合,泛化性更好,(数据自带的噪声可能出现偏好,加入随机噪声后,能把这种偏好抵消一点)等价于一种正则方式,现在对扰动的添加方式从输入位置放到了层间位置。
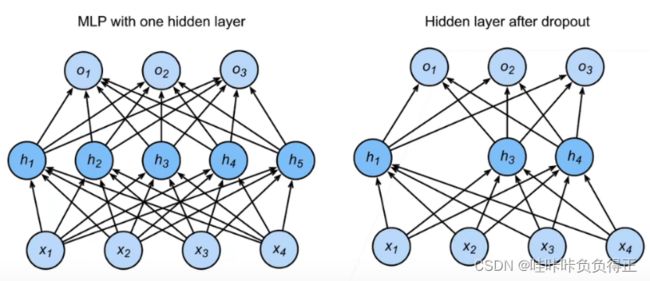
3.2 实践中的 Dropout
删除了 h 2 h_2 h2 和 h 5 h_5 h5, 因此输出的计算不再依赖于 h 2 h_2 h2 或 h 5 h_5 h5,并且它们各自的梯度在执行反向传播时也会消失。 这样,输出层的计算不能过度依赖于 h 1 , … , h 5 h_1, \ldots, h_5 h1,…,h5 的任何一个元素。
4. Dropout 代码
4.0 导入模块
#!pip install -U d2l
import torch
from torch import nn
from d2l import torch as d2l
4.1 定义 Dropout
def dropout_layer(X, dropout):
assert 0 <= dropout <= 1
# 在本情况中,所有元素都被丢弃
if dropout == 1:
return torch.zeros_like(X)
# 在本情况中,所有元素都被保留
if dropout == 0:
return X
# torch.rand(X.shape) 会产生 X.shape 形状的(0,1)的均匀分布的随机数,补充:randn 是生成标准正态分布的随机数
mask = (torch.rand(X.shape) > dropout).float()
return mask * X / (1.0 - dropout)
测试 dropout 分别为 0 0 0, 0.5 0.5 0.5, 1 1 1:
X= torch.arange(16, dtype = torch.float32).reshape((2, 8))
print(X)
print(dropout_layer(X, 0.))
print(dropout_layer(X, 0.5))
print(dropout_layer(X, 1.))
4.2 定义模型参数
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
输入为 784 = ( 28 × 28 ) 784=(28×28) 784=(28×28),输出为 10 10 10 个类别。 2 2 2 个全连接隐藏层,每个隐藏层有 256 256 256 个单元。
4.3 定义模型
# 两个隐藏层的丢弃率
dropout1, dropout2 = 0.2, 0.5
class Net(nn.Module):
def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,
is_training = True):
super(Net, self).__init__()
self.num_inputs = num_inputs
self.training = is_training
self.lin1 = nn.Linear(num_inputs, num_hiddens1)
self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
self.lin3 = nn.Linear(num_hiddens2, num_outputs)
self.relu = nn.ReLU()
def forward(self, X):
H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
# 只有在训练模型时才使用dropout
if self.training == True:
# 在第一个全连接层之后添加一个dropout层
H1 = dropout_layer(H1, dropout1)
H2 = self.relu(self.lin2(H1))
if self.training == True:
# 在第二个全连接层之后添加一个dropout层
H2 = dropout_layer(H2, dropout2)
out = self.lin3(H2)
return out
net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)
4.4 训练和测试
num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
4.5 Dropout 简洁实现
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
# 在第一个全连接层之后添加一个dropout层
nn.Dropout(dropout1),
nn.Linear(256, 256),
nn.ReLU(),
# 在第二个全连接层之后添加一个dropout层
nn.Dropout(dropout2),
nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights);
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
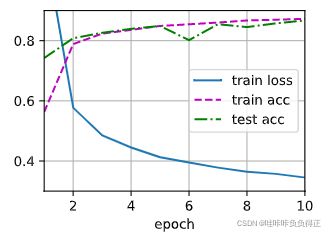
将第一层和第二层隐藏层丢失率设置为 0 0 0 情况下的结果:
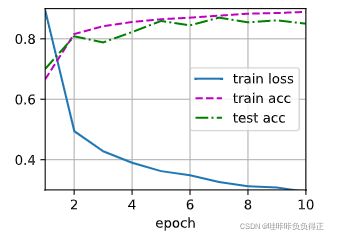
训练集精度比测试集精度稍微大一点。
4.6 李沐老师的 Q&A 补充
Dropout 操作是每一个 batch 就丢一次。
丢弃率一般设置 0.1 0.1 0.1, 0.5 0.5 0.5, 0.9 0.9 0.9。别问为什么这么设置,问就是经验。
Dropout 在训练时和在测试时的区别:
- 训练时:Dropout 随机丢弃比率 p p p 神经元,使其失效,即输出为 0 0 0。
- 测试时:全部神经元都发挥作用,但是他们的输出乘上了系数 ( 1 − p ) (1-p) (1−p)。