图片边缘检测——sobel算子、scharr算子、拉普拉斯算子、Canny边缘检测
边缘检测
- 1. 索贝尔（sobel）算子
- 2 沙尔算子
- 3 拉普拉斯算子
- 4 Canny边缘检测
1. 索贝尔（sobel）算子
-
当图片像素的某一处的颜色发生很大的改变，可以在此处进行图像的特征处理，模式识别等
-
我们人的眼睛通过对颜色的鲜艳亮度很容易判断出颜色的跃迁
-
sobel算子通过对图像求一阶导数。导数越大说明边缘信号越强！
-
由于图像都是离散的点，sobel使用离散差分算子来计算图像的近似梯度
eg:f(x)-f(x+2) 来近似计算
-
分别计算水平方向和垂直方向的近似梯度变化
+水平方向
G x G_x Gx = [ − 1 0 + 1 − 2 0 + 2 − 1 0 + 1 ] \begin{bmatrix} -1 &0&+1 \\ -2 & 0& +2 \\ -1 & 0 & +1 \end{bmatrix} ⎣⎡−1−2−1000+1+2+1⎦⎤*I -
分别卷积之后，综合考虑两个方向的梯度变化
G = G x 2 + G y 2 \sqrt{G_x^2+G_y^2} Gx2+Gy2 -
代码如下
# 索贝尔算子
import cv2
import numpy as np
img = cv2.imread('imgs/66.jpg')
# 计算X轴的梯度，只有垂直方向数据
#-1为一种数据类型，也可以使用cv2.CV_64F，ksize卷积核大小3,5都可以
dx = cv2.Sobel(img, -1, dx=1, dy=0, ksize=3)
# y轴
dy = cv2.Sobel(img, -1, dx=0, dy=1, ksize=3)
# 原图片效果
cv2.imshow('img1', img)
# x轴的效果
cv2.imshow('img2', dx)
#两个方向进行相加
dst = cv2.add(dx,dy)
#合并之后的效果
cv2.imshow('img3',dst)
cv2.waitKey(0)
2 沙尔算子
-
基本原理
索贝尔算子使用3*3的卷积核的时候，效果稍微较差。为了解决这一问题引用Scharr沙尔算子，与索贝尔算子相似，使用如下内核
G x = [ − 3 0 + 3 − 10 0 + 10 − 3 0 + 3 ] G_x = \begin{bmatrix} -3 &0&+3 \\ -10 & 0& +10 \\ -3 & 0 & +3 \end{bmatrix} Gx=⎣⎡−3−10−3000+3+10+3⎦⎤沙尔只能使用3*3的内核，所以Scharr没有kernel参数，只能求x轴ory轴的边缘索贝尔的ksize为-1 与沙尔算子功能相似
# 沙尔算子
import cv2
import numpy as np
img = cv2.imread('imgs/66.jpg')
# 计算X轴的梯度，只有垂直方向数据
dx = cv2.Scharr(img, cv2.CV_64F, dx=1, dy=0)
# y轴
dy = cv2.Scharr(img, cv2.CV_64F, dx=0, dy=1)
#两个方向进行相加
dst = cv2.addWeighted(dx,0.5,dy,0.5,0)
#合并之后的效果
cv2.imshow('img',np.hstack((img,dst)))
cv2.waitKey(0)
3 拉普拉斯算子
-
基本概念
在上述算法的基础上再次求导，以x轴为例
一阶导数： f 1 ( x ) = f ( x ) − f ( x − 1 ) f^1(x)=f(x)-f(x-1) f1(x)=f(x)−f(x−1)
二阶导数： f 2 ( x ) = f 1 ( x + 1 ) − f 1 ( x ) = ( f ( x + 1 ) − f ( x ) ) − ( f ( x ) − f ( x − 1 ) ) f^2(x)=f^1(x+1)-f^1(x)=(f(x+1)-f(x))-(f(x)-f(x-1)) f2(x)=f1(x+1)−f1(x)=(f(x+1)−f(x))−(f(x)−f(x−1))
化简后： f 2 ( x ) = f ( y − 1 ) − 2 f ( y ) + f ( y + 1 ) f^2(x)=f(y-1)-2f(y)+f(y+1) f2(x)=f(y−1)−2f(y)+f(y+1)综合x，y方向之后
f 2 ( x , y ) = [ 0 1 0 1 − 4 1 0 1 0 ] ∗ [ f ( x − 1 , y − 1 ) f ( x , y − 1 ) f ( x + 1 , y − 1 ) f ( x − 1 , y ) f ( x , y ) f ( x + 1 , y ) f ( x − 1 , y + 1 ) f ( x , y + 1 ) f ( x + 1 , y + 1 ) ] f^2(x,y)=\begin{bmatrix} 0 &1&0 \\ 1 & -4& 1 \\ 0 & 1 & 0 \end{bmatrix}*\begin{bmatrix} f(x-1,y-1) &f(x,y-1)&f(x+1,y-1) \\ f(x-1,y) & f(x,y)& f(x+1,y) \\ f(x-1,y+1) & f(x,y+1) & f(x+1,y+1) \end{bmatrix} f2(x,y)=⎣⎡0101−41010⎦⎤∗⎣⎡f(x−1,y−1)f(x−1,y)f(x−1,y+1)f(x,y−1)f(x,y)f(x,y+1)f(x+1,y−1)f(x+1,y)f(x+1,y+1)⎦⎤
# 拉普拉斯算子
import cv2
import numpy as np
img = cv2.imread('imgs/66.jpg')
dst = cv2.Laplacian(img,-1,ksize = 3)
cv2.imshow('img',np.hstack((img,dst)))
cv2.waitKey(0)
4 Canny边缘检测
- 基本概率
Canny边缘检测被誉为是最佳的边缘检测优化算法，主要由三个标准构成：
低错误率：找到真的边缘，同时减小噪音的干扰
高定位性：找到的边缘的位置与实际位置相近
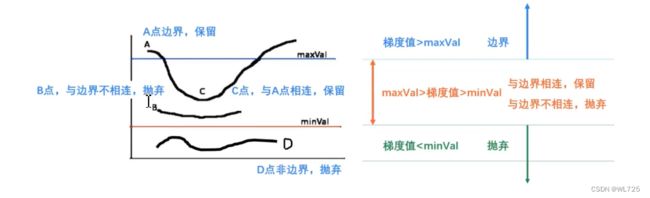
最小响应：每个边缘只标记一次 - 操作流程
- 去噪，一般使用高斯滤波进行去噪
- 计算梯度：使用sobel来计算梯度和方向，计算4个方向包括水平、垂直、两条对角线。可以计算出8个方向
- 非极大值抑制NMS：去掉所有不是边界值的点
逐个遍历像素点，判断像素点的周围有没有最大值。
假设ABC在一起，B大于A和C。那么就去掉A、C - 滞后阈值
设置一个maxValue和minValue。大于max一定是边界，小于最大值一定不是。
- 具体参数：Canny(img,minValue,maxValue)
# 拉普拉斯算子
import cv2
import numpy as np
img = cv2.imread('imgs/66.jpg')
#阈值越小越精准
std = cv2.Canny(img,64,150)
cv2.imshow('img1',img)
cv2.imshow('img2',std)
cv2.waitKey(0)