pytorch基础(六)- 卷积神经网络
目录
- 卷积介绍
- 卷积核和计算
- 卷积输出特征图可视化
- nn.Conv2d
- F.conv2d
- 池化层与采样
-
- 池化与下采样
- 上采样
- ReLU
- Batch Normalization
-
- BN计算
- nn.BatchNorm1d(in_channels)
- nn.BatchNorm2d(in_channels)
- BN的优点
- 经典卷积网络
-
- ImageNet图像分类任务
- LeNet-5 80
- AlexNet 2012
- VGG 2014
- GoogleNet 2014
- ResNet 2016
- DenseNet
- nn.Module
-
- Module嵌套
- Module容器 nn.Sequential
- Module参数管理
- Module内部的Modules管理
- Module转移
- Module参数保存和加载
- train/test状态切换
- 实现自己的类
- 数据增强
-
- 神经网络对数据的需求
- 常用数据增强方法
-
- Flip翻转
- Rotate旋转
- Scale缩放
- Copy Part裁剪一部分
- Noise添加噪声
- Random Move&Copy随机粘贴复制
- GAN生成对抗网络
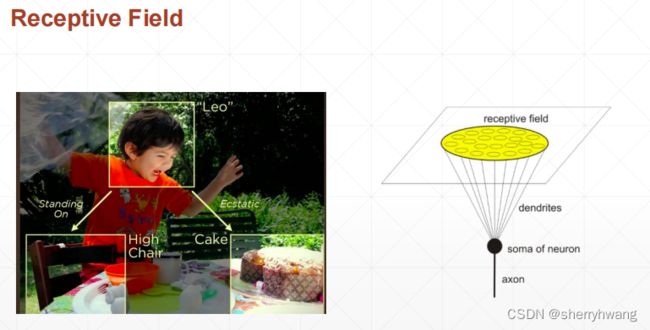
卷积介绍
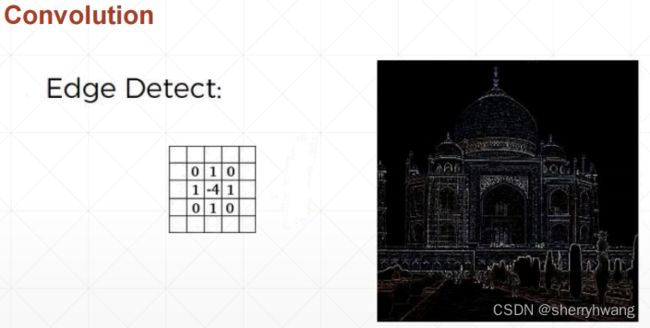
卷积核和计算
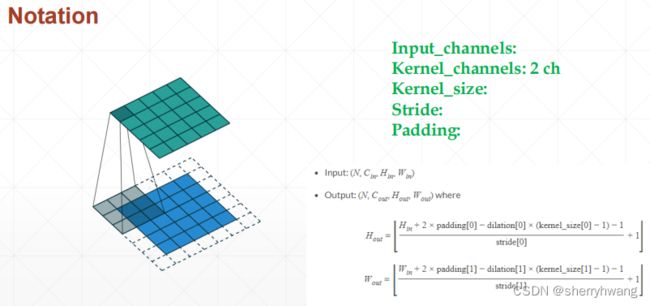
卷积输出特征图可视化
卷积神经网络低层的feature map观察的是低层的特征,比如图像中的角度、边缘之类的,中间的卷积层观察的是低维的概念,高层的卷积层关注的是更全局的概念。层层叠加卷积,逐渐提取出高维特征。

nn.Conv2d
nn.Conv2d(input_channel, output_channel, kernel_size, stride, padding)
stride:步长
import torch
import torch.nn as nn
x = torch.randn(2,1,28,28)
layer1 = nn.Conv2d(1,3, kernel_size=3, stride=1,padding=0)
layer2 = nn.Conv2d(1,3,kernel_size=3, stride=1, padding=1)
layer3 = nn.Conv2d(1,3,kernel_size=3, stride=3, padding=1)
out1 = layer1.forward(x)
out2 = layer2.forward(x)
out3 = layer3.forward(x)
out = layer1(x) #调用__call__,会调用self.forward()方法 推荐使用
print(out1.shape)
print(out2.shape)
print(out3.shape)
print(out.shape)
print(layer1.weight.shape) #weight:out_channel, in_channel, kernel_size, kernel_size
print(layer1.bias.shape) #bias: out_channel x1x1
输出:
torch.Size([2, 3, 26, 26])
torch.Size([2, 3, 28, 28])
torch.Size([2, 3, 10, 10])
torch.Size([2, 3, 26, 26])
torch.Size([3, 1, 3, 3])
torch.Size([3])
F.conv2d
pytorch命名规范,大写是类,小写是方法。
import torch
import torch.nn.functional as F
x = torch.randn(2,1,28,28)
w = torch.rand(16,1,3,3) # weight:out_channel, in_channel, kernel_size, kernel_size
b = torch.rand(16) # #bias: out_channel x1x1
out1 = F.conv2d(x, w, b, stride=1, padding=0)
out2 = F.conv2d(x, w, b, stride=1, padding=1)
out3 = F.conv2d(x, w, b, stride=2, padding=1)
print(out1.shape)
print(out2.shape)
print(out3.shape)
输出:
torch.Size([2, 16, 26, 26])
torch.Size([2, 16, 28, 28])
torch.Size([2, 16, 14, 14])
池化层与采样
池化与下采样
subsample:是隔行采样;
pooling:在窗口内做最大/平均计算,或其它计算;
最大池化:
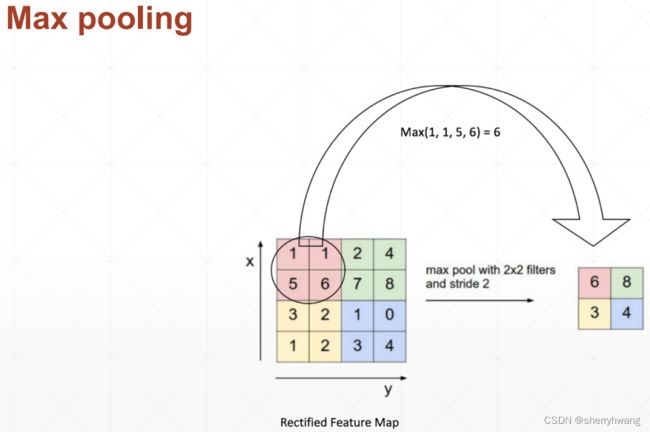
平均池化:
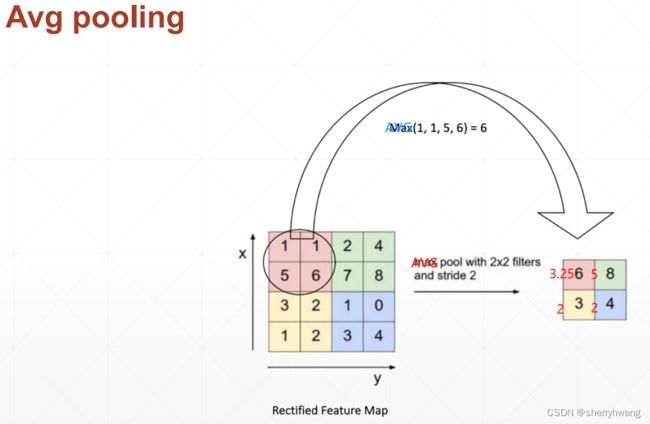
池化的作用:
- 减少feature map的大小
代码:
import torch
import torch.nn as nn
import torch.nn.functional as F
x = torch.randn(2,1,28,28)
layer1 = nn.MaxPool2d(2, stride=2)
layer2 = nn.AvgPool2d(2, stride=2)
out1 = layer1(x)
out2 = layer2(x)
print(out1.shape)
print(out2.shape)
out3 = F.max_pool2d(x, kernel_size = 2, stride = 2)
out4 = F.avg_pool2d(x, kernel_size = 2, stride = 2)
print(out3.shape)
print(out4.shape)
输出:
torch.Size([2, 1, 14, 14])
torch.Size([2, 1, 14, 14])
torch.Size([2, 1, 14, 14])
torch.Size([2, 1, 14, 14])
上采样
向上采样-upsample:
处理Tensor类型数据,对其进行上采样;
F.interpolate(x, scale_factor, mode)
mode: 插值的模式
import torch
import torch.nn as nn
import torch.nn.functional as F
x = torch.randn(2,1,5,5)
out1 = F.interpolate(x, scale_factor=2, mode='nearest')
out2 = F.interpolate(x, scale_factor=3, mode='nearest')
print(out1.shape)
print(out2.shape)
输出:
torch.Size([2, 1, 10, 10])
torch.Size([2, 1, 15, 15])
ReLU
卷积神经网络基本的unit一般包含:
conv2d->BN-> Pool->ReLU,BN、Pool、ReLU三种顺序没有主流的选择,按照心得或者任务选择。
import torch
import torch.nn as nn
import torch.nn.functional as F
x = torch.randn(2,1,5,5)
layer = nn.ReLU(inplace=True)
out1 = layer(x)
out2 = F.relu(x, inplace=True)
print(out1.shape)
print(out2.shape)
输出:
torch.Size([2, 1, 5, 5])
torch.Size([2, 1, 5, 5])
Batch Normalization
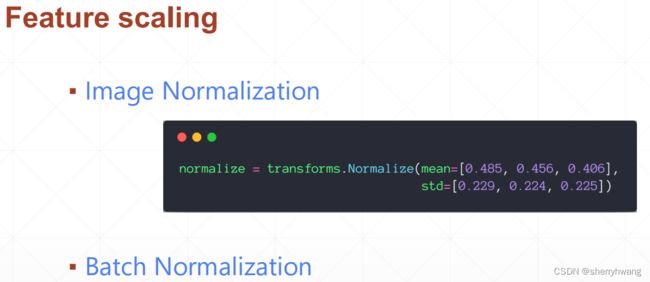
在使用sigmoid函数的情况下,会出现梯度弥散的现象,导致参数迟迟得不到更新。虽然这种情况可以通过ReLU函数得到缓解,但是有些情况下必须使用sigmoid激活函数。所以需要一个方法将数据转换到一个有效的的区间内。BN将数据转换为以0为均值,方差较小的分布,也叫Feature scaling.
BN作用激活函数输入之前的数据。


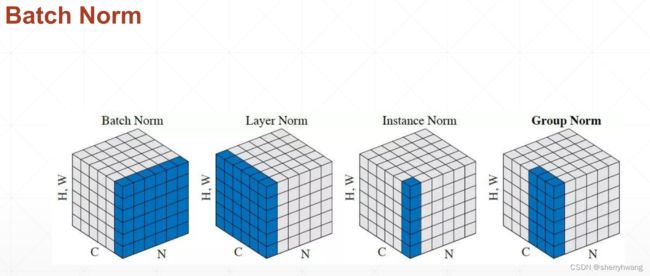
Batch Norm:对每一个通道上的(N,HW)数据做归一化,均值和方差的shape为[C]
Layer Norm:对每一个实例的(C,HW)数据做归一化,均值和方差的shape为[N]
Instance Norm:对每一个实例的每一个(HW)数据做归一化,均值和方差的shape为[C,N]
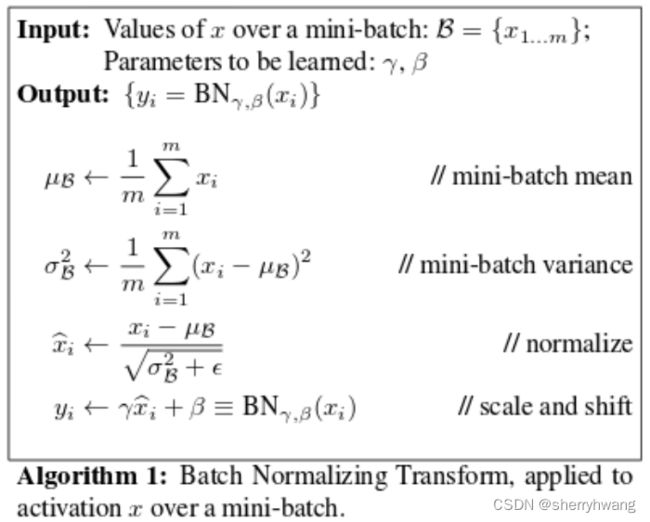
BN计算
每个channel上的数据,减去这个channels上统计得到的均值,除以这个channels上统计得到的方差,使其逼近与0-1正态分布。再加上 γ \gamma γ和 β \beta β得到 γ \gamma γ- β \beta β的正态分布。 γ \gamma γ和 β \beta β是可学习的,是需要梯度信息的。
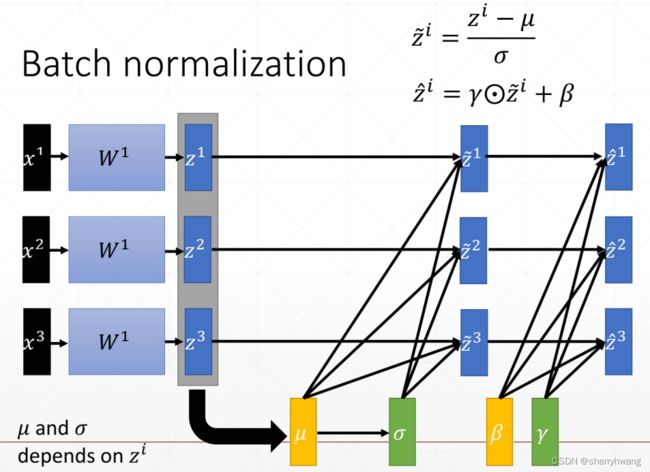
(这里 μ \mu μ和 σ \sigma σ和 z i z^i zi形状为[C],C为通道数)
nn.BatchNorm1d(in_channels)
nn.BatchNorm1d.running_mean代表当前batch的均值;
nn.BatchNorm1d.running_var代表当前batch的方差;
nn.BatchNorm1d.weight代表 γ \gamma γ;
nn.BatchNorm1d.bias代表 β \beta β;
import torch
import torch.nn as nn
import torch.nn.functional as F
x = torch.randn(10,16,784) # b,channels,Hw
layer = nn.BatchNorm1d(16) #channels
out = layer(x)
print(layer.running_mean)
print(layer.running_var)
输出:
tensor([-0.0004, 0.0008, 0.0012, 0.0005, -0.0004, -0.0002, 0.0022, -0.0008,
0.0015, 0.0004, 0.0003, -0.0002, 0.0006, -0.0022, 0.0014, 0.0003])
tensor([1.0006, 0.9976, 0.9995, 0.9994, 0.9999, 1.0003, 0.9987, 1.0002, 1.0002,
1.0013, 0.9999, 1.0033, 0.9980, 0.9984, 1.0010, 0.9991])
nn.BatchNorm2d(in_channels)
import torch
import torch.nn as nn
import torch.nn.functional as F
x = torch.randn(10,16,28,28)
layer = nn.BatchNorm2d(16)
out = layer(x)
print(layer.running_mean.shape)
print(layer.running_var.shape)
print(layer.weight.shape)
print(layer.bias.shape)
print(vars(layer))
输出:
torch.Size([16])
torch.Size([16])
torch.Size([16])
torch.Size([16])
{'training': True, '_parameters': OrderedDict([('weight', Parameter containing:
tensor([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
requires_grad=True)), ('bias', Parameter containing:
tensor([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
requires_grad=True))]), '_buffers': OrderedDict([('running_mean', tensor([ 1.8079e-03, -2.5026e-04, -1.4939e-03, -6.3105e-04, 6.8191e-04,
1.0124e-04, -2.2681e-03, 2.3068e-03, 8.3116e-04, -1.3128e-03,
-2.1227e-05, 3.3749e-04, 2.6776e-03, 8.1243e-04, 1.2933e-03,
-5.1558e-04])), ('running_var', tensor([0.9990, 1.0008, 1.0006, 0.9975, 1.0025, 0.9980, 1.0019, 1.0009, 1.0009,
1.0007, 0.9982, 1.0010, 1.0012, 1.0017, 1.0007, 1.0021])), ('num_batches_tracked', tensor(1))]), '_non_persistent_buffers_set': set(), '_backward_hooks': OrderedDict(), '_is_full_backward_hook': None, '_forward_hooks': OrderedDict(), '_forward_pre_hooks': OrderedDict(), '_state_dict_hooks': OrderedDict(), '_load_state_dict_pre_hooks': OrderedDict(), '_modules': OrderedDict(), 'num_features': 16, 'eps': 1e-05, 'momentum': 0.1, 'affine': True, 'track_running_stats': True}
BN的优点

因为BN不在使数据的容易出现在sigmoid激活函数的饱和区,所以梯度更新更快,能够更快的收敛;
训练更稳定,可以使用更大范围的学习率,使得学习率的调整不再那么敏感了;

经典卷积网络
ImageNet图像分类任务
2012年AlexNet使用深度学习将ImageNet图像分类任务错误率降低到16.4,使得学术界开始关注深度学习;

LeNet-5 80
80年代卷积神经网络的发明,用于手写数字识别;但是基于当时的计算能力,这个网络结构比较小,当时没有GPU;
2convs + 3fc 一共五层;

AlexNet 2012
2012年AlexNet在ImageNet数据集上取得了10%+准确率的提升,2012年ImageNet图像识别的冠军;
一共有8层 5convs+3fc;
在2块 GTX580上训练的,使用两组卷积参数,再合并输出。
创新:使用Pooling操作;引用ReLU,引入Dropout;
VGG 2014
牛津大学视觉研究组,发明了6种网络结构;2014年ImageNet图像识别挑战赛第2名;
创新:使用堆叠的小尺度卷积核替代大的卷积核,不会损失精度,而计算更快;
11-19层,网络层数比AlexNet更深。
GoogleNet 2014
2014年ImageNet图像识别挑战赛第1名;
一共22层,比VGG层数更深;
对同一层,使用多个不同类型的卷积核,


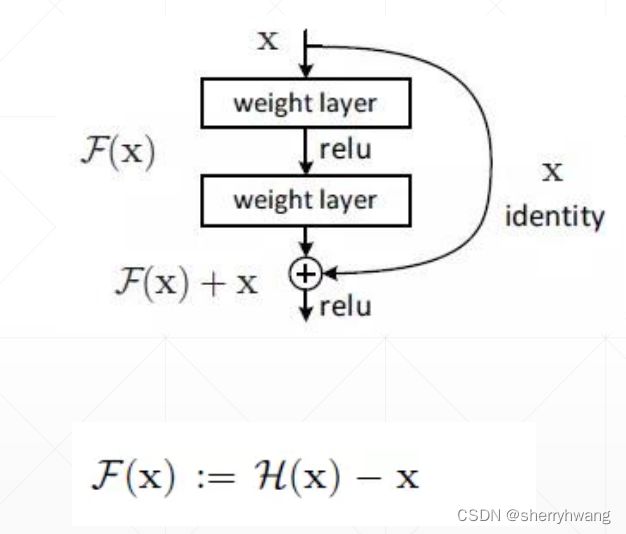
ResNet 2016
深度残差网络。
单纯地堆叠网络层并不会使得网络的性能得到提升,因为随着网络深度加深,会存在梯度消失/梯度弥散的情况,使得网络参数得不到更新。
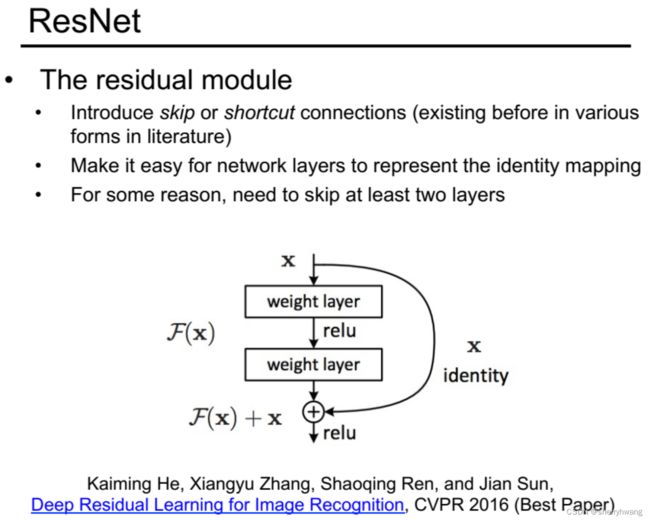
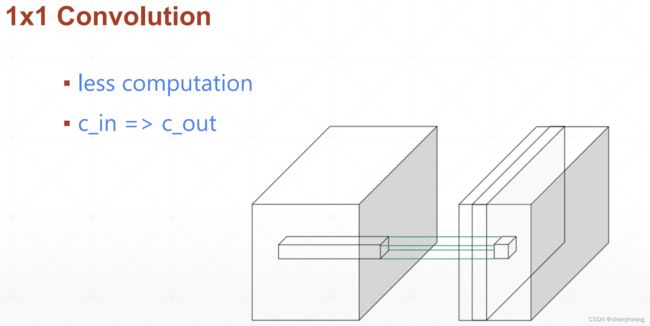
每一个残差单元的结构,可以不是单纯的堆叠多个3x3卷积,而是先通过1x1卷积降低特征图通道数,然后使用3x3卷积,最后使用1x1卷积将特征图通道数转换为残差输入的特征通道数,这样就减少了计算量,使得堆叠更深的网络成为了可能。


DenseNet
不同卷积层之间的连接变得非常密集。连接方式采用concate操作。

nn.Module
所有网络层类的父类。如果要实现自定义的网络,则必须继承这个类。

Module嵌套
Module容器 nn.Sequential
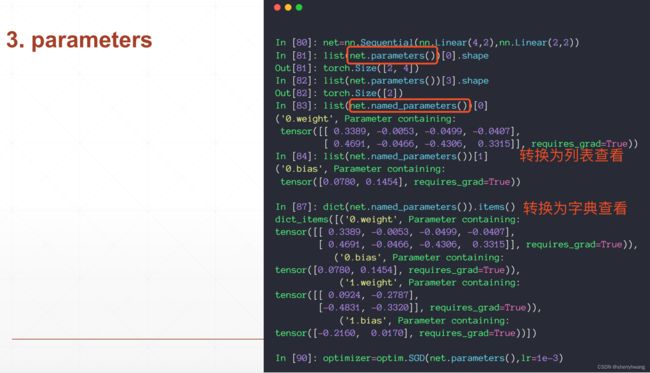
Module参数管理
参数管理:
方法
net.parameters()
net.named_parameters()
import torch
import torch.nn as nn
import torch.nn.functional as F
net = nn.Sequential(
nn.Linear(2,4),
nn.Linear(4,1),
nn.ReLU(inplace=True)
)
print(list(net.parameters())[0].shape)
print(list(net.parameters())[1].shape)
print(list(net.parameters())[2].shape)
print(list(net.parameters())[3].shape)
print(list(net.parameters())[0])
print('*'*20)
print(list(net.named_parameters())[0])
print('*'*20)
print(dict(net.named_parameters()).items())
输出:
torch.Size([4, 2])
torch.Size([4])
torch.Size([1, 4])
torch.Size([1])
Parameter containing:
tensor([[-0.6702, 0.1455],
[-0.4835, -0.2833],
[-0.2023, 0.0137],
[ 0.4649, -0.5334]], requires_grad=True)
********************
('0.weight', Parameter containing:
tensor([[-0.6702, 0.1455],
[-0.4835, -0.2833],
[-0.2023, 0.0137],
[ 0.4649, -0.5334]], requires_grad=True))
********************
dict_items([('0.weight', Parameter containing:
tensor([[-0.6702, 0.1455],
[-0.4835, -0.2833],
[-0.2023, 0.0137],
[ 0.4649, -0.5334]], requires_grad=True)), ('0.bias', Parameter containing:
tensor([-0.2524, 0.2499, -0.4449, 0.3388], requires_grad=True)), ('1.weight', Parameter containing:
tensor([[-0.4255, 0.2373, 0.2126, 0.1588]], requires_grad=True)), ('1.bias', Parameter containing:
tensor([0.4015], requires_grad=True))])
Module内部的Modules管理
module内部的modules管理:
方法
net.modules() 所有的(包含子嵌套的)modules.
net.children() 直接嵌套(不包含子嵌套)的modules.
from re import L
from turtle import forward
import torch
import torch.nn as nn
import torch.nn.functional as F
class MyModule(nn.Module):
def __init__(self):
super().__init__()
self.net = nn.Linear(4,3)
def forward(self, x):
return self.net(x)
class Net(nn.Module):
def __init__(self):
super().__init__()
self.net = nn.Sequential(
MyModule(),
nn.ReLU(inplace=True),
nn.Linear(3, 2)
)
def forward(self, x):
return self.net(x)
model = Net()
# print(dict(model.named_parameters()).items())
print('modules........')
print(list(model.modules()))
print(len(list(model.modules())))
print('children.......')
print(list(model.children()))
print(len(list(model.children())))
输出:
modules........
[Net(
(net): Sequential(
(0): MyModule(
(net): Linear(in_features=4, out_features=3, bias=True)
)
(1): ReLU(inplace=True)
(2): Linear(in_features=3, out_features=2, bias=True)
)
), Sequential(
(0): MyModule(
(net): Linear(in_features=4, out_features=3, bias=True)
)
(1): ReLU(inplace=True)
(2): Linear(in_features=3, out_features=2, bias=True)
), MyModule(
(net): Linear(in_features=4, out_features=3, bias=True)
), Linear(in_features=4, out_features=3, bias=True), ReLU(inplace=True), Linear(in_features=3, out_features=2, bias=True)]
6
children.......
[Sequential(
(0): MyModule(
(net): Linear(in_features=4, out_features=3, bias=True)
)
(1): ReLU(inplace=True)
(2): Linear(in_features=3, out_features=2, bias=True)
)]
1
Module转移
Module参数保存和加载
torch.load将参数保存的文件转换为pytorch定义的类,

train/test状态切换
对于dropout或者BN层来说,训练和测试时的行为是不一样的,所以模型存在train和test两种状态。

实现自己的类
继承于nn.Module实现自己的模型/网络层。
pytorch不存在faltten操作的类,可以继承nn.Module自定义。

自定义线性层:
nn.Parameter()自定义的参数会由nn.parameters()这个方法返回,并且设置了梯度,从而被优化器优化。

数据增强
神经网络对数据的需求
随着网络层数加深,参数量增加,网络表达能力增强,就需要大量数据使得网络不容易过拟合。

在有限数据下,解决神经网络对数据的需求,使得网络得到很好的训练(优化)的方法:
- 减少网络的参数量;
- 在网络结构固定的情况下,使用正则化方法;
- 数据增强;

数据增强可以帮助提升网络性能,但是得到的数据分布与原始数据的分布相差无几,所以数据增强可以提升网络性能,但不会提升太多。

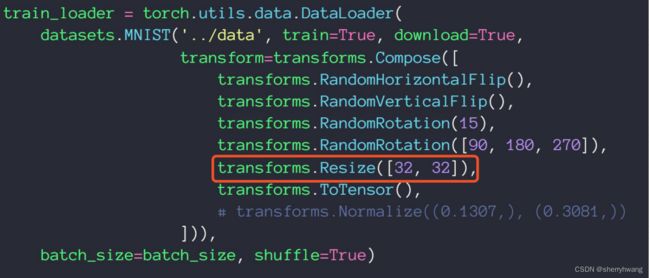
常用数据增强方法
Flip翻转
水平方向和垂直方向的翻转;

每一个样本做一个随机水平或者垂直翻转,随机指的是可能做,可能不做;

Rotate旋转
Scale缩放
Copy Part裁剪一部分
随机裁剪出一部分;如下图的剪裁红框或者绿框部分;随机裁剪用得比较多。

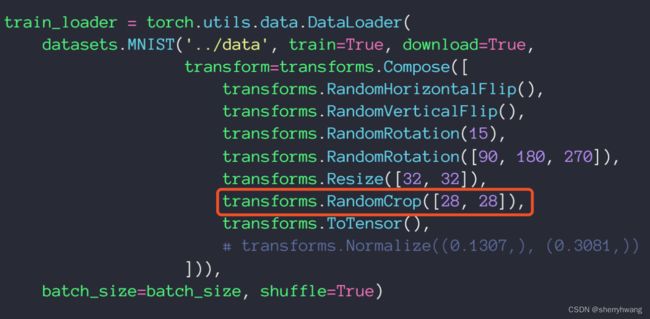
Noise添加噪声
添加一些高斯噪声;在numpy数据上添加。或者torch的高斯分布数据叠加到图像tensor上去。