简单理解图神经网络 GNN
简单理解图神经网络 GNN
前言
图神经网络(Graph Neural Networks,GNN)最早由The Graph Neural Network Model(Gori et al., 2005)提出。近年来,深度学习领域关于图神经网络的研究热情日益高涨,图神经网络已经成为各大深度学习顶会的研究热点。
本文主要介绍图神经网络的基本原理,通过简单的方式理解 GNN, GCN 是如何工作的,尽量把原理说清楚。
Overview
总的来说,GNN 就是做了这么一件事情:利用图的节点信息去生成节点(图)的 Embedding 表示。
Graph Neural Network(GNN)
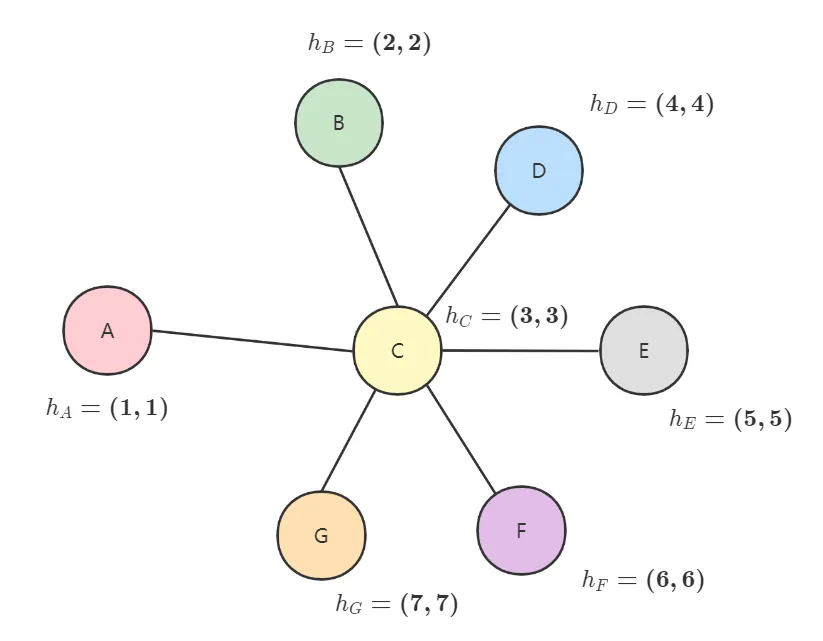
既然是 Graph,那么我们的数据就是一张图:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lMlA3L6x-1656760016934)(https://static.emoryhuang.cn/webp/656651309-gnn-0.webp)]
其中 h A , h B , h C , h D , h E h_A, h_B, h_C, h_D, h_E hA,hB,hC,hD,hE分别是节点 A , B , C , D , E A, B, C, D, E A,B,C,D,E的所包含的信息,你也可以简单理解为是这个节点的特征。
GNN 可分为三步:1. 聚合;2. 更新;3. 循环。
首先是聚合。通过观察上面的图我们可以发现,节点 A A A有三个邻居节点 B , C , D B,C,D B,C,D,显然这是一个非常重要的信息,节点 A A A与这三个节点有密切的联系。举个例子,如果我们不知道节点 A A A是否有钱,但是我们发现节点 B , C , D B,C,D B,C,D都非常有钱,那么很大程度上节点 A A A也非常有钱,也就是通过节点的邻居信息判断这个节点的信息。那么要如何利用这个特征呢?
就像在一开始说的,GNN 就是利用图的节点信息去生成节点(图)的 Embedding 表示,这也就是聚合。我们可以通过简单的方式获取邻居的信息:
N A = a ⋅ h B + b ⋅ h C + c ⋅ h D = a ⋅ ( 2 , 2 ) + b ⋅ ( 3 , 3 ) + c ⋅ ( 4 , 4 ) \begin{aligned}N_A &= a \cdot h_B + b \cdot h_C + c \cdot h_D \\ &= a \cdot (2,2) + b \cdot (3,3) + c \cdot (4,4) \end{aligned} NA=a⋅hB+b⋅hC+c⋅hD=a⋅(2,2)+b⋅(3,3)+c⋅(4,4)
其中 a , b , c a,b,c a,b,c为常数,也可以通过训练得到或者是手动设定,我们这里简单理解为常数。
好了,通过上面的简单的方式,我们得到了节点 A A A的邻居的信息,我们将这个信息作为节点 A A A信息的补充。
再来是更新。当我们获取了邻居的信息后,自然也不能忘了节点 A A A本身的信息:
( h A + α ⋅ N A ) (h_A + \alpha \cdot N_A) (hA+α⋅NA)
其中 α \alpha α为常数(同样也可以通过训练得到或者是手动设定,这里简单理解为常数)。当然了,肯定不能直接简单加起来就作为节点 A A A的新的信息,而是需要进行一些处理,其实也就是常规的线性变换,再过个激活函数:
h A = σ ( W ( h A + α ⋅ N A ) ) \begin{aligned}h_A = \sigma (W (h_A + \alpha \cdot N_A)) \end{aligned} hA=σ(W(hA+α⋅NA))
其中 σ \sigma σ为激活函数, W W W为权重矩阵, h A h_A hA为节点 A A A的信息, N A N_A NA为节点 A A A的邻居信息。
简而言之,聚合更新就是把节点的邻居的信息添加到这个节点中。
现在,一次聚合操作就完成了,经过一次聚合之后:
- 节点 A A A中有 B , C , D B,C,D B,C,D的信息;
- 节点 B B B中有 A , C A,C A,C的信息;
- 节点 C C C中有 A , B , D , E A,B,D,E A,B,D,E的信息;
- 节点 D D D中有 A , C A,C A,C的信息;
- 节点 E E E中有 C C C的信息;
第二次聚合也是类似的,仍然以节点 A A A为例,计算节点 A A A的邻居信息。但此时当节点 A A A聚合节点 C C C的时候,由于节点 C C C中包含了节点 E E E的信息,所以这时节点 A A A获得了二阶邻居 E E E的信息。
归根结底,GNN 就是一个提取特征的方法。
Graph Convolutional Network(GCN)
好了,讲完了 GNN 的总体思路,让我们具体来看看 GCN 是怎么做的。还是以下面这幅图为例:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ra79qoOy-1656760016935)(https://static.emoryhuang.cn/webp/656651309-gnn-0.webp)]
同样的,我们需要获取节点 A A A的邻居信息:
N A = a ⋅ h B + b ⋅ h C + c ⋅ h D = a ⋅ ( 2 , 2 ) + b ⋅ ( 3 , 3 ) + c ⋅ ( 4 , 4 ) \begin{aligned}N_A &= a \cdot h_B + b \cdot h_C + c \cdot h_D \\ &= a \cdot (2,2) + b \cdot (3,3) + c \cdot (4,4) \end{aligned} NA=a⋅hB+b⋅hC+c⋅hD=a⋅(2,2)+b⋅(3,3)+c⋅(4,4)
这里我们使用矩阵的方式来表示图,邻接矩阵 A A A,以及隐藏层矩阵 H H H。
A = [ 0 1 1 1 0 1 0 1 0 0 1 1 0 1 1 1 0 1 0 0 0 0 1 0 0 ] H = [ 1 1 2 2 3 3 4 4 5 5 ] A = \begin{bmatrix} 0 & 1 & 1 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 \\ 1 & 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \end{bmatrix} \quad H = \begin{bmatrix} 1 & 1 \\ 2 & 2 \\ 3 & 3 \\ 4 & 4 \\ 5 & 5 \end{bmatrix} A=⎣⎢⎢⎢⎢⎡0111010100110111010000100⎦⎥⎥⎥⎥⎤H=⎣⎢⎢⎢⎢⎡1234512345⎦⎥⎥⎥⎥⎤
这里假设 a = b = c = 1 a=b=c=1 a=b=c=1,那么,节点 A A A的邻居信息就可以表示为:
$$
\begin{aligned}
N_A &= \begin{bmatrix} 0 & 1 & 1 & 1 & 0 \end{bmatrix}
\begin{bmatrix}
1 & 1 \
2 & 2 \
3 & 3 \
4 & 4 \
5 & 5
\end{bmatrix}
\begin{bmatrix}9 & 9\end{bmatrix} \
&= A_{0,*}H
\end{aligned}
$$
其中 A 0 , ∗ A_{0,*} A0,∗表示矩阵 A A A的第一行,即节点 A A A的邻居关系。另外别忘了加上节点 A A A自身的信息,具体来说,可以通通过加上单位矩阵 I I I的方式实现:
$$
\begin{aligned}
N_A &= \left( \begin{bmatrix} 0 & 1 & 1 & 1 & 0 \end{bmatrix} +
\begin{bmatrix} 1 & 0 & 0 & 0 & 0 \end{bmatrix}\right)
\begin{bmatrix}
1 & 1 \
2 & 2 \
3 & 3 \
4 & 4 \
5 & 5
\end{bmatrix}
\begin{bmatrix}10 & 10\end{bmatrix} \
&= (A_{0,} + I_{0,})H
\end{aligned}
$$
同理,我们可以得到所有节点的邻居信息 N N N:
N = ( A + I ) H : = A ~ H \begin{aligned}N &= (A + I)H \\ &:= \tilde{A}H \end{aligned} N=(A+I)H:=A~H
记 A ~ = A + I \tilde{A} = A + I A~=A+I
现在,就可以写出隐藏层的更新方程了,与之前的思路类似,常规的线性变换,再过个激活函数:
H ( l + 1 ) = σ ( A ~ H ( l ) W ( l ) ) H^{(l+1)} = \sigma (\tilde{A}H^{(l)}W^{(l)}) H(l+1)=σ(A~H(l)W(l))
其中 l l l为循环层数, σ \sigma σ为激活函数, W W W为隐藏层的权重矩阵。
现在还有最后一个问题,你会发现,原本节点 A A A的信息是 ( 1 , 1 ) (1,1) (1,1),经过聚合之后变成 ( 10 , 10 ) (10,10) (10,10),可以想象的是它会越来越「膨胀」。
实际上,解决这个问题并不麻烦,归一化就行了。在图 Graph 中,我们可以借助「度」来进行归一化。具体为什么这么做、为什么要进行归一化我们放在后面讲:关于归一化的一些问题。
具体什么是度这里就不赘述了,给出度矩阵:
D = [ 3 0 0 0 0 0 2 0 0 0 0 0 4 0 0 0 0 0 2 0 0 0 0 0 1 ] D ~ = [ 4 0 0 0 0 0 3 0 0 0 0 0 5 0 0 0 0 0 3 0 0 0 0 0 2 ] D = \begin{bmatrix} 3 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 \\ 0 & 0 & 4 & 0 & 0 \\ 0 & 0 & 0 & 2 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix} \quad \tilde{D} = \begin{bmatrix} 4 & 0 & 0 & 0 & 0 \\ 0 & 3 & 0 & 0 & 0 \\ 0 & 0 & 5 & 0 & 0 \\ 0 & 0 & 0 & 3 & 0 \\ 0 & 0 & 0 & 0 & 2 \end{bmatrix} D=⎣⎢⎢⎢⎢⎡3000002000004000002000001⎦⎥⎥⎥⎥⎤D~=⎣⎢⎢⎢⎢⎡4000003000005000003000002⎦⎥⎥⎥⎥⎤
其中, D , D ~ D,\tilde{D} D,D~分别是 A , A ~ A,\tilde{A} A,A~的度矩阵。
这里直接给出 GCN 论文 Semi-Supervised Classification with Graph Convolutional Networks 中的归一化方法,它的本质是正则化的拉普拉斯矩阵:
D ~ − 1 / 2 A ~ D ~ − 1 / 2 \tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2} D~−1/2A~D~−1/2
关于上面的归一化方法,我们同样在后面具体讨论:关于归一化的一些问题,如果你不想了解细节也没关系,你只需要知道它的作用即可。
至此为止,我们可以得到完整的隐藏层的更新方程:
H ( l + 1 ) = σ ( D ~ − 1 / 2 A ~ D ~ − 1 / 2 H ( l ) W ( l ) ) H^{(l+1)} = \sigma (\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}H^{(l)}W^{(l)}) H(l+1)=σ(D~−1/2A~D~−1/2H(l)W(l))
其中 l l l为循环层数, σ \sigma σ为激活函数, W W W为隐藏层的权重矩阵, A ~ = ( A + I ) \tilde{A} = (A + I) A~=(A+I), D ~ \tilde{D} D~是 A ~ \tilde{A} A~的度矩阵。虽然式子长得难看了点,但我想如果你了解了上面讲的内容,也就不难理解了。
关于归一化的一些问题
下班了,下班了,下周再写…
Graph Attention Network(GAT)
如果你熟悉 Attention 机制,那么在了解了上面的内容之后,就不难理解 Graph Attention Network(GAT) 了,无非就是对邻居节点的权重进行自动学习,这里就不再细说了。
总结
最后,还是想强调一点,GNN 就是做了这么一件事情:利用图的节点信息去生成节点(图)的 Embedding 表示。就是那么一个 Embedding 的方法。
参考资料
- [1] The Graph Neural Network Model
- [2] Semi-Supervised Classification with Graph Convolutional Networks
- 简单粗暴带你快速理解 GNN
- 图卷积网络(GCN)入门详解