算法系列—红黑树（C++实现）
红黑树（Red-Black Tree）是二叉搜索树（Binary Search Tree）的一种改进。二叉查找树在最坏情况下可能会变成一个链表（从小到大插入时）。而红黑书每次插入或删除后都会用O(logN)的时间来修改树的结构以保持平衡。红黑树另一个优点是：除了删除和插入以外，二叉查找树中的查找最大键，查找最小键，查找小于当前键的元素数量，查找某一个键 等算法不用任何修改就可以直接在红黑树中使用。
红黑树的结点额外添加了一个属性为：颜色，分为红色和黑色。可以认为红色结点与其父结点（黑色）可以构成一颗3-树（即有两个键和三条链接的树）。
----------------------------------
引言：
作者本来想实现一下红黑树，网上搜了以后发现了一篇不错的文章http://blog.csdn.net/v_JULY_v/article/details/6109153
但是作者在“红黑树的插入和删除结点的全程演示”中所用到的方法和实现与剖析中所用到的方法并不一样。
而我找到了一种更简单的删除算法：http://gengning938.blog.163.com/blog/static/1282253812011420103852696/
但是此处只有图片和文字，没有代码实现，于是打算结合两者的优点，代码主体使用的是v_JULY_v的，但是删除算法用的是枫叶大哥的。
----------------------------------
正文：
红黑树的四条性质：
1：根结点是黑色的。
2：空结点是黑色的。
3：一条连接不能同时链接两个红色结点。
4：从根节点到任何外部节点（叶子节点）路径上经过的黑色结点数目是相同的。
而这些性质约束了红黑树从根到叶子节点的路径最多不超过最短可能路径的两倍长。因为红黑树不是绝对平衡的，但可以认为是黑色绝对平衡的。
将红色结点与其父结点之间的链接画平，可以直观看出上述结论。
由于删除和插入都要用到一种叫做左旋和右旋的方法，所以我们先介绍一下左旋和右旋：
如上图是以x为枢轴点左旋（从左图->右图）和以y轴为枢轴点右旋（右图->左图）。
实现比较简单：右旋为例：
y的左链接指向β，x的又链接指向y，y的父链接的左或者右（取决于y在哪边）链接指向x。
左旋的话，上述左和右颠倒就可以。
左旋、右旋都是对称的，且都是在O（1）时间内完成。因为旋转时只有指针被改变。
红黑树的插入算法实现：
插入首先是按部就班二叉搜索树的插入步骤，把新节点z插入到某一个叶节点的位置上。
接下来把z的颜色设成红色。为什么？还记得红黑树的性质吗，从根节点向下到空节点的每一条路径上的黑色节点数要相同。如果新插入的是黑色节点，那么它所在的路径上就多出了一个黑色的节点了。所以新插入的节点一定要设成红色。但是这样可能又有一个矛盾，如果z的父节点也是红色，怎么办，前面说过红色节点的子节点必须是黑色。因此我们要执行下面一个迭代的过程，称为InsertFixup，来修补这棵红黑树。
接下来把z的颜色设成红色。为什么？还记得红黑树的性质吗，从根节点向下到空节点的每一条路径上的黑色节点数要相同。如果新插入的是黑色节点，那么它所在的路径上就多出了一个黑色的节点了。所以新插入的节点一定要设成红色。但是这样可能又有一个矛盾，如果z的父节点也是红色，怎么办，前面说过红色节点的子节点必须是黑色。因此我们要执行下面一个迭代的过程，称为InsertFixup，来修补这棵红黑树。
InsertFixup有三种情况：
情况1
如果叔叔结点为红色。
下图为插入N节点的情况。
转换前：
转换后：
上图中将情况1转换为了情况2.
情况2：
叔叔节点为黑色：插入节点是父结点的右孩子。
继续上图的转换，转换后：
这时情况2转换为了情况3：
情况3
叔叔节点为黑色：插入节点为左孩子。
三种情况的具体实现在源代码中有充分解释，代码中注释的ABCDEFG标识对应着各种情况的代码实现。
红黑树的删除：
原文：http://gengning938.blog.163.com/blog/static/1282253812011420103852696/
感谢枫叶大哥提供了这么简单的方法。
这里对不全的地方做了一些修改（原文中添加了几处，以及添加了隐藏知识点）。
一些隐藏知识点：
遇到节点先判断是否有两个子结点，如果有就查找右子树中最小值进行替换。没有两个子结点就跳过替换。
经过上一步以后，要删除的点变为以下情况：
不可能还有两个子节点。
如果有一个子结点的话，那么该节点肯定为右结点，且要删除的节点肯定为黑色，而右结点肯定为红色。
如果无子节点的话，则删除结点可能为红色，可能为黑色。
删除结点首先要按二叉查找树删除结点的算法进行
一、普通二叉查找树删除一个结点：
(1)待删除结点没有子结点，即它是一个叶子结点，此时直接删除
(2)待删除结点只有一个子结点，则可以直接删除；如果待删除结点是根结点，则它的子结点变为根结点；如果待删除结点不是根结点，则用它的子结点替代它的位置。
(3)待删除结点有两个子结点，首先找出该结点的后继结点（即右子树中数值最小的那个结点），然后将两个结点进行值交换（即：只交换两个结点的数值，不改变结点的颜色）并将待删除结点删除，由于后继结点不可能有左子结点，对调后的待删除结点也不会有左子结点，因此要把它删除的操作会落入情况（1）或情况（2）中。
二、.红黑树的删除结点算法
1.待删除结点有两个外部结点，操作如下：
（1）直接把该结点调整为叶结点
（2）若该结点是红色，则可直接删除，不影响红黑树的性质，算法结束
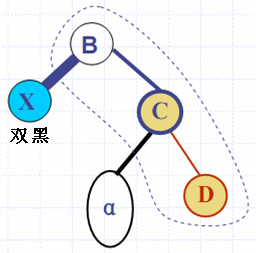
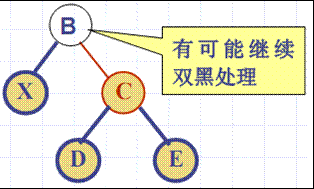
（3）若该结点是黑色，则删除后红黑树不平衡。此时要进行“双黑”操作
记该结点为V，则删除了V后，从根结点到V的所有子孙叶结点的路径将会比树中其他的从根结点到叶结点的路径拥有更少的黑色结点， 破坏了红黑树性质4。此时，用“双黑”结点来表示从根结点到这个“双黑”结点的所有子孙叶结点的路径上都缺少一个黑色结点。
双黑含义：该结点需要代表两个黑色结点，才能维持树的平衡
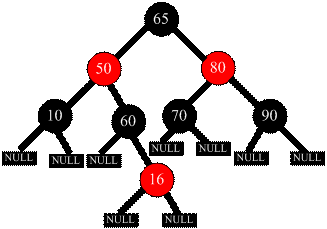
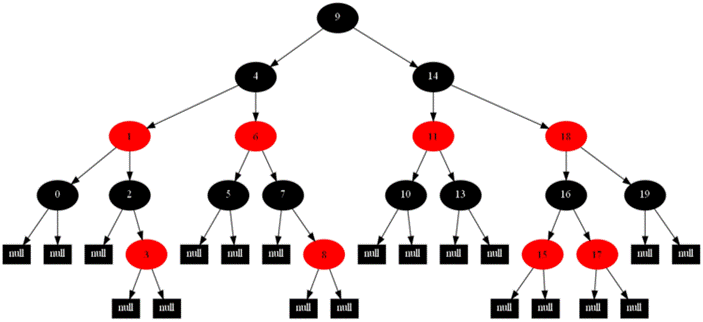
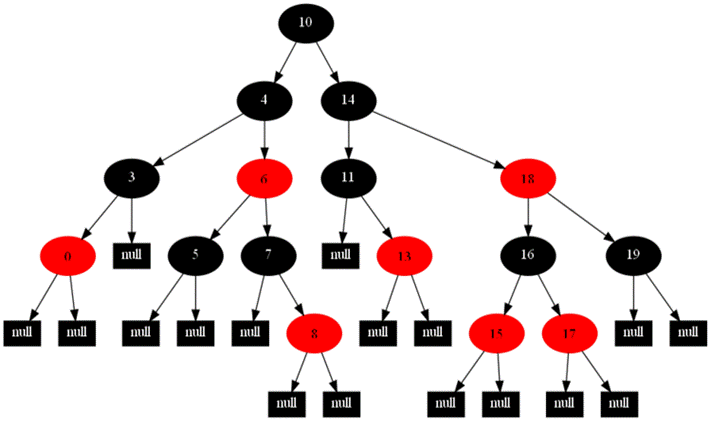
图1
如图1，要删除结点90，则删除后从根结点到结点90的所有子树结点的路径上的黑色结点比从根点到叶结点的路径上的黑结点少。因而，删除结点90后，用子结点NULL代替90结点，并置为“双黑”结点。
2. 待删除结点有一个外部结点，操作为：
该节点是黑色，其非空子节点为红色 ；则将其子节点提升到该结点位置，颜色变黑
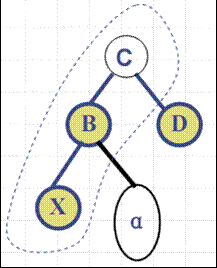
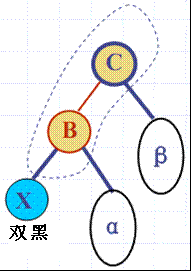
3.“双黑”结点的处理
分三种情况：（1）双黑色结点的兄弟结点是黑色，且子结点有红色结点
（2）双黑结点的兄弟结点是黑色，且有两个黑色结点
（3）双黑结点的兄弟结点是红色结点
(1)双黑结点的兄弟结点是黑色，且子结点有红色结点
A种情况：双黑结点远侄子结点（双黑结点若为左孩子，则双黑结点的兄弟结点的右孩子为远侄子结点；同理，处理双黑结点为右孩子）为红色，如图2
处理方法： 把兄弟结点染为双黑结点的父亲结点的颜色，把兄弟结点的右孩子染为黑色，再把父结点染为黑色；然后针对父结点进行一次左旋转，如科3。
图2 图3
B种情况： 双黑结点近侄子结点（双黑结点若为左孩子，则双黑结点的兄弟结点的左孩子为近侄子结点；同理，处理双黑结点为右孩子）为红，如图4
处理方法： 针对双黑结点的兄弟做一次右旋转，结果使双黑结点的近侄子成为双黑结点新的兄弟；将新兄弟结点着为双黑结点的父结点的颜色，父结点着为黑色，再针对父做一次左旋转，如图5
图5
（2）双黑结点的兄弟结点是黑色，且有两个黑色结点，如图6
处理方法： 把双黑结点的兄弟结点着为红色，双黑结点的父结点着为黑色；若父结点原来为红色，则算法结束；若父结点原来黑色，则将父结点作为双黑结点，继续调整， 直到双黑节点等于根节点时停止。 如图7
图6 图7
（3）双黑结点的兄弟结点是红色结点，如图8
处理方法：进行一次旋转，转换为情况1或情况2，并改变双黑结点的兄弟结点的颜色及父结点的颜色 ， 如图9
图8 图9
三、例子
有一棵红黑树12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17，如图10
图10
1.删除结点12
结点12有两个非空子结点，首先调整为叶结点，与其后继结点13进行 值交换， 然后删除12；由于后继结点为黑色，删除后出现“双黑”，
如图11
图11
此时，属于第一种情况的A种，处理后结果如图12
图12
2.删除1结点
1结点有两个非空子结点，调整为叶子结点，与其后继结点2进行值 交换；此时，1结点只有一个非空子结点，则删除1结点后，将其子结点着为黑色，处理结果如图13
图13
3.删除9
9结点为根结点，调整为叶结点，与后继结点10值交换，由于后继结点为黑色，删除后9后，出现双黑，如图14
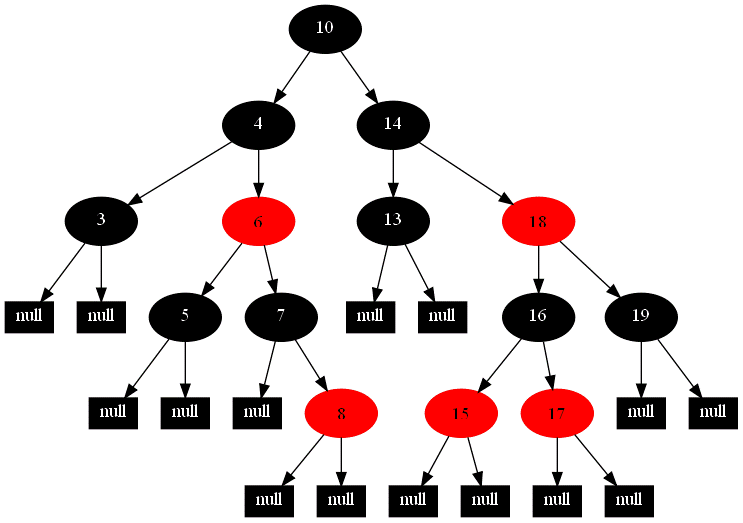
图14
此时为双黑处理第二种情况，处理后，如图15
图15
4.删除结点2
结点2有两个非空子结点，与后继结点3值交换；后继结点为黑色，删除2后，出现双黑；如图16
图16
此时，为双黑处理第二种情况，处理后，如图17
图17
5.删除结点0
结点0为红色结点，直接删除即可
6.删除结点11
结点11有一个非空子结点，为第二种情况，删除11 后，将其非空子结点着为黑色，如图18
图18
7.删除结点7
结点7有一个非空子结点，也为第二种情况，删除7后，将其非空子结点着为黑色；
8.删除结点19
结点19为叶子结点，且为黑色，删除后出现“双黑”，属于双黑处理的第一种情况，处理后如图19
图19
9.删除结点4
结点4有两个非空子树，与其后继结点5交换；后继结点为黑色，删除4后，出现双黑，此时为双黑处理第二种情况，处理后如图20 
图20
10.删除结点15
结点15为叶子结点，删除后出现“双黑”，此时属于双黑处理第一种情况的B种，处理后如图21
图21
11.删除结点18
结点18为叶子结点，且为黑色，删除后出现双黑，属于双黑处理的第二种情况，处理后，如图22
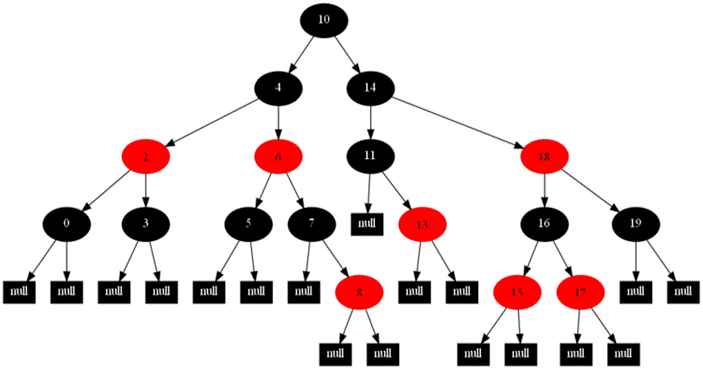
图22
12.删除结点5
结点5有两个子结点，与其后继结点6交换；交换后，结点5只有一个非空子结点，属于第二种情况，直接删除，将非空子结点着黑色，如图23
图23
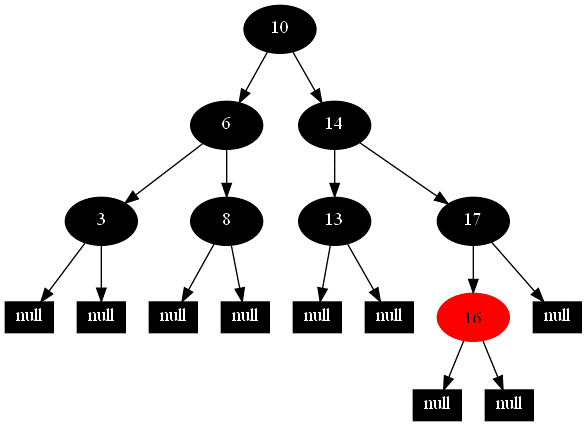
13.删除结点14
结点14有两个子树，与其后继结点16交换；后继结点为红色，交换后14 为红色，直接删除。
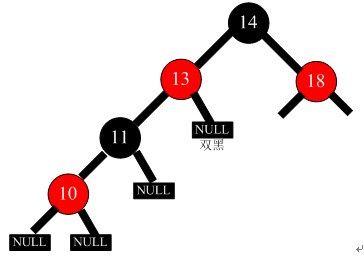
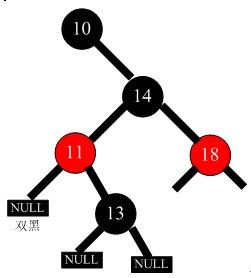
14.删除结点13
结点13为叶子结点，且为黑色，删除后出现“双黑”，属于双黑处理的第二种情况，处理后如图24
图24
15.删除结点10
结点10为根结点，与其后继16值交换；交换后10只有一个非空子结点，直接将10删除，将非空子结点着为黑色
16.删除结点16
结点16为根结点，与后继结点17值交换；交换后16为叶子结点，且为黑色，删除后出现双黑，属于双黑处理的第三种情况，处理后如图25
图25
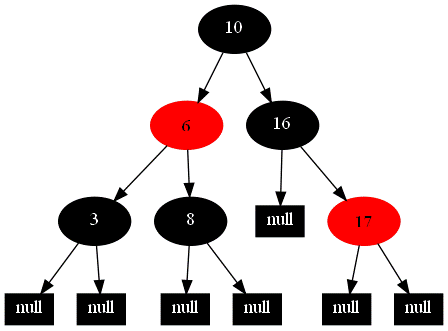
17.删除结点6
结点6为根结点，与后继结点8值交换；交换后，结点6为红色，直接删除
18.删除结点3
结点3为叶子结点，且为黑色，删除后出现“双黑”，属于双黑处理的第二种情况
剩余8：
删除17：
源代码如下：
RedBlackTree.h:
#ifndef _RB_TREE_H_
#define _RB_TREE_H_
#include
#include
#include
#include
using namespace std;
enum NodeColor
{
RED,
BLACK
};
template
class RB_Node //结点类
{
public:
RB_Node() //节点类构造
{
right = NULL;
left = NULL;
parent = NULL;
}
NodeColor RB_COLOR; //颜色
RB_Node* right; //右子树
RB_Node* left; //左子树
RB_Node* parent; //父结点
KEY key; //键
VALUE val; //值
};
template
class RB_Tree
{
//RB树类
private:
RB_Tree(const RB_Tree & input){}
const RB_Tree& operator=(const RB_Tree& input){}
void InOrderTraverse(RB_Node* node); //中序遍历
void clear(RB_Node* node); //清除RB树
//成员变量
RB_Node* m_nullNode;
RB_Node* m_root;
RB_Node* m_DBNode;
public:
RB_Tree(); //构造函数
bool Empty(); //是否为空树
RB_Node* find(KEY key); //查找键key的值
bool Insert(KEY key, VALUE val); //插入
void InsertFixUp(RB_Node* node); //插入后修复
bool RotateLeft(RB_Node* node); //左旋
bool RotateRight(RB_Node* node); //右旋
bool Delete(KEY key); //删除
void DoubleBlackFixUp(RB_Node* node); //双黑修复
RB_Node* FindMin(RB_Node* node);
void InOrderTraverse() //中序遍历外部接口
{
InOrderTraverse(m_root);
}
~RB_Tree()
{
clear(m_root);
delete m_nullNode;
}
};
template
RB_Tree::RB_Tree() //构造函数
{
this->m_nullNode = new RB_Node();
this->m_root = m_nullNode;
this->m_nullNode->right = this->m_root;
this->m_nullNode->left = this->m_root;
this->m_nullNode->parent = this->m_root;
this->m_nullNode->RB_COLOR = BLACK;
this->m_DBNode= new RB_Node();
this->m_DBNode->RB_COLOR = BLACK;
this->m_DBNode->left = m_nullNode;
this->m_DBNode->right = m_nullNode;
};
template
bool RB_Tree::Empty()
{
if(this->m_root==this->m_nullNode)
{
return true;
}
else
{
return false;
}
}
template
RB_Node* RB_Tree::find(KEY key) //查找，此处可递归，参考上一篇二叉查找树
{
RB_Node* index = m_root;
while(index!=m_nullNode)
{
if(keykey)
{
index = index->left;
}
else if(key>index->key)
{
index = index->right;
}
else
{
break;
}
}
return index;
}
/*
左旋，构造一个指针lower_right指向旋转点的右孩子。
lower_right的父结点为旋转点的父结点,旋转点的右孩子为lower_right的左孩子（如果左孩子不为空，则还要设置左孩子的父亲为旋转点）。
判断旋转点是否为根节点。是的话更改m_root的值，否则更改旋转点的父结点左孩子 or 右孩子的指向。
更改旋转点父结点为lower_right，lower_right的左孩子为旋转点
*/
template
bool RB_Tree::RotateLeft(RB_Node* node)
{
if(node==m_nullNode || node->right==m_nullNode)
{
return false; //不能旋转
}
RB_Node* lower_right = node->right;
lower_right->parent = node->parent;
node->right = lower_right->left;
if(lower_right->left!=m_nullNode)
{
lower_right->left->parent = node;
}
if(node->parent==m_nullNode)
{
m_root = lower_right;
m_nullNode->right = m_root;
m_nullNode->left = m_root;
}
else
{
if (node == node->parent->left)
{
node->parent->left = lower_right;
}
else
{
node->parent->right = lower_right;
}
}
node->parent = lower_right;
lower_right->left = node;
}
template
bool RB_Tree::RotateRight(RB_Node* node) //右旋，原理同左旋,left和right交换就可以
{
if (node == m_nullNode || node->left == m_nullNode)
{
return false;//can't rotate
}
RB_Node* lower_left = node->left;
node->left = lower_left->right;
lower_left->parent = node->parent;
if (lower_left->right != m_nullNode)
{
lower_left->right->parent = node;
}
if (node->parent == m_nullNode) //node is root
{
m_root = lower_left;
m_nullNode->left = m_root;
m_nullNode->right = m_root;
//m_nullNode->parent = m_root;
}
else
{
if (node == node->parent->right)
{
node->parent->right = lower_left;
}
else
{
node->parent->left = lower_left;
}
}
node->parent = lower_left;
lower_left->right = node;
}
/*
插入，while循环将insert_point指向要插入的点
如果插入点已经存在，返回false，如果插入的是一颗空树，直接赋值给根节点。否则在插入点赋值
*/
template
bool RB_Tree::Insert(KEY key, VALUE val)
{
RB_Node* insert_point = m_nullNode;
RB_Node* index = m_root;
while(index!=m_nullNode)
{
insert_point = index;
if(keykey)
{
index = index->left;
}
else if (key > index->key)
{
index = index->right;
}
else
{
return false;
}
} //此时insert_point指向要插入的点
RB_Node* insert_node = new RB_Node(); //构造插入的结点
insert_node->key = key;
insert_node->val = val;
insert_node->RB_COLOR = RED;
insert_node->right = m_nullNode;
insert_node->left = m_nullNode;
if(insert_point==m_nullNode) //如果是一颗空树
{
m_root = insert_node;
m_root->parent = m_nullNode;
m_nullNode->left = m_root;
m_nullNode->right = m_root;
m_nullNode->parent = m_root;
}
else
{
if(key < insert_point->key)
{
insert_point->left = insert_node;
}
else
{
insert_point->right = insert_node;
}
insert_node->parent = insert_point;
}
InsertFixUp(insert_node); //调用InsertFixUp修复红黑树性质
}
/*
A 父亲节点为红色时才修复
插入修复：分为插入点的父结点是祖父结点的左孩子还是右孩子
B 左孩子的话：
C 创建一个uncle结点指向叔叔节点（父结点的兄弟）。
D 1）如果叔叔结点为红色：父结点和叔叔结点变黑，祖父节点变红且作为当前结点
E 2）叔叔节点为黑色：如果插入节点是父节点的右孩子：父结点作为当前节点然后左旋，转换为情况三继续处理
F 3）叔叔节点为黑色：插入节点为左孩子：父结点变黑，祖父变红，祖父结点为支点右旋
G 右孩子的话：
*/
template
void RB_Tree::InsertFixUp(RB_Node* node)
{
while(node->parent->RB_COLOR==RED) //A
{
if(node->parent==node->parent->parent->left) //B
{
RB_Node* uncle = node->parent->parent->right; //C
if(uncle->RB_COLOR==RED) //D
{
node->parent->RB_COLOR = BLACK;
uncle->RB_COLOR = BLACK;
node->parent->parent->RB_COLOR = RED;
node = node->parent->parent;
}
else if(uncle->RB_COLOR==BLACK)
{
if(node==node->parent->right) //E
{
node = node->parent;
RotateLeft(node);
}
//F
node->parent->RB_COLOR = BLACK;
node->parent->parent->RB_COLOR = RED;
RotateRight(node->parent->parent);
}
}
else //G
{
RB_Node* uncle = node->parent->parent->left;
if (uncle->RB_COLOR == RED)
{
node->parent->RB_COLOR = BLACK;
uncle->RB_COLOR = BLACK;
uncle->parent->RB_COLOR = RED;
node = node->parent->parent;
}
else if (uncle->RB_COLOR == BLACK)
{
if (node == node->parent->left)
{
node = node->parent;
RotateRight(node);
}
node->parent->RB_COLOR = BLACK;
node->parent->parent->RB_COLOR = RED;
RotateLeft(node->parent->parent);
}
}
}
m_root->RB_COLOR = BLACK; //修复根节点颜色，防止被改为红色
}
/*
删除一个结点：
*/
template
bool RB_Tree::Delete(KEY key)
{
RB_Node* delete_point = find(key); //找到要删除的点
if(delete_point==m_nullNode)
{
return false;
}
if(delete_point->left!=m_nullNode && delete_point->right!=m_nullNode) //有两个子结点
{
RB_Node* replace_node = FindMin(delete_point->right);
//删除点和替换点的值互换，结点颜色不换
KEY tmpkey=delete_point->key;
VALUE tmpval=delete_point->val;
delete_point->key = replace_node->key;
delete_point->val = replace_node->val;
replace_node->key = tmpkey;
replace_node->val = tmpval;
delete_point = replace_node;
}
RB_Node* delete_point_child;
if(delete_point->RB_COLOR==RED) //若该节点为红色
{
if (delete_point == delete_point->parent->left) //如果是左孩子
{
delete_point->parent->left = m_nullNode;
}
else //如果是右孩子
{
delete_point->parent->right = m_nullNode;
}
delete delete_point;
}
else if(delete_point->right!=m_nullNode) //如果右结点不为空,此时要删除的结点肯定为黑色，且右结点肯定为红色
{
if(delete_point==delete_point->parent->left) //要删除的点是左结点
{
delete_point->parent->left = delete_point->right;
delete_point->right->parent = delete_point->parent;
}
else
{
delete_point->parent->right = delete_point->right;
delete_point->right->parent = delete_point->parent;
}
delete_point->right->RB_COLOR = BLACK; //右结点颜色改为黑色
delete delete_point;
}
else if(delete_point->left!=m_nullNode) //如果左结点不为空（未经过替换），与右节点不为空操作一样
{
if (delete_point == delete_point->parent->left) //要删除的点是左结点
{
delete_point->parent->left = delete_point->left;
delete_point->left->parent = delete_point->parent;
}
else
{
delete_point->parent->right = delete_point->left;
delete_point->left->parent = delete_point->parent;
}
delete_point->left->RB_COLOR = BLACK; //右结点颜色改为黑色
delete delete_point;
}
else //无子节点的情况
{
//此时唯一剩下情况为，要删除结点为黑色且无子结点
if (delete_point->parent == m_nullNode) //如果要删除的是根节点
{
m_root = m_nullNode;
m_nullNode->parent = m_root;
m_nullNode->left = m_root;
m_nullNode->left = m_root;
delete delete_point;
}
else
{
RB_Node* tmp = delete_point->parent;
if (delete_point == delete_point->parent->left) //如果要删除结点为左节点
{
delete delete_point;
tmp->left = m_DBNode;
m_DBNode->parent = tmp;
DoubleBlackFixUp(m_DBNode);
tmp->left = m_nullNode;
}
else //如果要删除结点为右节点
{
delete delete_point;
tmp->right = m_DBNode;
m_DBNode->parent = tmp;
DoubleBlackFixUp(m_DBNode);
tmp->right = m_nullNode;
}
}
}
}
/*
双黑修复
*/
template
void RB_Tree::DoubleBlackFixUp(RB_Node* node) //传过来的参数都是双黑结点
{
if(node==node->parent->left) //如果此结点是左结点
{
RB_Node* brother = node->parent->right;
//情况3
if (brother->RB_COLOR == RED)
{
node->parent->RB_COLOR = RED;
brother->RB_COLOR = BLACK;
RotateLeft(node->parent);
//之后转入情况1或2
}
//情况1
if(brother->RB_COLOR==BLACK && (brother->left->RB_COLOR==RED || brother->right->RB_COLOR==RED))
{
if(brother->right->RB_COLOR==RED) //A
{
brother->RB_COLOR = node->parent->RB_COLOR;
brother->right->RB_COLOR == BLACK;
node->parent->RB_COLOR = BLACK;
RotateLeft(node->parent);
}
else //B
{
RotateRight(brother);
node->parent->right->RB_COLOR = node->parent->RB_COLOR;
node->parent->RB_COLOR = BLACK;
RotateLeft(node->parent);
}
}
//情况2
else if(brother->RB_COLOR==BLACK && (brother->left->RB_COLOR == BLACK && brother->right->RB_COLOR == BLACK))
{
while(node->parent!=m_nullNode) //当node不是根节点的时候
{
brother->RB_COLOR = RED;
if(node->parent->RB_COLOR==RED) //父结点原来为红色
{
node->parent->RB_COLOR = BLACK;
break;
}
else //父结点本来就是黑色
{
node = node->parent;
}
}
}
}
else //如果此节点是右结点，把左结点情况 left和right调换就可以
{
RB_Node* brother = node->parent->left;
//情况3
if (brother->RB_COLOR == RED)
{
node->parent->RB_COLOR = RED;
brother->RB_COLOR = BLACK;
RotateRight(node->parent);
//之后转入情况1或2
}
//情况1
if (brother->RB_COLOR == BLACK && (brother->right->RB_COLOR == RED || brother->left->RB_COLOR == RED))
{
if (brother->left->RB_COLOR == RED) //A,远侄子
{
brother->RB_COLOR = node->parent->RB_COLOR;
brother->left->RB_COLOR = BLACK;
node->parent->RB_COLOR = BLACK;
RotateRight(node->parent);
}
else //B
{
RotateLeft(brother);
node->parent->left->RB_COLOR = node->parent->RB_COLOR;
node->parent->RB_COLOR = BLACK;
RotateRight(node->parent);
}
}
//情况2
else if (brother->RB_COLOR == BLACK && (brother->right->RB_COLOR == BLACK && brother->left->RB_COLOR == BLACK))
{
while (node->parent != m_nullNode) //当node不是根节点的时候
{
brother->RB_COLOR = RED;
if (node->parent->RB_COLOR == RED) //父结点原来为红色
{
node->parent->RB_COLOR = BLACK;
break;
}
else //父结点本来就是黑色
{
node = node->parent;
}
}
}
}
}
template
RB_Node* RB_Tree::FindMin(RB_Node* node)
{
if (node->left == m_nullNode)
return node;
return FindMin(node->left);
}
template //中序遍历
void RB_Tree::InOrderTraverse(RB_Node* node)
{
if (node == m_nullNode)
{
return;
}
else
{
InOrderTraverse(node->left);
cout << node->key << endl;
InOrderTraverse(node->right);
}
}
template
void RB_Tree::clear(RB_Node* node)
{
if (node == m_nullNode)
{
return;
}
else
{
clear(node->left);
clear(node->right);
delete node;
}
};
#endif
RedBlackTree.cpp
#include
#include
#include
#include
#include
#include"RedBlackTree.h"
using namespace std;
int main()
{
RB_Tree tree;
vector v;
for (int i = 0; i < 20; ++i)
{
v.push_back(i);
}
random_shuffle(v.begin(), v.end());
copy(v.begin(), v.end(), ostream_iterator(cout, " "));
cout << endl;
stringstream sstr;
for (int i = 0; i < v.size(); ++i)
{
tree.Insert(v[i], i);
cout << "insert:" << v[i] << endl; //添加结点
}
tree.InOrderTraverse();
for (int i = 0; i < v.size(); ++i)
{
cout << "Delete:" << v[i] << endl;
tree.Delete(v[i]); //删除结点
tree.InOrderTraverse();
}
cout << endl;
tree.InOrderTraverse();
return 0;
} 结果如下图：
