解题--＞在线OJ(八)
解题-->栈、队列、二叉树
- 1.最小栈
- 2.设计循环队列
- 3.二叉树的前序遍历
-
- 4.二叉树的中序遍历
- 5.二叉树的后序遍历
- 6.相同的树
-
- 7.另一棵树的子树
- 8.二叉树的最大深度
- 9.平衡二叉树
- 10.对称二叉树
1.最小栈
链接: https://leetcode-cn.com/problems/min-stack/.
解题思路：
push:将元素入栈;
pop:获取栈顶元素并且栈顶元素出栈;
top:获取栈顶元素，但是，栈顶元素不出栈；
getMin:获取栈中的最小元素；
创建两个栈，一个是元素正常入栈dataStack，一个是记录栈中的最小元素minStack；
在入栈的时候，如果minStack为空，就直接将元素入栈，如果不为空，将元素与minStack的栈顶元素相比较，如果小于栈顶元素，入栈，否则，不入栈；
在出栈的时候，记录下dataStack的出栈的数字，然后与minStack的栈顶元素相比较，如果一致，就出栈；
获取栈顶元素，直接返回dataStack的栈顶元素；
获取栈中的最小元素，直接返回minStack的栈顶元素。
class MinStack {
Stack<Integer> dataStack;
Stack<Integer> minStack;
public MinStack() {
dataStack=new Stack<>();
minStack=new Stack<>();
}
public void push(int val) {
dataStack.push(val);
if(minStack.isEmpty() || val<=minStack.peek()){
minStack.push(val);
}
}
public void pop() {
int temp=dataStack.pop();
if(temp==minStack.peek()){
minStack.pop();
}
}
public int top() {
return dataStack.peek();
}
public int getMin() {
return minStack.peek();
}
}
2.设计循环队列
链接: https://leetcode-cn.com/problems/design-circular-queue/.
解题思路：
用数组来实现循环队列
class MyCircularQueue {
int[] arr=null;
int capacity=0; //记录容量
int front=0; //对头指针
int rear=0; //队尾指针
int size=0; //记录当前队列中已经存入元素的个数
public MyCircularQueue(int k) {
arr=new int[k];
this.capacity=k;
}
public boolean enQueue(int value) {
//如果队满的话，直接返回false
if(capacity==size){
return false;
}
//如果队不满的话，直接将value进队
arr[rear]=value;
rear=(rear+1)%capacity;
size++;
return true;
}
public boolean deQueue() {
//如果队列为空，直接返回false
if(size==0){
return false;
}
//队不为空的时候，将对头元素出队
front=(front+1)%capacity;
size--;
return true;
}
//返回对头元素
public int Front() {
//如果队列为空，返回-1
if(size==0){
return -1;
}
return arr[front];
}
//返回队尾元素
public int Rear() {
if(size==0){
return -1;
}
return arr[(rear-1+capacity)%capacity];
}
//判断循环队列是否为空
public boolean isEmpty() {
return size==0;
}
//判断循环队列是否已满
public boolean isFull() {
return size==capacity;
}
}
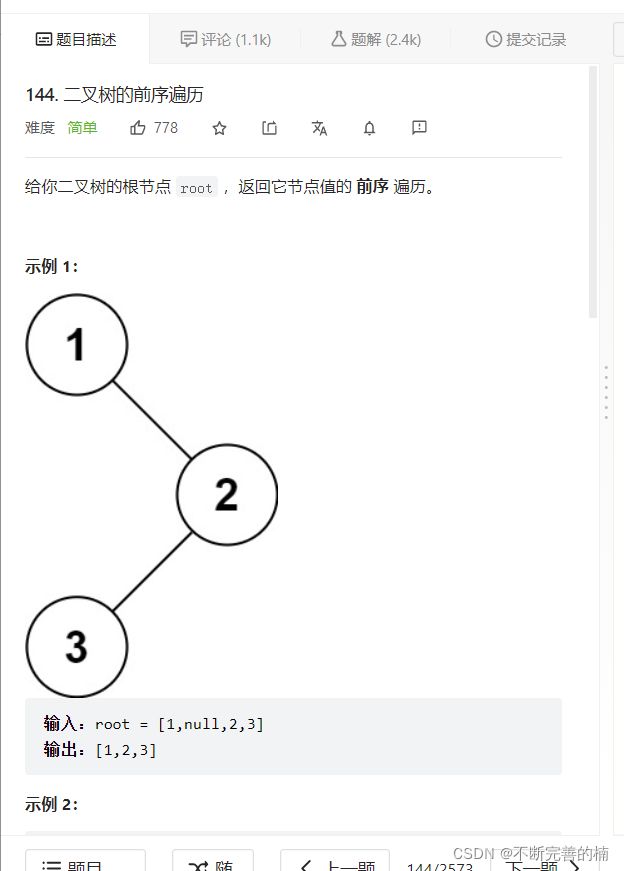
3.二叉树的前序遍历
链接: https://leetcode-cn.com/problems/binary-tree-preorder-traversal/.
针对二叉树的前序遍历有两种方案，一种是递归，一种是栈
前序遍历是：根左右
递归：因为这个题目需要返回一个list列表，所以，创建一个list列表，将根节点的值先入列表，然后递归根节点的左子树，左子树遍历完之后，再递归遍历右子树。
栈：先将根节点入栈，循环，条件是：栈不为空
将根节点出栈，并且将根节点对应的值放在对应的list列表当中，因为前序遍历是：根左右，栈的特点是：先进后出，所以，先让根节点的右子树入栈，再将左子树入栈，然后再拿到左子节点，再判断左子节点的右子树和左子树是否为空，不为空，就入栈。
进入栈的顺序是：根—>右—>左
根在右入栈的时候，就出栈了，并且将值加入了list了。
//1.运用递归的方式来解决此问题
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list=new ArrayList<>();
if(root==null){
return list;
}
list.add(root.val);
list.addAll(preorderTraversal(root.left));
list.addAll(preorderTraversal(root.right));
return list;
}
}
//2.用栈的方式解决此问题
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list=new ArrayList<>();
Stack<TreeNode> stack=new Stack<>();
if(root==null){
return list;
}
stack.push(root);
while(!stack.isEmpty()){
TreeNode node=stack.pop();
list.add(node.val);
if(node.right!=null){
stack.push(node.right);
}
if(node.left!=null){
stack.push(node.left);
}
}
return list;
}
}
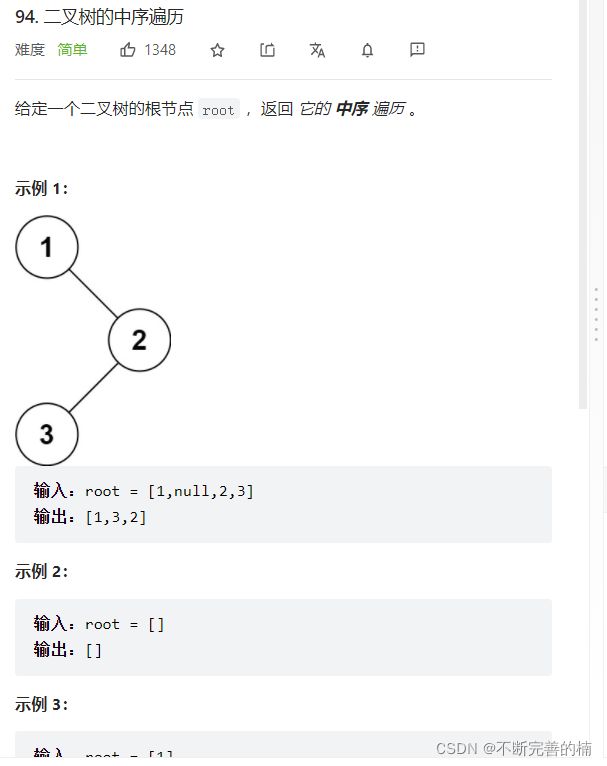
4.二叉树的中序遍历
链接: https://leetcode-cn.com/problems/binary-tree-inorder-traversal/.
//1.用递归的方式解决此问题
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list=new ArrayList<>();
if(root==null){
return list;
}
list.addAll(inorderTraversal(root.left));
list.add(root.val);
list.addAll(inorderTraversal(root.right));
return list;
}
}
//2.用栈的方式解决此问题
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list=new ArrayList<>();
Stack<TreeNode> stack=new Stack<>();
if(root==null){
return list;
}
stack.push(root);
while(!stack.isEmpty()){
TreeNode node=stack.peek();
while(node.left!=null){
stack.push(node.left);
node=node.left;
}
while(!stack.isEmpty()){
TreeNode temp=stack.pop();
list.add(temp.val);
if(temp.right!=null){
stack.push(temp.right);
break;
}
}
}
return list;
}
}
5.二叉树的后序遍历
链接: https://leetcode-cn.com/problems/binary-tree-postorder-traversal/.
//1.用递归的方式解决
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list=new ArrayList<>();
if(root==null){
return list;
}
list.addAll(postorderTraversal(root.left));
list.addAll(postorderTraversal(root.right));
list.add(root.val);
return list;
}
}
//2.用栈的方式解决
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list=new ArrayList<>();
Stack<TreeNode> stack=new Stack<>();
if(root==null){
return list;
}
stack.push(root);
TreeNode lastNode=null;
while (!stack.isEmpty()){
while(stack.peek().left!=null){
stack.push(stack.peek().left);
}
while(!stack.isEmpty()){
if(lastNode == stack.peek().right ||stack.peek().right==null){
TreeNode temp=stack.pop();
list.add(temp.val);
lastNode = temp;
}else if(stack.peek().right!=null){
stack.push(stack.peek().right);
break;
}
}
}
return list;
}
}
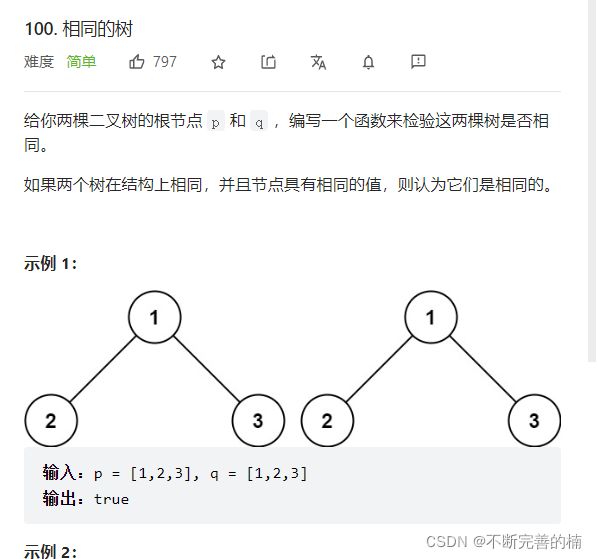
6.相同的树
链接: https://leetcode-cn.com/problems/same-tree/.
解题思路：
首先判断这两个节点是否都为空，都为空，返回true;
如果两个节点其中之一为空的话，直接返回false;
如果两个节点都不为空的话，就判断两个节点的值是否相同，不相同直接返回false,相同的话，就直接在进一步的判断，看两个节点的左子节点是否相等和右子节点是否相等。
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p==null && q==null){
return true;
}else if(p==null||q==null){
return false;
}else if(p.val !=q.val){
return false;
}else{
return isSameTree(p.left,q.left)&&isSameTree(p.right,q.right);
}
}
}
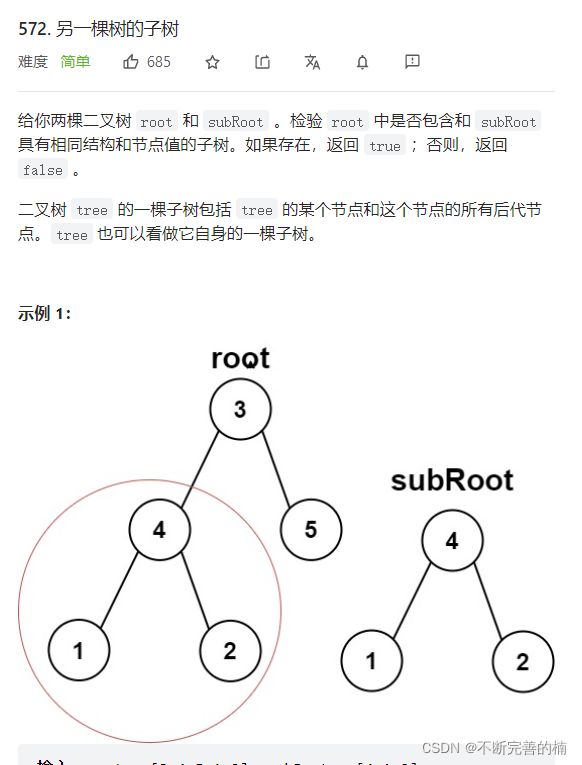
7.另一棵树的子树
链接: https://leetcode-cn.com/problems/subtree-of-another-tree/.
解题思路：
创建了一个isSameTree方法，目的是判断两个树是否相同；
递归isSubtree这个方法，目的是找到root树下的某个等于subRoot根节点的节点，找到后，判断两个节点下的树是否相同，如果将root遍历到null，就直接返回false即可。
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
if(root==null){
return false;
}
return isSameTree(root,subRoot)||
isSubtree(root.left,subRoot)||
isSubtree(root.right,subRoot);
}
public static boolean isSameTree(TreeNode root,TreeNode subRoot){
if(root==null && subRoot==null){
return true;
}else if(root==null || subRoot==null){
return false;
}else if(root.val != subRoot.val){
return false;
}else{
return isSameTree(root.left,subRoot.left)&&isSameTree(root.right,subRoot.right);
}
}
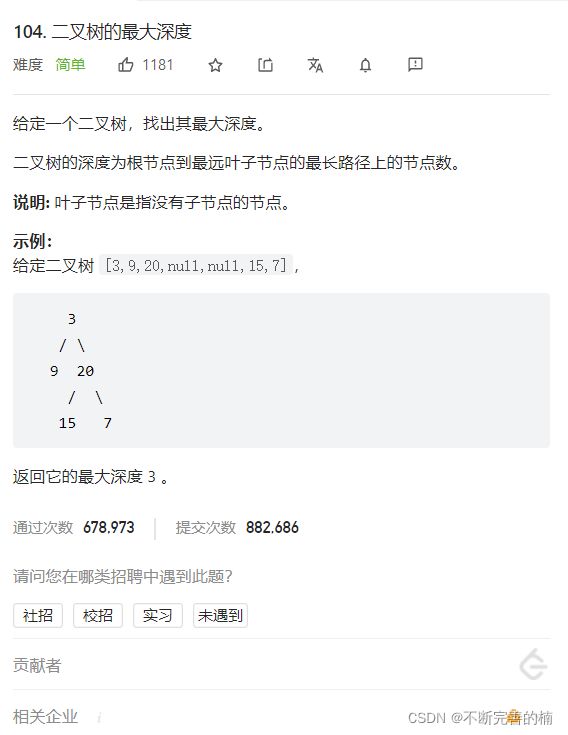
8.二叉树的最大深度
链接: https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/.
解题思路：
如果root等于null，就直接返回0
否则，就递归root的左子树和右子树，最终树的最大深度，就是1+(root左子树，root右子树)最大深度
class Solution {
public int maxDepth(TreeNode root) {
if(root==null){
return 0;
}
return 1+Math.max(maxDepth(root.left),maxDepth(root.right));
}
}
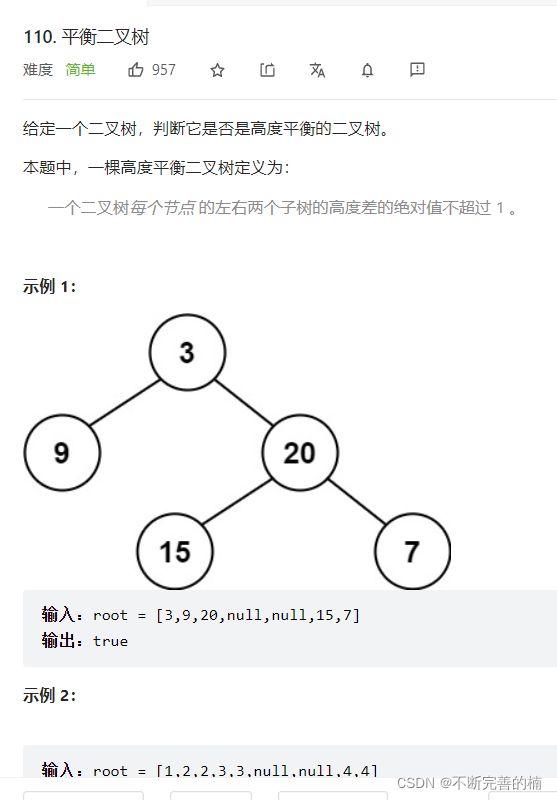
9.平衡二叉树
解题思路：
递归每个节点，计算出每个节点的左右子树的最大深度，判断左右子树的最大深度差是否大于等于1，如果大于1，该树就不是平衡二叉树。如果该树上每个节点的左右子树的最大深度差都小于等于1，那就证明这个树是平衡二叉树。
class Solution {
public boolean isBalanced(TreeNode root) {
if(root==null){
return true;
}
return Math.abs(maxDepth(root.left)-maxDepth(root.right))<=1 &&
isBalanced(root.left) &&
isBalanced(root.right);
}
public static int maxDepth(TreeNode root){
if(root==null){
return 0;
}
return 1+Math.max(maxDepth(root.left),maxDepth(root.right));
}
}
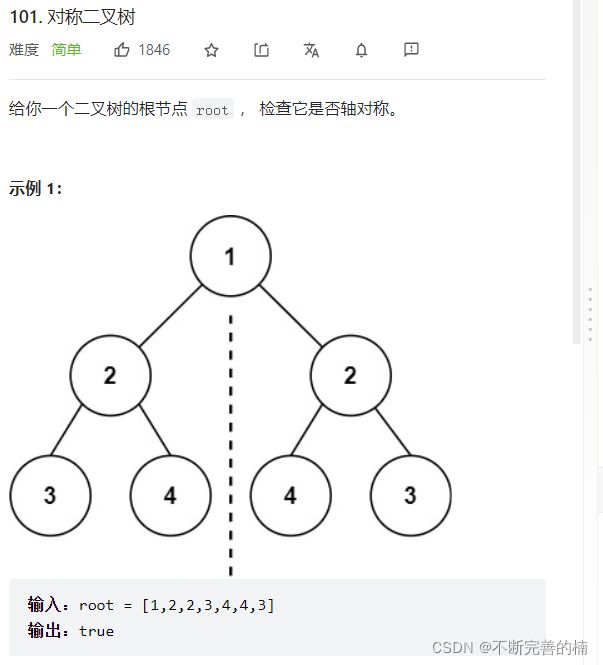
10.对称二叉树
链接: https://leetcode-cn.com/problems/symmetric-tree/.
class Solution {
public boolean isSymmetric(TreeNode root) {
return judge(root,root);
}
public static boolean judge(TreeNode m,TreeNode n){
if(m==null && n==null){
return true;
}else if(m==null || n==null){
return false;
}else if(m.val!=n.val){
return false;
}else{
return judge(m.left,n.right)&& judge(m.right,n.left);
}
}
}