再见“黑匣子模型“！SHAP 可解释 AI (XAI)实用指南来了！

我们知道模型可解释性已成为机器学习管道的基本部分，它使得机器学习模型不再是"黑匣子"。幸运的是，近年来机器学习相关工具正在迅速发展并变得越来越流行。本文主要是针对回归问题的 SHAP 开源 Python 包进行 XAI 分析。

Lundberg 和 Lee (2016) 的 SHAP（Shapley Additive Explanations）是一种基于游戏理论上最优的 Shapley value来解释个体预测的方法。 Shapley value是合作博弈论中一种广泛使用的方法，它具有令人满意的特性。从博弈论的角度，把数据集中的每一个特征变量当成一个玩家，用该数据集去训练模型得到预测的结果，可以看成众多玩家合作完成一个项目的收益。Shapley value，通过考虑各个玩家做出的贡献，来公平的分配合作的收益。

在本文中，我们将使用来自 sklearn 数据集的波士顿房价数据集进行示例展示，它是一个简单的回归问题。

boston = datasets.load_boston() 
X_train, X_test, y_train, y_test = model_selection.train_test_split(boston.data, boston.target, random_state=0)

拆分数据集进行训练和测试后，创建模型并拟合。

regressor = ensemble.RandomForestRegressor() 
regressor.fit(X_train, y_train);

计算Shapley value

使用 SHAP 包，计算非常简单明了。我们只需要模型（regressor）和数据集（X_train）。

# Create object that can calculate shap values
explainer = shap.TreeExplainer(regressor)
# Calculate Shap values
shap_values = explainer.shap_values(X_train)

计算 SHAP 值后，我们可以绘制几个分析图，以帮助我们理解模型。

SHAP 特征重要性

SHAP 提供了特征重要性的计算方式，取每个特征的SHAP value的绝对值的平均值作为该特征的重要性，得到一个标准的条形图。在下图中，你可以看到由 SHAP value计算的特征重要性与使用 scikit-learn 计算的特征重要性之间的比较，它们看起来非常相似，但它们并不相同。

shap.summary_plot(shap_values, X_train, feature_names=features, plot_type="bar")

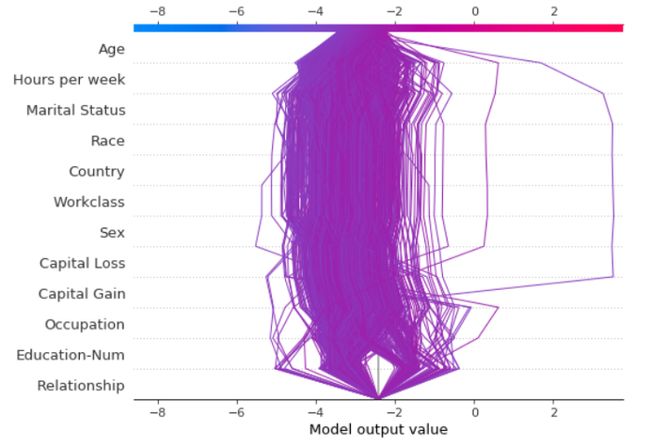
SHAP Summary Plot

Summary_plot 结合了特征重要性和特征效果。Summary_plot 为每一个样本绘制其每个特征的Shapley value。y 轴上的位置由特征确定，x 轴上的位置由每 Shapley value 确定。颜色表示特征值（红色高，蓝色低），可以看到特征 LSTAT 是最重要的特征，具有很高的 Shapley value范围。重叠点在 y 轴方向抖动，因此我们可以了解每个特征的 Shapley value分布,这些特征是根据它们的重要性排序的。

shap.summary_plot(shap_values, X_train, feature_names=features)

在Summary_plot图中，我们首先看到了特征值与对预测的影响之间关系的迹象,但是要查看这种关系的确切形式，我们必须查看 SHAP Dependence Plot图。

SHAP Dependence Plot

Partial dependence plot (PDP or PD plot) 显示了一个或两个特征对机器学习模型的预测结果的边际效应,它可以显示目标和特征之间的关系是线性的、单调的还是更复杂的。PDP是一种全局方法：该方法考虑所有实例并给出关于特征与预测结果的全局关系。PDP 的一个假设是第一个特征与第二个特征不相关。如果违反此假设，则PDP计算的平均值将包括极不可能甚至不可能的数据点。

Dependence plot 是一个散点图，显示单个特征对模型预测的影响。在这个例子中，当每个住宅的平均房间数高于 6 时，房产价值会显着增加。

• 每个点都是来自数据集的单个预测（行）。
• x 轴是数据集中的实际值。
• y 轴是该特征的 SHAP 值，它表示该特征值对该预测的模型输出的改变程度。

颜色对应于可能与我们正在绘制的特征有交互作用的第二个特征（默认情况下，第二个特征是自动选择的）。如果另一个特征与我们正在绘制的特征之间存在交互作用，它将显示为不同的垂直着色模式。

shap.dependence_plot(5, shap_values, X_train, feature_names=features)

在上面的例子中，我们可以看到每个住宅的平均房间数高于 7.5，CRIM 总是很低。这些案例的 Shapley value很高，极大地影响了结果,可以看出 RM、CRIM 特征之间相互作用。

SHAP Force plot

SHAP force plot为我们提供了单一模型预测的可解释性，可用于误差分析，找到对特定实例预测的解释。

i = 18 
shap.force_plot(explainer.expected_value, shap_values[i], X_test[i], feature_names = features)

从图中我们可以看出：

• 模型输出值：16.83
• 基值：如果我们不知道当前实例的任何特性，这个值是可以预测的。基础值是模型输出与训练数据的平均值。（代码中的explainer.expected_value）。
• 绘图箭头上的数字是此实例的特征值。CRIM：城镇人均犯罪率 = 0.06664 和 RM：平均房间数 = 6.546
• 红色代表将模型分数推高的特征，蓝色代表将分数推低的特征。
• 箭头越大，特征对输出的影响越大。在 x 轴上可以看到影响的减少或增加量。
• 0.066 的 CRIM 增加属性值，6.546 的 RM 降低属性值。

如果我们想要更全面地展现先前的预测，我们可以使用力图的变体。在这里，我们可以看到一组垂直放置（旋转 90°）和并排放置的预测。在下图中，我们可以看到数据集中的前 5 行。

# visualize the first 5 predictions explanations with a dark red dark blue color map.
shap.force_plot(explainer.expected_value, shap_values[0:5,:], X_test[0:5,:], plot_cmap="DrDb", feature_names=features)

SHAP Decision plot

决策图显示的信息与力图基本相同。灰色垂直线是基础值 ，红线表示每个特征是否将输出值移动到高于或低于平均预测的值。

这张图比前一张图更清晰和直观，尤其是要分析的特征比较多的时候。在力图中，当预测变量的数量较多时，信息可能看起来非常紧凑。

shap.decision_plot(explainer.expected_value[0], shap_values[0], feature_names = list(features))

决策图的垂直直线标记了模型的基础值。彩色线是预测。特征值在预测线旁边以供参考。从图的底部开始，预测线显示 SHAP value 如何从基础值累积到图顶部的模型最终分数。决策图是 SHAP value 的文字表示，使其易于解读。

力图和决策图都可以有效地解释上述模型的预测。而且很容易识别出主要影响的大小和方向。

将决策图叠加在一起有助于根据 SHAP value 定位异常值。在上图中，你可以看到一个不同数据集的示例，用于使用SHAP决策图进行异常值检测。

Summary

SHAP 框架已被证明是机器学习模型解释领域的一个重要发展。 SHAP 结合了几种现有方法，创建了一种直观、理论上合理的方法来解释任何模型的预测。 SHAP value 量化了特征对预测影响的大小和方向（正或负）。 我相信使用 SHAP 和其他工具进行 XAI 分析应该是机器学习管道的一个组成部分。

技术交流

欢迎转载、收藏本文，码字不易，有所收获点赞支持一下！

为方便进行学习交流，本号开通了技术交流群，添加方式如下：

直接添加小助手微信号：pythoner666，备注：CSDN+python，或者按照如下方式添加均可！