统计学习方法笔记（李航）———第一章（统计学习方法概论）

一、基本概念

1. 假设空间 （Hypothesis space）

相对“输入空间”、“输出空间”、“特征空间”等向量空间，假设空间的概念比较抽象。首先它是一个“映射”的集合。什么是映射呢？在这里暂且理解为函数吧。输入空间中的一个 n维向量x，通过函数$f(\cdot )$ 得到了输出空间中的m维向量y：

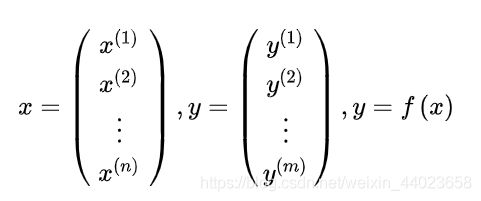
注意：按照符号规定, $x^{(i)}$ 表示此向量的第 $i$ 个分量 (特征) , $x_i$ 表示这是第 $i$ 个向量 (样本)

因此, 假设空间是函数的集合, 即 “函数族" 。记作 $\mathcal{F}=\{f\mid Y=f(X)\}$ 。

2. 模型分类

模型 $\{\begin{array}{l}\text{ 概率模型 }\cdots \cdots \text{ 条件概率分布 }:P(Y\mid X)\\ \text{ 非概率模型 }\cdots \cdots .\text{ 决策函数 }:Y=F(X)\end{array}$

预测结果 $\{\begin{array}{l}\text{ 概率模型 }\cdots \cdots y_{N+1}=\arg {\max }_y\hat{P}\left(y\mid x_{N+1}\right)\\ \text{ 非概率模型 }\cdots \cdots y_{N+1}=\hat{f}\left(x_{N+1}\right)\end{array}$

非概率模型（决策函数）较容易理解，通过对已知数据的 “学习" ，在假设空间中找到合适的 “决 策函数" $\hat{f}$ ，然后通过此模型对 $x_{N+1}$ 进行预测，得到 $y_{N+1}$ 。寻找 $\hat{f}$ 的过程类似于数理 统计中的“点估计" ，需要确定函数 $f_{\theta }(\cdot )$ 的未知参数 $\theta$

概率模型（条件概率分布）则不同, X和Y不能理解为分布函数 $P(Y\mid X)$ 的输入、输出，分布函 数的值域为[0,1]之间的实数, 不能为m维向量。因此X和Y可以看作两个事件，相当于分布函数的 两个参数。

$y_{N+1}=\arg {\max }_y\hat{P}\left(y\mid x_{N+1}\right)$ 该如何理解呢?
argmax表示arguments of maxima，意思是 “最大值的参数”，, 也就是 “求出使得函数出现最大 值的参数” 。它的数学定义如下：

设 $f:X\to Y,\arg {\max }_{x}f(x):=\{x\mid \forall y:f(y)\le f(x)\}$
为了更好地区分argmax 与 max, 下面给出max的定义作为对比：

设 $f:X\to Y,{\max }_{x}f(x):=\{f(x)\mid \forall y:f(y)\le f(x)\}$
可以看到，argmax是自变量（参数）的集合, 可能存在多个值; max是函数值的集合, 最终只有 一个值。

因此 $y_{N+1}=\arg {\max }_y\hat{P}\left(y\mid x_{N+1}\right)$ 可以理解为：对于分布函数 $\hat{P}(Y\mid X),$ 在
$X=x_{N+1}$ 的条件下, $Y=y_{N+1}$ 使得该分布函数取得最大值。

无论是概率模型 $P_{\theta }(Y\mid X)$ 还是非概率模型 $Y=f_{\theta }(X),$ 学习的目的是确定模型的参数 $\theta$ 从而确定决策函数 $f_{\theta }$ 或者条件分布 $P_{\theta }$ 。 $X$ 、 $Y$ 是给定训练数据集，不需要学习。

二、统计学习方法的三要素

统计学习方法都是由“模型、策略和算法”三要素构成，即 方法 = 模型 + 策略 + 算法 。此处主要讨论监督学习的三要素。

1. 模型
   前文已详细地讨论过两种模型，假设空间可以表示为：

   • 非概率模型
     $$\mathcal{F}=\left\{f\mid Y=f_{\theta }(X),\theta \in R^n\right\}$$
   • 概率模型
     $$\mathcal{F}=\left\{P\mid P_{\theta }(Y\mid X),\theta \in R^n\right\}$$
     参数向量 $\theta$ 所在的空间 $R^n$ 称为 “参数空间" 。一般来说，在假设空间中寻找模型, 相当于在 参数空间中寻找一个合适的参数向量。

2. 策略

如何判断一个参数向量是否合适？或者说：如何判断一个模型是最优模型？

在已知数据中，模型的预测值与真实值差距越小，则表示模型越好，对应的参数向量越合适。这一判别标准就是所谓的“策略”。

为此引入：损失函数（loss function）、风险函数（risk function）的概念。

• 损失函数
  度量一次预测的好坏，就是说对于一个样本，它的预测值与真实值的误差。书中介绍了4种损失函数，对于分类问题，常用0-1损失函数：
  $$L(Y,f(X))=\{\begin{array}{l}1,Y\ne f(X)\\ 0,Y=f(X)\end{array}$$
  对于回归问题，最常用的是
  • 平方损失函数 (非概率模型) : $L(Y,f(X))=(Y-f(X){)}^2$
  • 对数损失函数 (概率模型) $:L(Y,P(Y\mid X))=-\log P(Y\mid X)$

平方损失函数的值越小，表示预测值与真实值误差越小，因此模型越好。

但对数损失函数则不能用误差来理解，因为 $P(Y\mid X)$ 表示在X条件下，Y出现的概率，应该是概率越大模型越好。函数 $L=-\log z$ 的图像如下：

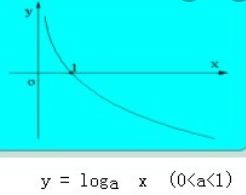
当 $z=P(Y\mid X)\in [0,1]$ 时, 由于 $L=-\log z$ 为减函数, 因此z越接近1（发生概率越 高），则损失函数的值就越接近于0 （损失函数越小）。

• 风险函数
  由于损失函数只度量一次预测的好坏，评判一个模型的好坏需要看长期的发挥，因此用损失函数的 数学期望定义 “风险函数” ，表示模型 $f(x)$ 在总体分布 $P(X,Y)$ 下的平均损失。
  $$R_{exp}(f)=E_P[L(Y,f(X))]={\int }_{\mathcal{X},\mathcal{Y}}L(y,f(x))P(x,y)dxdy$$

• 经验风险(empirical risk)
  实际上，我们并不知道总体分布 $P(X,Y)$ 是什么，否则就不需要学习和预测了，只能通过样本统 计量估计风险函数（L的期望值）。
  $$R_{emp}(f)=\frac{1}{N}\sum _{i=1}^{N}L\left(y_i,f\left(x_i\right)\right)$$
  当N趋于无穷时，经验风险收敛于期望风险（即风险函数）。

• 结构风险（structural risk）
  当样本容量足够大时，经验风险有很好的效果。但当样本容量很小时，容易造成“过拟合”（后面会解释）。为了解决这一问题，在经验风险的基础上增加一个“正则化项”（即惩罚项），得到结构风险。
  $$R_{srm}(f)=\frac{1}{N}\sum _{i=1}^{N}L\left(y_i,f\left(x_i\right)\right)+\lambda J(f)$$
  $J(f)$ 为模型的复杂度, 模型越复杂则结构风险越大。 $\lambda \ge 0$ 用于权衡经验风险与模型复杂 度, 结构风险小需要经验风险和模型复杂度同时小。
  所谓模型复杂度, 可以理解为未知参数的个数。以多项式模型为例，次数越低模型就越简单, 一次 多项式 $f(x)={\theta }_0+{\theta }_{1}x$ 就比二次多项式 $f(x)={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2$ 简单。正如奥卡姆弟
  刀所言：如无必要，勿增实体。

• 两种策略
  经验风险最小化： ${\min }_{f\in \mathcal{F}}\frac{1}{N}{\sum }_{i=1}^{N}L\left(y_i,f\left(x_i\right)\right)$
  结构风险最小化： ${\min }_{f\in \mathcal{F}}\frac{1}{N}{\sum }_{i=1}^{N}L\left(y_i,f\left(x_i\right)\right)+\lambda J(f)$
  风险最小化策略认为，经验风险（或结构风险）最小的模型就是最优的模型。此时，经验风险函数或结构风险函数就是最优化问题的目标函数。

3. 算法

有了模型、目标函数以及策略，具体求解最优化问题的算法就是统计学习的算法。

三、过拟合与正则化 （Over-fitting and Regularization）

更详细请参考：欠拟合和过拟合以及如何选择模型

1. 过拟合
   样本取值由总体分布决定，但也受随机性的影响。如下图所示，即使“真”模型是一条正弦曲线，样本点也不会全都在此曲线上。所谓“过拟合”就是在训练集里过度追求准确率，导致模型复杂度超过了“真”模型，结果反而“失真”了。因此训练误差并不是越小越好的。
   

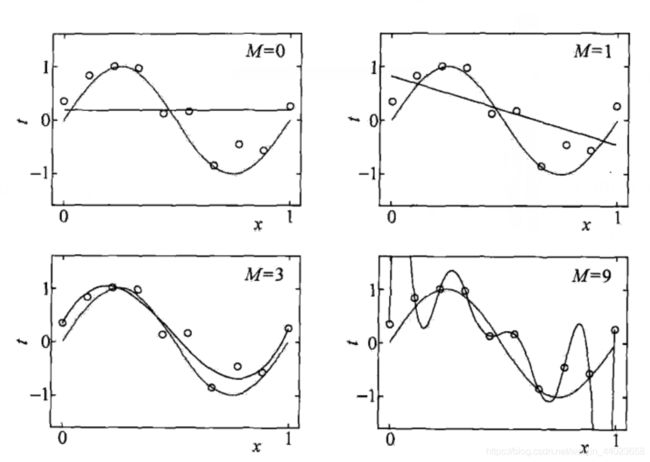
例子：使用最小二乘法拟和曲线

高斯于 1823 年在误差e ${}_1,\dots ,e_n$ 独立同分布的假定下,证明了最小二乘方法的一个最优性质: 在 所有无偏的线性估计类中,最小二乘方法是其中方差最小的！对于数据 $\left(x_i,y_i\right)(i=1,2,3\dots ,m)$

拟合出函数h $(x)$

有误差，即残差: $r_i=h\left(x_i\right)-y_i$

此时L2范数(残差平方和)最小时， $h(x)$ 和 $y$ 相似度最高，更拟合

一般的 $H(x)$ 为n次的多项式， $H(x)=w_0+w_{1}x+w_2{x}^2+\dots w_n{x}^n$
$w\left(w_0,w_1,w_2,\dots ,w_n\right)$ 为参数

最小二乘法就是要找到一组 $w\left(w_0,w_1,w_2,\dots ,w_n\right),$ 使得 ${\sum }_{i=1}^n{\left(h\left(x_i\right)-y_i\right)}^2$ (残差平方和) 最小

即，求 $\min {\sum }_{i=1}^n{\left(h\left(x_i\right)-y_i\right)}^2$

举例：我们用目标函数y = $\sin 2\pi x,$ 加上一个正态分布的噪音干扰，用多项式去拟合

import numpy as np
import scipy as sp
from scipy.optimize import leastsq
import matplotlib.pyplot as plt
%matplotlib inline

ps: numpy.poly $1\mathrm{d}([1,2,3])$ 生成 $1x^2+2x^1+3x^{0\ast }$

# 目标函数
def real_func(x):
    return np.sin(2*np.pi*x)

# 多项式
def fit_func(p, x):
    f = np.poly1d(p)
    return f(x)

# 残差
def residuals_func(p, x, y):
    ret = fit_func(p, x) - y
    return ret

# 十个点
x = np.linspace(0, 1, 10)
x_points = np.linspace(0, 1, 1000)
# 加上正态分布噪音的目标函数的值
y_ = real_func(x)
y = [np.random.normal(0, 0.1) + y1 for y1 in y_]


def fitting(M=0):
    """
    M    为 多项式的次数
    """
    # 随机初始化多项式参数
    p_init = np.random.rand(M + 1)
    # 最小二乘法
    p_lsq = leastsq(residuals_func, p_init, args=(x, y))
    print('Fitting Parameters:', p_lsq[0])

    # 可视化
    plt.plot(x_points, real_func(x_points), label='real')
    plt.plot(x_points, fit_func(p_lsq[0], x_points), label='fitted curve')
    plt.plot(x, y, 'bo', label='noise')
    plt.legend()
    return p_lsq

# M=0
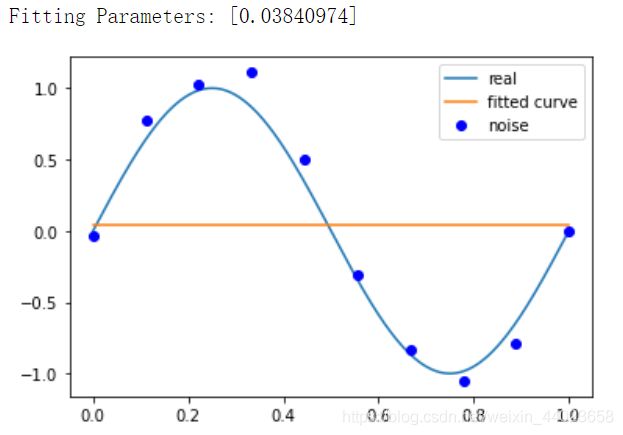
p_lsq_0 = fitting(M=0)

# M=1
p_lsq_1 = fitting(M=1)

# M=3
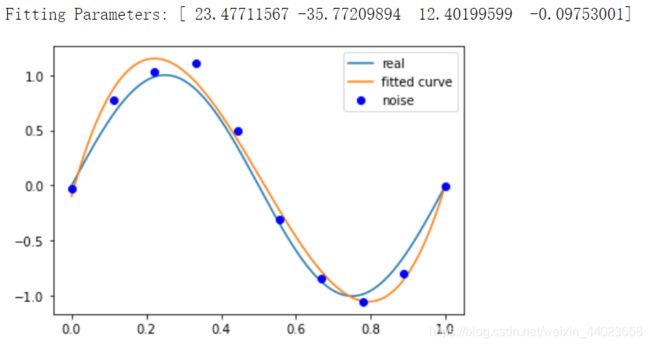
p_lsq_3 = fitting(M=3)

# M=9
p_lsq_9 = fitting(M=9)

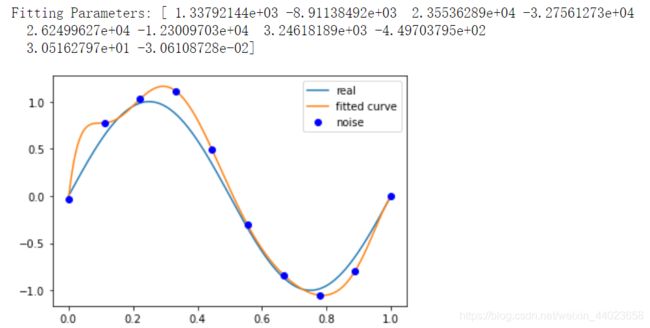
当 M=9 时，多项式曲线通过了每个数据点，但是造成了过拟合

2. 正则化

避免过拟合的方法是正则化，以结构风险代替经验风险。实际上，常用参数向量的L1和L2范数来衡量模型的复杂度。

设模型的参数向量为 $w$

$w$ 的 $L_1$ 范数: $\Vert w{\Vert }_1={\sum }_{i=1}^n\left|w_i\right|,$ 即参数向量各分量的绝对值之和。
$w$ 的 $L_2$ 范数: $\Vert w{\Vert }_2=\sqrt{{\sum }_{i=1}^n{w}_i^2},$ 即参数向量各分量的平方和, $,$ 也就是向量的欧氏长度。

对于线性回归问题, $L_1$ 正则化又称为 “LASSO回归" ， $L_2$ 正则化称为 “岭回归"
简单地说, $L_1$ 正则化使模型的非零参数尽量地少（使得较多的参数归零)， , $L_2$ 正则化则尽量把 参数保留下来。

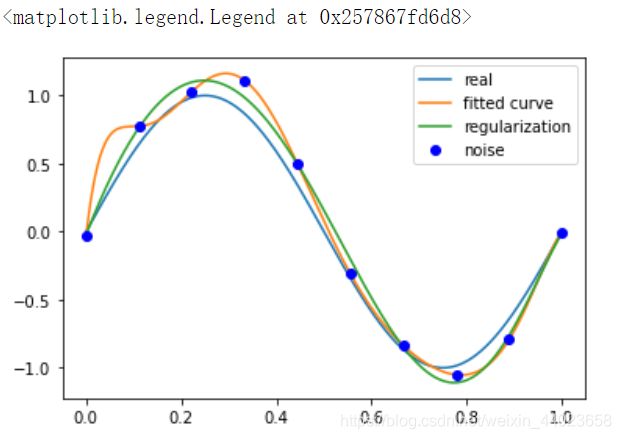
接上面例子结果显示过拟合， 引入正则化项(regularizer)，降低过拟合
$$Q(x)=\sum _{i=1}^n{\left(h\left(x_i\right)-y_i\right)}^2+\lambda \Vert w{\Vert }^2$$
回归问题中，损失函数是平方损失，正则化可以是参数向量的 L2 范数,也可以是 L1 范数。

• L1: regularization*abs§

• L2: 0.5 * regularization * np.square§

regularization = 0.0001
def residuals_func_regularization(p, x, y):
    ret = fit_func(p, x) - y
    ret = np.append(ret,np.sqrt(0.5 * regularization * np.square(p)))  # L2范数作为正则化项
    return ret

# 最小二乘法,加正则化项
p_init = np.random.rand(9 + 1)
p_lsq_regularization = leastsq(
    residuals_func_regularization, p_init, args=(x, y))

plt.plot(x_points, real_func(x_points), label='real')
plt.plot(x_points, fit_func(p_lsq_9[0], x_points), label='fitted curve')
plt.plot(
    x_points,
    fit_func(p_lsq_regularization[0], x_points),
    label='regularization')
plt.plot(x, y, 'bo', label='noise')
plt.legend()

四、泛化能力（Genneralization ability）

所谓“泛化能力”就是通过学习得到的模型，对未知数据的预测能力。通常根据测试误差（在测试集上的表现）来评价泛化能力，但由于测试集的数据有限，可能存在一定的偏差。从理论上来说，我们通过“泛化误差”衡量其泛化能力：

$$R_{exp}(\hat{f})=E_P[L(Y,\hat{f}(X))]={\int }_{\mathcal{X},\mathcal{Y}}L(y,\hat{f}(x))P(x,y)dxdy$$
泛化误差实际上就是模型 $\hat{f}$ 的 “期望风险"

通过研究“泛化误差上界”（generalization error bound）来确定一个模型的泛化能力。泛化上界主要与下列两个因素有关：

• 它是样本容量N的函数，当N趋于无穷，泛化误差上界趋于0；
• 它是假设空间容量的函数，假设空间容量越大（存在越多的假设），寻找合适的模型就越难，泛化误差上界就越大。

在有限假设空间下，定理1.1证明了以上两个结论。

已知训练集 $T=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\dots \left(x_N,y_N\right)\right\},$ T是来自联合概率分布 $\mathrm{P}(\mathrm{X},\mathrm{Y})$ 的独立同分布, $X\in R^n,Y\in \{-1,+1\},$ 假设空间为有限集合 $\mathcal{F}=\left\{f_1,f_2,\dots ,f_d\right\}$

f 的期望风险和经验风险分别为:
$R(f)=E[L(Y,f(X))]$ 和 $\hat{R}(f)=\frac{1}{N}{\sum }_{i=1}^{N}L\left(y_i,f\left(x_i\right)\right)$

定理1.1 对于以上二分类问题, 当假设空间是有限个函数的集合 $\mathcal{F}=\left\{f_1,f_2,\dots ,f_d\right\}$ 时, 对任意一个函数 $f\in \mathcal{F},$ 至少以概率 $1-\delta ,(0<\delta <1)$ 以下不等式成立

$R(f)\le \hat{R}(f)+\epsilon (d,N,\delta ),$ 其中, $\epsilon (d,N,\delta )=\sqrt{\frac{1}{2N}\left(\log d+\log \frac{1}{\delta }\right)}$

结论部分用“概率语言" 表示为 $P(R(f)\le \hat{R}(f)+\epsilon )\ge 1-\delta$,注意此处Iog表示以e为底的自然对数。

证明：(1) Hoeffding不等式 $P(R(f)-\hat{R}(f)\ge \epsilon )\le \exp \left(-2N{\epsilon }^2\right)$

关于Hoeffding不等式的证明, 可以参考林轩田的《Learning from data》，第一章的习题有证明 的提示，这里不深入讨论。

书中式1.34和1.35等价于 $P[|E(\bar{X})-\bar{X}|\ge t]\le \exp \left(-\frac{2N^2{t}^2}{{\sum }_{i=1}^N{\left(b_i-a_i\right)}^2}\right),$ 可通过取绝对值把两个不等式合并，这是Hoeffding不等式的标准形式。

根据定义, $R(f)$ 就是0-1损失函数 $L(Y,f(X))$ 的数学期望, 而 $\hat{R}(f)$ 是损失函数在给定 训练集T下的样本均值。它们分别对应Hoeffding不等式的 $E(\bar{X})$ 和 $\bar{X}$ 。

值得注意的是, 把 $R(f)$ 和 $\hat{R}(f)$ 代入Hoeffding不等式后，绝对值符号消失了。
这意味着 $R(f)-\hat{R}(f)\ge 0?$ 是的，因为 $\hat{R}(f)$ 是在训练集（有限数据集）下的误差, 而 $R(f)$ 是它的数学期望，相当于在无限数据集下的误差。无论模型如何优化，至多使得
常点" 导致 $R(f)-\hat{R}(f)>0$ 。所以不等式中的绝对值号可以去掉。

(2) 如何理解 $P(\exists f\in \mathcal{F}:R(f)-\hat{R}(f)\ge \epsilon )=P\left({\bigcup }_{f\in \mathcal{F}}\{R(f)-\hat{R}(f)\ge \epsilon \}\right)$

注意集合论的基本概念： “事件A、事件B、事件C至少有一个发生” 的概率等于 “事件A发生 或 事件B发生 或 事件C发生" 的概率。

设 $X=\{A,B,C\},$ 则 $P(\exists x\in X)=P(A\cup B\cup C)$,ヨ 表示 “存在一个” , “至少有一个” 的意思, 而 U 表示 “或" 的意思, 因此有
$$P(\exists f\in \mathcal{F}:R(f)-\hat{R}(f)\ge \epsilon )=P\left(\bigcup _{f\in \mathcal{F}}\{R(f)-\hat{R}(f)\ge \epsilon \}\right)$$

根据容斥原理, 等式右侧 $\le {\sum }_{f\in \mathcal{F}}P(R(f)-\hat{R}(f)\ge \epsilon )\le d\exp \left(-2N{\epsilon }^2\right)$

实际上第二个小于等于号的等号不成立，因为一般情况下，不可能所有模型都出现等号（达到上界）。

(3) 从 “至少有一个f" 到 “任意"

把 $d\exp \left(-2N{\epsilon }^2\right)$ 记作 $\delta ,$ 即 $\delta =d\exp \left(-2N{\epsilon }^2\right),$ 可以得到
$$\exp \left(-2N{\epsilon }^2\right)=\frac{\delta }{d}\iff 2N{\epsilon }^2=\log \left(\frac{d}{\delta }\right)\iff {\epsilon }^2=\frac{1}{2N}\log \left(\frac{d}{\delta }\right)=\frac{1}{2N}\left(\log d+\log \frac{1}{\delta }\right)$$

即 $\epsilon (d,N,\delta )=\sqrt{\frac{1}{2N}\left(\log d+\log \frac{1}{\delta }\right)}$

我们已经证明 $P(\exists f\in \mathcal{F}:R(f)-\hat{R}(f)\ge \epsilon )<d\exp \left(-2N{\epsilon }^2\right)=\delta$

设事件 $E=\{\exists f\in \mathcal{F}:R(f)-\hat{R}(f)\ge \epsilon \},$ 则 $P(\bar{E})\ge 1-\delta$

事件E的补集是什么?

回到 $P(\exists x\in X),$ 它的补集为 $P(\overline{A\cup B\cup C})=P(\bar{A}\cap \bar{B}\cap \bar{C}),$ 表示
$\bar{A}、{\bar{B}}_{\text{、 }}\bar{C}$ 同时发生, 它们之中任意一个发生的概率.

所以, $\bar{E}=\{\forall f\in \mathcal{F}:R(f)-\hat{R}(f)<\epsilon \}$

即任意 $f\in \mathcal{F},$ 有 $P(R(f)-\hat{R}(f)<\epsilon )\ge 1-\delta$

不等式左边加上等号概率不变, 即 $P(R(f)-\hat{R}(f)\le \epsilon )\ge 1-\delta ,$ 证毕。

五、监督学习应用

分类问题

引入了precision 精确率（查准率）、recall 召回率（查全率）、F1值等概念：

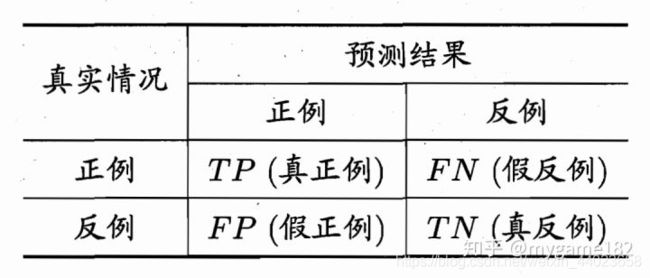
结合信息检索的例子理解P和R？ 一次检索相当于一次预测：
$$P=\frac{TP}{TP+FP}$$
P 表示 “检索出的信息有多少比例是用户感兴趣的" 。在检索出的信息中, 用户感兴趣的是TP, 用户不感兴趣的是FP。 也就是说，预测为正例之中，有多少真实为正? 由此可见, P是从预测 (检 索）的角度定义的概念。
$$R=\frac{TP}{TP+FN}$$
R 表示 “用户感兴趣的信息有多少比例被检索出来" ，在用户感兴趣的信息中，检索出的是TP, 未检索出的是FN。也就是说，真实为正例之中，有多少预测为正? 由此可见，R是从真实（用户） 的角度定义的概念。

从信息检索的角度来看, P翻译为查准率，R翻译为查全率更为合适。

实际上，P和R就好像假设检验中的第一类错误和第二类错误，P和R是相互矛盾的度量。提高查准 率P意味着提高门蓝, 一些真实的正例被拒绝，导致查全率R下降。反之亦然。
$$F1=\frac{2PR}{P+R}=\frac{2TP}{2TP+FP+FN}$$
它是P和R的调和均值, 当F1高时, P和R都较高。

2. 标注问题

标注问题常出现在信息抽取、自然语言处理领域，如：句子中单词词性标注。

3. 回归问题

通过决策函数进行数值预测。

习题

习题1.1
  说明伯努利模型的极大似然估计以及贝叶斯估计中的统计学习方法三要素。伯努利模型是定义在取值为0与1的随机变量上的概率分布。假设观测到伯努利模型n次独立的数据生成结果，其中k次的结果为1，这时可以用极大似然估计或贝叶斯估计来估计结果为1的概率。

解答：

伯努利模型的极大似然估计以及贝叶斯估计中的统计学习方法三要素如下：

1. 极大似然估计
   模型: $\mathcal{F}=\left\{\mathrm{f}\mid {\mathrm{f}}_{\mathrm{p}}(\mathrm{x})={\mathrm{p}}^{\mathrm{x}}(1-\mathrm{p}{)}^{(1-\mathrm{x})}\right\}$
   策略： 最大化似然函数
   $$\text{ 算法: }\arg \underset{\mathrm{p}}{\min }\mathrm{L}(\mathrm{p})=\arg \underset{\mathrm{p}}{\min }\left(\begin{array}{l}\mathrm{n}\\ \mathrm{k}\end{array}\right){\mathrm{p}}^{\mathrm{k}}(1-\mathrm{p}{)}^{(\mathrm{n}-\mathrm{k})}$$
2. 贝叶斯估计
   模型: $\mathcal{F}=\left\{\mathrm{f}\mid {\mathrm{f}}_{\mathrm{p}}(\mathrm{x})={\mathrm{p}}^{\mathrm{x}}(1-\mathrm{p}{)}^{(1-\mathrm{x})}\right\}$
   策略：求参数期望
   算法:
   $$\begin{array}{rl}{\mathrm{E}}_{\pi }\left[\mathrm{p}\mid {\mathrm{y}}_1,\cdots ,{\mathrm{y}}_{\mathrm{n}}\right]& ={\int }_0^1\mathrm{p}\pi \left(\mathrm{p}\mid {\mathrm{y}}_1,\cdots ,{\mathrm{y}}_{\mathrm{n}}\right)\mathrm{d}\mathrm{p}\\ & ={\int }_0^1\mathrm{p}\frac{{\mathrm{f}}_{\mathrm{D}}\left({\mathrm{y}}_1,\cdots ,{\mathrm{y}}_{\mathrm{n}}\mid \mathrm{p}\right)\pi (\mathrm{p})}{{\int }_{\Omega }{\mathrm{f}}_{\mathrm{D}}\left({\mathrm{y}}_1,\cdots ,{\mathrm{y}}_{\mathrm{n}}\mid \mathrm{p}\right)\pi (\mathrm{p})\mathrm{d}\mathrm{p}}\mathrm{d}\mathrm{p}\\ & ={\int }_0^1\frac{{\mathrm{p}}^{\mathrm{k}+1}(1-\mathrm{p}{)}^{(\mathrm{n}-\mathrm{k})}}{{\int }_0^1{\mathrm{p}}^{\mathrm{k}}(1-\mathrm{p}{)}^{(\mathrm{n}-\mathrm{k})}\mathrm{d}\mathrm{p}}\mathrm{d}\mathrm{p}\end{array}$$

伯努利模型的极大似然估计：

定义P $(\mathrm{Y}=1)$ 概率为p，可得似然函数为：
$$\mathrm{L}(\mathrm{p})={\mathrm{f}}_{\mathrm{D}}\left({\mathrm{y}}_1,{\mathrm{y}}_2,\cdots ,{\mathrm{y}}_{\mathrm{n}}\mid \theta \right)=\left(\begin{array}{l}\mathrm{n}\\ \mathrm{k}\end{array}\right){\mathrm{p}}^{\mathrm{k}}(1-\mathrm{p}{)}^{(\mathrm{n}-\mathrm{k})}$$
方程两边同时对p求导, 则：
$$\begin{array}{rl}0& =\left(\begin{array}{l}\mathrm{n}\\ \mathrm{k}\end{array}\right)\left[{\mathrm{k}\mathrm{p}}^{\mathrm{k}-1}(1-\mathrm{p}{)}^{(\mathrm{n}-\mathrm{k})}-(\mathrm{n}-\mathrm{k}){\mathrm{p}}^{\mathrm{k}}(1-\mathrm{p}{)}^{(\mathrm{n}-\mathrm{k}-1)}\right]\\ & =\left(\begin{array}{l}\mathrm{n}\\ \mathrm{k}\end{array}\right)\left[{\mathrm{p}}^{(\mathrm{k}-1)}(1-\mathrm{p}{)}^{(\mathrm{n}-\mathrm{k}-1)}(\mathrm{m}-\mathrm{k}\mathrm{p})\right]\end{array}$$
可解出p的值为p $=0,\mathrm{p}=1,\mathrm{p}=\mathrm{k}/\mathrm{n},$ 显然P $(\mathrm{Y}=1)=\mathrm{p}=\frac{\mathrm{k}}{\mathrm{n}}$

伯努利模型的贝早斯估计： 定义P $(\mathrm{Y}=1)$ 概率为p, $\mathrm{p}在[0,1]$ 之间的取值是等概率的，因此先验概率密度函数 $\pi (\mathrm{p})=1,$ 可得似然函数为：

$$\mathrm{L}(\mathrm{p})={\mathrm{f}}_{\mathrm{D}}\left({\mathrm{y}}_1,{\mathrm{y}}_2,\cdots ,{\mathrm{y}}_{\mathrm{n}}\mid \theta \right)=\left(\begin{array}{l}\mathrm{n}\\ \mathrm{k}\end{array}\right){\mathrm{p}}^{\mathrm{k}}(1-\mathrm{p}{)}^{(\mathrm{n}-\mathrm{k})}$$
根据似然函数和先验概率密度函数, 可以求解p的条件概率密度函数：
$$\begin{array}{rl}\pi \left(\mathrm{p}\mid {\mathrm{y}}_1,\cdots ,{\mathrm{y}}_{\mathrm{n}}\right)& =\frac{{\mathrm{f}}_{\mathrm{D}}\left({\mathrm{y}}_1,\cdots ,{\mathrm{y}}_{\mathrm{n}}\mid \mathrm{p}\right)\pi (\mathrm{p})}{{\int }_{\Omega }{\mathrm{f}}_{\mathrm{D}}\left({\mathrm{y}}_1,\cdots ,{\mathrm{y}}_{\mathrm{n}}\mid \mathrm{p}\right)\pi (\mathrm{p})\mathrm{d}\mathrm{p}}\\ & =\frac{{\mathrm{p}}^{\mathrm{k}}(1-\mathrm{p}{)}^{(\mathrm{n}-\mathrm{k})}}{{\int }_0^1{\mathrm{p}}^{\mathrm{k}}(1-\mathrm{p}{)}^{(\mathrm{n}-\mathrm{k})}\mathrm{d}\mathrm{p}}\\ & =\frac{{\mathrm{p}}^{\mathrm{k}}(1-\mathrm{p}{)}^{(\mathrm{n}-\mathrm{k})}}{\mathrm{B}(\mathrm{k}+1,\mathrm{n}-\mathrm{k}+1)}\end{array}$$
所以p的期望为：
$$\begin{array}{rl}{\mathrm{E}}_{\pi }\left[\mathrm{p}\mid {\mathrm{y}}_1,\cdots ,{\mathrm{y}}_{\mathrm{n}}\right]& =\int \mathrm{p}\pi \left(\mathrm{p}\mid {\mathrm{y}}_1,\cdots ,{\mathrm{y}}_{\mathrm{n}}\right)\mathrm{d}\mathrm{p}\\ & ={\int }_0^1\frac{{\mathrm{p}}^{(\mathrm{k}+1)}(1-\mathrm{p}{)}^{(\mathrm{n}-\mathrm{k})}}{\mathrm{B}(\mathrm{k}+1,\mathrm{n}-\mathrm{k}+1)}\mathrm{d}\mathrm{p}\\ & =\frac{\mathrm{B}(\mathrm{k}+2,\mathrm{n}-\mathrm{k}+1)}{\mathrm{B}(\mathrm{k}+1,\mathrm{n}-\mathrm{k}+1)}\\ & =\frac{\mathrm{k}+1}{\mathrm{n}+2}\end{array}$$

习题1.2
  通过经验风险最小化推导极大似然估计。证明模型是条件概率分布，当损失函数是对数损失函数时，经验风险最小化等价于极大似然估计。

解答：

假设模型的条件概率分布是P ${}_{\theta }(\mathrm{Y}\mid \mathrm{X}),$ 现推导当损失函数是对数损失函数时，极大似然估计等价于经验风险最小化。 极大似然估计的似然函数 为:
$$\mathrm{L}(\theta )=\prod _D{\mathrm{P}}_{\theta }(\mathrm{Y}\mid \mathrm{X})$$
两边取对数：
$$\begin{array}{c}\ln \mathrm{L}(\theta )={\sum }_{\mathrm{D}}\ln {\mathrm{P}}_{\theta }(\mathrm{Y}\mid \mathrm{X})\\ \arg {\max }_{\theta }{\sum }_{\mathrm{D}}\ln {\mathrm{P}}_{\theta }(\mathrm{Y}\mid \mathrm{X})=\arg {\min }_{\theta }{\sum }_{\mathrm{D}}\left(-\ln {\mathrm{P}}_{\theta }(\mathrm{Y}\mid \mathrm{X})\right)\end{array}$$
反之，经验风险最小化等价于极大似然估计，亦可通过经验风险最小化推导极大似然估计。

参考自：
黄海广博士
datawhale