数学建模-层次分析法原理学习笔记

层次分析法简介

• 解决什么问题

  层次分析法（AHP）是一种层次权重决策分析方法。主要是利用较少的定量信息使决策的思维过程数学化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。主要解决评价/决策类问题

• 解决问题前需要思考

  • 评价目标是什么？
  • 有几种可选方案？
  • 评价的准则/标准/指标是什么？

层次分析法步骤

以小明想去旅游作为例子讲解层次分析法的步骤。小明初步选择苏杭、北戴河和桂林三地之一作为目标景点。 请确定评价指标、形成评价体系来为小明同学选择最合适的方案。

建立层次结构模型

• 最高层——决策的目的/目标
  • 小明同学的最佳旅游景点
• 最底层——可选方案
  • 苏杭、北戴河、桂林
• 中间层——评价的准则/标准/指标
  • 景点景色
  • 旅游花费
  • 居住环境
  • 饮食情况
  • 交通便利程

注意：评价的准则/标准/指标需要我们根据题目中的背景材料、常识以及网上搜集到的参考资料进行结合，从中筛选出最合适的指标。优先选择知网（或者万方、百度学术、谷歌学术等平台）搜索相关的文献。

构造两两判断矩阵

• 思路：我们可以让小明填写权重得分表格，计算每个景点的总分，决定最佳景点。
  
• 缺点：因素较多时，直接考虑所有因素的影响可能会顾此失彼、考虑不周全，从而使得最终得到与其实际期望不一致的结果。
• 解决：减少干扰，两两比较，最后推算权重
• 步骤：

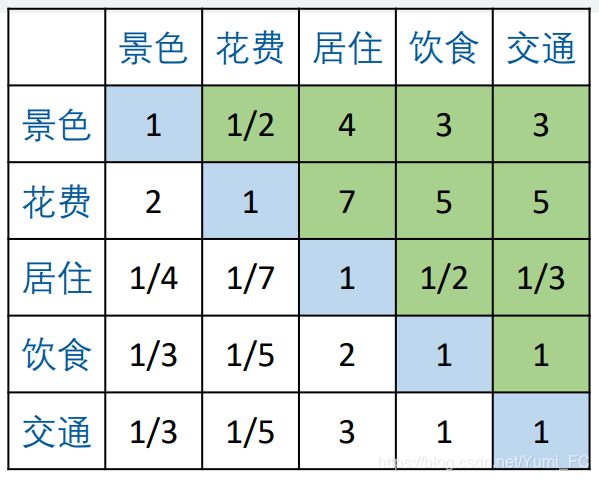
首先，进行评价指标的权重比较

使用Standy的1-9标度方法两两比较

标度	含义
1	表示两个因素相比，具有同样重要性
3	表示两个因素相比，一个因素比另一个因素稍微重要
5	表示两个因素相比，一个因素比另一个因素明显重要
7	表示两个因素相比，一个因素比另一个因素强烈重要
9	表示两个因素相比，一个因素比另一个因素极端重要
2,4,6,8	上述两相邻判断的中值
倒数	A和B相比如果标度为3，那么B和A相比就是1/3

Q1: 根据Standy的1-9标度，请你在选择旅游目的地时，比较景色和花费的重要程度。

A1: 我认为花费比景色略微重要(介于同等重要1和稍微重要3之间吧) 1/2

Q2: 根据Standy的1-9标度，请你在选择旅游目的地时，比较景色和居住的重要程度。

A2: 我认为景色比居住要重要一点(介于稍微重要3和明显重要5之间吧)

小明回答10次（$C_5^2$）后即可得到下表。

$$A=\begin{array}{ccccc}1& \frac{1}{2}& 4& 3& 3\\ 2& 1& 7& 5& 5\\ \frac{1}{4}& \frac{1}{7}& 1& \frac{1}{2}& \frac{1}{3}\\ \frac{1}{3}& \frac{1}{5}& 2& 1& 1\\ \frac{1}{3}& \frac{1}{5}& 3& 1& 1\end{array}$$
该矩阵即为判断矩阵，有以下特点：

1. $a_{ij}$表示的意义是，与指标j相比，i的重要程度
2. 当i=j时，两个指标相同，因此同等重要记为1，这就解释了主对角线元素为1
3. $a_{ij}>0$且满足$a_{ij}\ast a_{ji}=1$ （我们称满足这一条件的矩阵为正互反矩阵）

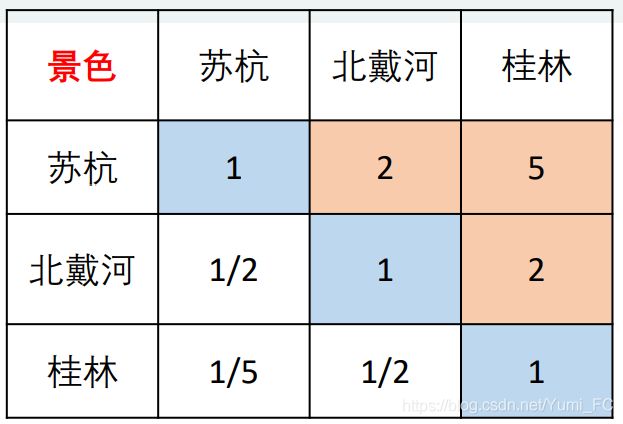
其次，两两比较方案的权重

Q1：你觉得苏杭的风景和北戴河相比如何？

A1：稍微好一点点吧（介于1‐3之间）

Q2：你觉得苏杭的风景和桂林相比如何？

A2：要明显的好哦（5）

Q3：你觉得北戴河的风景和桂林相比如何？

A3：稍微好一点点吧（介于1‐3之间

注意：判断矩阵中的元素只能是1至9和它们的倒数，有些文章中填入了其他的数（例如3/2、5/4），这是不可以的。

一致性检验

• 为什么要进行一致性检验

填表有可能出现不一致的情况，如下图

假设苏杭为A，北戴河为B，桂林为C。按上表可知，苏杭比北戴河景色好一点，即A > B；苏杭和桂林景色一样好，即A = C；北戴河比桂林景色好一点，即B > C。出现了矛盾/不一致现象。

一致矩阵不需要一致性检验，只有非一致矩阵的判断矩阵才需要一致性检验

• 什么样的矩阵是一致矩阵

$a_{ij}=\frac{i的重要程度}{j的重要程度}，a_{jk}=\frac{j的重要程度}{k的重要程度}$

$a_{ik}=\frac{i的重要程度}{k的重要程度}=a_{ij}\ast a_{jk}$

例如

$a_{桂林-苏杭}=\frac{桂林相对苏杭的重要程度}{苏杭相对苏杭的重要程度}=\frac{4}{1}=4$

$a_{苏杭-北戴河}=\frac{苏杭相对北戴河的重要程度}{北戴河相对北戴河的重要程度}=\frac{\frac{1}{2}}{1}=\frac{1}{2}$

$a_{桂林-北戴河}=\frac{桂林相对北戴河的重要程度}{北戴河相对北戴河的重要程度}=\frac{2}{1}=2=4\ast \frac{1}{2}$

一致矩阵特点：各行（各列）之间成倍数关系

• 小结

1. 若矩阵中每个元素$a_{ij}>0$且满足$a_{ij}\ast a_{ji}=1$ ，则我们称满足这一条件的矩阵为正互反矩阵
2. 在层次分析法中，我们构造的判断矩阵均是正互反矩阵
3. 若正互反矩阵满足$a_{ik}=a_{ij}\ast a_{jk}$（各行/列之间成倍数关系），我们则称其为一致矩阵

注意：基于第一点原因，我们在使用判断矩阵求权重之前，必须对其进行一致性检验。来检验我们构造的判断矩阵和一致矩阵是否有太大的差别（在一定范围内就可以）

• 一致性检验的步骤

1.计算一致性指标CI

$$CI=\frac{{\lambda }_{max}-n}{n-1}$$

${\lambda }_{max}$为n阶正互反矩阵A的最大特征值

n阶正互反矩阵A为一致矩阵时当且仅当最大特征值${\lambda }_{max}=n$

当正互反矩阵A非一致时，一定满足${\lambda }_{max}>n$

判断矩阵越不一致时，最大特征值与n相差就越大

特征值可用matlab软件进行计算。

如果特征值中有虚数，则比较的是特征值的模长。

2.查找对应的平均随机一致性指标RI

查表即可

3.计算一致性比例CR

$$CR=\frac{CI}{RI}$$

如果$CR<0.1$， 则可认为判断矩阵的一致性可以接受；否则需要对判断矩阵进行修正。

修改判断矩阵A，往一致矩阵上修改即可

一致矩阵计算权重

方法一：使用算数平均数求权重

• 使用第一列计算出来的权重

$$苏杭=\frac{1}{(1+\frac{1}{2}+\frac{1}{5})}=0.5882$$

$$北戴河=\frac{\frac{1}{2}}{(1+\frac{1}{2}+\frac{1}{5})}=0.2941$$

$$桂林=\frac{\frac{1}{5}}{(1+\frac{1}{2}+\frac{1}{5})}=0.1177$$

• 使用第二列计算出来的权重

$$苏杭=\frac{2}{(2+1+\frac{1}{2})}=0.5714$$

$$北戴河=\frac{1}{(2+1+\frac{1}{2})}=0.2857$$

$$桂林=\frac{\frac{1}{2}}{(2+1+\frac{1}{2})}=0.1429$$

• 使用第三列计算出来的权重

$$苏杭=\frac{5}{(5+2+1)}=0.625$$

$$北戴河=\frac{2}{(5+2+1)}=0.25$$

$$桂林=\frac{1}{(5+2+1)}=0.125$$

• 综合计算

$$苏杭=\frac{(0.5882+0.5714+0.625)}{3}=0.5949$$

$$北戴河=\frac{(0.2941+0.2857+0.25)}{3}=0.2766$$

$$桂林=\frac{(0.1177+0.1429+0.125)}{3}=0.1285$$

方法二：几何平均数求权重

方法三：特征值法求权重

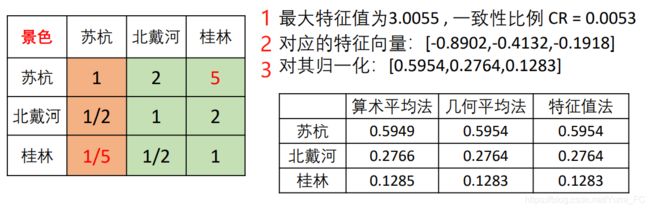
一致矩阵有一个特征向量n，其余特征值为0。

另外，我们很容易得到，特征值为n时，对应的特征向量为$k[\frac{1}{a_{11}},\frac{1}{a_{12}}，\dots ,\frac{1}{a_{1n}}{]}^T(k\ne 0)$

这一特征向量刚好就是一致矩阵的第一列

最后进行归一化（即$\frac{-0.8902}{-0.8902+(-0.4132)+(-0.1918)}=0.5954$）

最后汇总结果得到权重矩阵

计算各方案总分

$苏杭=0.2636\ast 0.5954+0.4758\ast 0.0819+0.0538\ast 0.4286+0.0981\ast 0.6337\ast 0.1087\ast 0.1667=0.299$

$北戴河=0.2636\ast 0.2764+0.4758\ast 0.2363+0.0538\ast 0.4286+0.0981\ast 0.1919\ast 0.1087\ast 0.1667=0.245$

$桂林=0.2636\ast 0.1283+0.4758\ast 0.6817+0.0538\ast 0.1429+0.0981\ast 0.1744\ast 0.1087\ast 0.6667=0.455$

所以最佳旅游地点为桂林