Neat算法讲解（遗传拓扑神经网络）

Neat算法讲解（遗传拓扑神经网络的原理）

  遗传算法是个通用的框架，因此需要根据具体的问题来定义遗传算法。
  整体框架可分为三部分：交叉、变异与适应度。不过虽然整体的流程是一致的，但是因为问题不同，我们定义的基因也有所不同，那交叉与变异也会随之变化。
  这篇论文将神经元及其连接定义成基因组
  而遗传演化神经网络论文是将网络层及其学习率定义为基因组，遗传算法是解决一般性问题的通用框架，就是因为我们可以根据问题去定义基因组。

算法核心：超参数设置

  整体框架可分为三部分：交叉、变异与适应度。
  1、超参数设置，个体基因：（节点连接与节点类型）；种群规模：150；物种划分：基于权值相似度划分物种。

伪代码：

while condition:
	if random.random < 交叉率:
		选择操作（适应度越高，越容易被选中）
		物种内交叉
		if random.random < 变异率:
			变异操作
		评估适应度
else:		#（random.random > 交叉率）直接变异
	if random.random < 变异率:
		变异操作
	评估适应度
	# 淘汰操作
	每个物种保留一定数量的个体
	if random.random < 灭绝率:
		灭绝最差的物种
		种群间的物种交叉生成新的子代

condition: 迭代次数 or fitness达到设定的阈值
评估适应度: fitness = 1/（训练集的误差）^2
这里的适应度函数是自定义的

算法核心：交叉操作

  论文通过一个链表定义基因的节点连接，选择两个个体进行交叉的时候，按照链表的顺序，逐一操作，最后生成新的子代

算法核心：变异操作

  变异操作也是在链表中进行，且会有两种变异：增加网络连接和增加网络节点

conda软件版本

python = 3.7.7
pandas = 1.0.3
neat-python = 0.92
numpy = 1.17.0
matplotlib = 3.1.1
conda install graphviz = 2.38.0
pip install graphviz = 0.13.2

NEAT实验例子：训练一个XOR网络

伪代码：

异或：输入相异，输出为1，输入相同，输出为0

xor_inputs = [(0.0, 0.0), (0.0, 1.0), (1.0, 0.0), (1.0, 1.0)]
xor_outputs = [(0.0,), (1.0,), (1.0,), (0.0,)]

NEAT配置文件（删除后面#的注释，保存为：config-feedforward）

  [NEAT]  
  fitness_criterion     = max  
  fitness_threshold     = 3.9  # 适应度的阈值  
  pop_size              = 150  # 种群规模  
  reset_on_extinction   = False  
    
  [DefaultGenome]  
  # node activation options  # 节点的激励函数  （一般默认）
  activation_default      = sigmoid  
  activation_mutate_rate  = 0.0  
  activation_options      = sigmoid  
    
  # node aggregation options  # 节点的聚合选择 （一般默认）  
  aggregation_default     = sum  
  aggregation_mutate_rate = 0.0  
  aggregation_options     = sum  
    
  # node bias options  # 节点的偏置选择  
  bias_init_mean          = 0.0  
  bias_init_stdev         = 1.0  
  bias_max_value          = 30.0  
  bias_min_value          = -30.0  
  bias_mutate_power       = 0.5  
  bias_mutate_rate        = 0.7  
  bias_replace_rate       = 0.1  
   
  # genome compatibility options  # 基因组兼容性选项 
  compatibility_disjoint_coefficient = 1.0  	#	兼容性不相交系数
  compatibility_weight_coefficient   = 0.5  	#	兼容性权重系数
    
  # connection add/remove rates  # 连接增加/删除的概率
  conn_add_prob           = 0.5  #	概率
  conn_delete_prob        = 0.5  
     
  # connection enable options  
  enabled_default         = True  
  enabled_mutate_rate     = 0.01  
    
  feed_forward            = True  # 是否加入RNN神经元 （循环神经网络）
  initial_connection      = full  #	初始连接全连接
    
  # node add/remove rates  # 结点的添加和删除概率  
  node_add_prob           = 0.2  
  node_delete_prob        = 0.2  
    
  # network parameters  # 输入层、输出层、隐藏层的神经元个数  
  num_hidden              = 2  
  num_inputs              = 2  
  num_outputs             = 1  
    
  # node response options  # 节点相应选项
  response_init_mean      = 1.0  
  response_init_stdev     = 0.0  
  response_max_value      = 30.0  
  response_min_value      = -30.0  
  response_mutate_power   = 0.0  
  response_mutate_rate    = 0.0  
  response_replace_rate   = 0.0  
    
  # connection weight options # 连接权重选项 
  weight_init_mean        = 0.0  
  weight_init_stdev       = 1.0  
  weight_max_value        = 30  
  weight_min_value        = -30  
  weight_mutate_power     = 0.5  
  weight_mutate_rate      = 0.8  
  weight_replace_rate     = 0.1  
    
  [DefaultSpeciesSet]    
  # genomic distance小于此距离被认为是同一物种  
  compatibility_threshold = 3.0   #	兼容性阈值
   
  [DefaultStagnation]  #	默认停滞
  species_fitness_func = max  
  max_stagnation       = 20  
  species_elitism      = 2  #	物种精英
   
  [DefaultReproduction]  	#	默认繁殖
  elitism            = 2   # 保留最优的个体遗传到下一代的个数  
  survival_threshold = 0.2  # 每一代每个物种的存活率  

主函数代码：（保存为：run.py）

import os
import neat
import visualize

# 2个输入，1个输出的异或实验
xor_inputs = [(0.0, 0.0), (0.0, 1.0), (1.0, 0.0), (1.0, 1.0)]
xor_outputs = [(0.0,), (1.0,), (1.0,), (0.0,)]


def eval_genomes(genomes, config):
    # 评估函数
    for genome_id, genome in genomes:  # 每一个个体
        genome.fitness = 4.0  # 适应度为4.0的评估，因为有4个结果全部猜对
        net = neat.nn.FeedForwardNetwork.create(genome, config)  # 生成一个网络
        for xi, xo in zip(xor_inputs, xor_outputs):  # 把它丢进去训练
            output = net.activate(xi)
            genome.fitness -= (output[0] - xo[0]) ** 2  # 训练完后得到一个fitness


def run(config_file):
    # 读取配置文件
    config = neat.Config(neat.DefaultGenome, neat.DefaultReproduction,
                         neat.DefaultSpeciesSet, neat.DefaultStagnation,
                         config_file)

    # 创建种群
    p = neat.Population(config)

    # 打印训练过程
    p.add_reporter(neat.StdOutReporter(True))
    stats = neat.StatisticsReporter()
    p.add_reporter(stats)
    p.add_reporter(neat.Checkpointer(50))

    # 迭代300次
    winner = p.run(eval_genomes, 300)

    # 显示最佳网络
    print('\nBest genome:\n{!s}'.format(winner))
    print('\nOutput:')
    winner_net = neat.nn.FeedForwardNetwork.create(winner, config)
    for xi, xo in zip(xor_inputs, xor_outputs):
        output = winner_net.activate(xi)
        print("input {!r}, expected output {!r}, got {!r}".format(xi, xo, output))

    # 打印网络结构
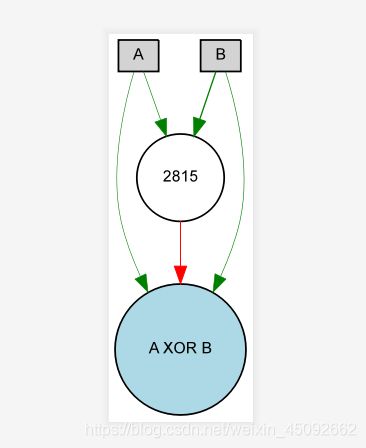
    node_names = {-1: 'A', -2: 'B', 0: 'A XOR B'}
    visualize.draw_net(config, winner, True, node_names=node_names)
    visualize.plot_stats(stats, ylog=False, view=True)
    visualize.plot_species(stats, view=True)

    p = neat.Checkpointer.restore_checkpoint('neat-checkpoint-49')
    p.run(eval_genomes, 10)


if __name__ == '__main__':
    local_dir = os.path.dirname(__file__)
    config_path = os.path.join(local_dir, 'config-feedforward')
    run(config_path)

实验结果：

  生成的.svg后缀文件用浏览器就可以打开，实验结果显示的是遗传拓扑神经网络的结构图与其fitness趋势。

图1.1 网络结构图

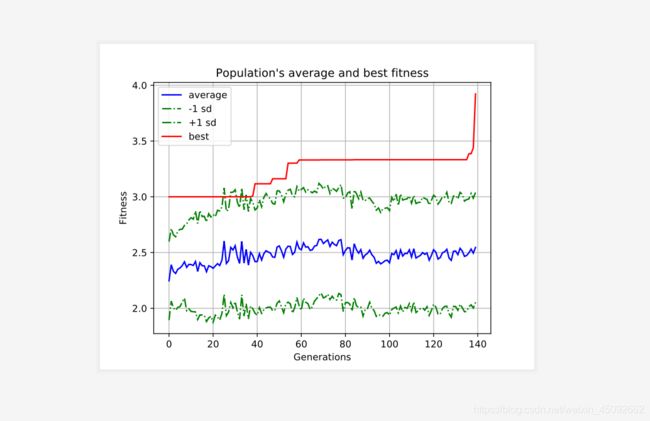
图1.2 fitness趋势图

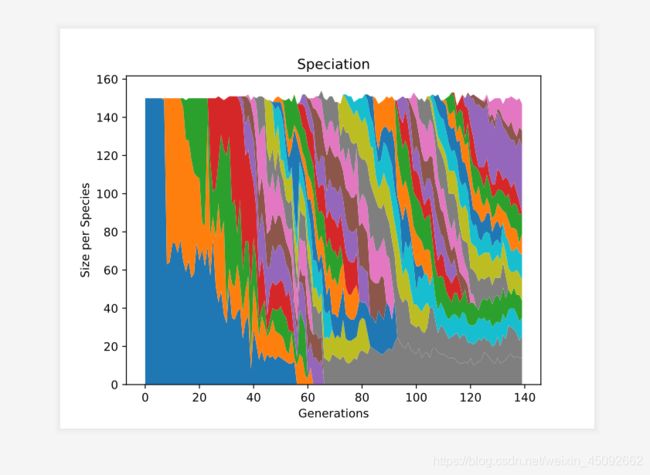
图1.3 物种形成变化图

实验结果：

****** Running generation 139 ****** 

Population's average fitness: 2.54573 stdev: 0.49305
Best fitness: 3.92277 - size: (2, 5) - species 30 - id 18565

Best individual in generation 139 meets fitness threshold - complexity: (2, 5)

Best genome:
Key: 18565
Fitness: 3.9227726535092953
Nodes:
	0 DefaultNodeGene(key=0, bias=-0.36935409061892416, response=1.0, activation=sigmoid, aggregation=sum)
	2815 DefaultNodeGene(key=2815, bias=-4.043413198029619, response=1.0, activation=sigmoid, aggregation=sum)
Connections:
	DefaultConnectionGene(key=(-2, 0), weight=1.2407529943809679, enabled=True)
	DefaultConnectionGene(key=(-2, 2815), weight=3.280828495015102, enabled=True)
	DefaultConnectionGene(key=(-1, 0), weight=1.094918491185449, enabled=True)
	DefaultConnectionGene(key=(-1, 2815), weight=1.2692785642422044, enabled=True)
	DefaultConnectionGene(key=(2815, 0), weight=-2.3709331394024136, enabled=True)

# 解释：node_names = {-1: 'A', -2: 'B', 0: 'A XOR B'}，2815:’中间一个节点’

Output:
input (0.0, 0.0), expected output (0.0,), got [0.1362525265929158]
input (0.0, 1.0), expected output (1.0,), got [0.9837112565200653]
input (1.0, 0.0), expected output (1.0,), got [0.9741136148621398]
input (1.0, 1.0), expected output (0.0,), got [0.2402647859926438]
Mean genetic distance 3.212, standard deviation 1.097
Mean genetic distance 3.247, standard deviation 1.132
Mean genetic distance 3.161, standard deviation 1.000
Mean genetic distance 3.032, standard deviation 0.971
Mean genetic distance 3.048, standard deviation 1.073
Mean genetic distance 3.139, standard deviation 1.137
Mean genetic distance 3.057, standard deviation 1.185
Mean genetic distance 3.005, standard deviation 1.135
Mean genetic distance 3.010, standard deviation 1.097
Mean genetic distance 3.049, standard deviation 1.195

所有代码和结果在我的码云里
https://gitee.com/rengarwang/neat_XOR

附加，RNN（循环神经网络）讲解：

  神经网络可以当做是能够拟合任意函数的黑盒子，只要训练数据足够，给定特定的x，就能得到希望的y

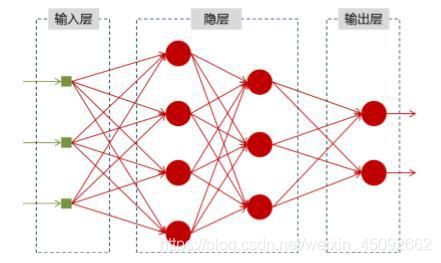
  将神经网络模型训练好之后，在输入层给定一个x，通过网络之后就能够在输出层得到特定的y，那么既然有了这么强大的模型，为什么还需要RNN（循环神经网络）呢？
  他们都只能单独的处理一个个的输入，前一个输入和后一个输入是完全没有关系的。但是，某些任务需要能够更好的处理序列的信息，即前面的输入和后面的输入是有关系的。
  比如，当我们在理解一句话的意思时，孤立的理解这句话的每个词是不够的，我们需要处理这些词连接起来的整个序列；当我们处理视频的时候，我们也不能只单独的去分析每一帧，而要分析这些帧连接起来的整个序列。
  RNN结构，一个简单的循环神经网络，

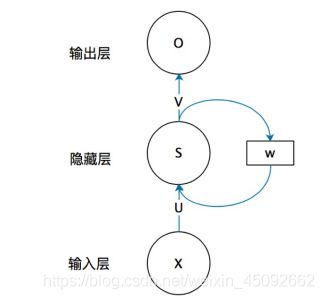
  如果把上面有W的那个带箭头的圈去掉，它就变成了最普通的全连接神经网络。x是一个向量，它表示输入层的值（这里面没有画出来表示神经元节点的圆圈）；s是一个向量，它表示隐藏层的值（这里隐藏层面画了一个节点，你也可以想象这一层其实是多个节点，节点数与向量s的维度相同）；U是输入层到隐藏层的权重矩阵，o也是一个向量，它表示输出层的值；V是隐藏层到输出层的权重矩阵。那么，现在我们来看看W是什么。循环神经网络的隐藏层的值s不仅仅取决于当前这次的输入x，还取决于上一次隐藏层的值s。权重矩阵 W就是隐藏层上一次的值作为这一次的输入的权重。

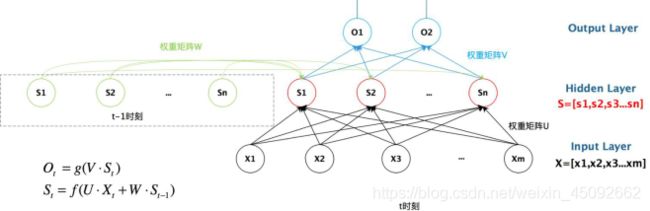
  从上图就能够看到，上一时刻的隐藏层是如何影响当前时刻的隐藏层的。
  如果把上面的图展开，循环神经网络也可以成下面这个样子：

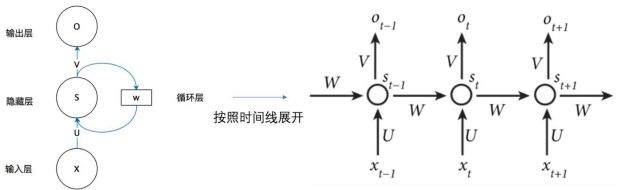
  这个网络在t时刻接收到输入 之后，隐藏层的值是 ，输出值是 。关键一点是， 的值不仅仅取决于 ，还取决于 。我们可以用下面的公式来表示循环神经网络的计算方法：

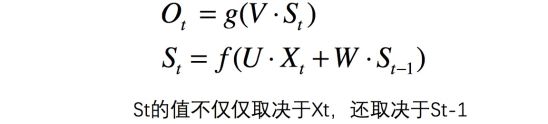
  为了简单说明问题，偏置都没有包含在公式里面。