计算几何总结
计算几何总结
题目叫计算几何总结,其实是我也是刚刚接触不及。虽然,以前大一省赛集训的时候被学长分配去负责计算几何了,但是那时候由于知识面比较的窄。当时,也没学到太多的东西,只是学会了一点基础的几何知识,这次趁着寒假集训想从新学学几何。以后,这个总结的内容会逐渐增多的,敬请期待吧。
线性、离散啥的考试都弱爆了,继续刷题去。
计算几何的知识点有很多,如果想出简单的话,可以就是一个模板的问题。但是如果,要出难得时候也是一个头痛的问题。但是可以一点一滴的积累。
先来看一下计算几何的基础知识,叉积的运用吧。
如果,学过线性代数的知识后,大家就可以很容易的理解了。现在我就运用线性代数的之后给大家解释一下叉积的本质吧。

![]()
则叉积就为:
Area = (x1*y2*1+y1*x3*1+1*x2*y3-1*y2*x3-x1*1*y3-y1*x2*1)/2;
实践是检验真理的唯一标准,开始做题吧。
以下有些知识是参考他人博客。
一、 求解多边形中心问题。
1. 1 累加和求重心
设平面上有N 个离散数据点( xi , yi ) ( i = 1, 2, ., n) , 其
多边形重心G( . x1, . y1) 为:

这是求多边形最简单直观的方法。可以直接利用离散数
据点的x, y坐标就能求图形重心。但是缺陷在于没有对离散
数据点所围图形做任何处理和分析,精度不够。
1. 2 算法一:在讲该算法时,先要明白下面几个定理。
定理1 已知三角形△A1A2A3的顶点坐标Ai ( xi , yi ) ( i =1, 2, 3) 。它的重心坐标为:
xg = (x1+x2+x3) / 3 ; yg = (y1+y2+y3) / 3 ;
定理2 已知三角形△A1A2A3的顶点坐标Ai ( xi , yi ) ( i =1, 2, 3) 。该三角形的面积为:
S = ( (x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1) ) / 2 ;
△A1A2A3 边界构成逆时针回路时取+ , 顺时针时取 -。
另外在求解的过程中,不需要考虑点的输入顺序是顺时针还是逆时针,相除后就抵消了。
原理:将多边形划分成n个小区域, 每个小区域面积为σi ,重心为Gi ( . xi , . yi ) ,利用求平面薄板重心公式把积分变
成累加和:
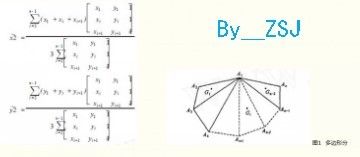
在运用的时候一般是把分母中的3提出来放到最后的结果中在除以3就好了,不要问我为什么。这个问题可以去问一下你小学数学老师。
运用模板刷刷题吧~
题目链接Click Here~
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
struct Point{double x,y;};
//叉积求面积
double Area(const Point p0,const Point p1,const Point p2)
{
// 另外在求解的过程中,不需要考虑点的输入顺序是顺时针还是逆时针,相除后就抵消了。
return (p0.x*p1.y+p1.x*p2.y+p2.x*p0.y-p1.x*p0.y-p2.x*p1.y-p0.x*p2.y)/2.0;
}
int main()
{
int T,n;
scanf("%d",&T);
while(T--)
{
Point p0,p1,p2;
double area = 0,suma = 0,sumx = 0,sumy = 0;
scanf("%d",&n);
scanf("%lf%lf",&p0.x,&p0.y);
scanf("%lf%lf",&p1.x,&p1.y);
for(int i = 2;i < n;++i)
{
scanf("%lf%lf",&p2.x,&p2.y);
area = Area(p0,p1,p2);
suma += area;
sumx += (p0.x+p1.x+p2.x)*area;
sumy += (p0.y+p1.y+p2.y)*area;
p1 = p2;
}
printf("%.2lf %.2lf\n",sumx/suma/3,sumy/suma/3);
}
return 0;
}