几种GNN模型的应用与改进

[学习笔记(1)]深入浅出了解GCN原理(公式+代码)
[学习笔记(2)]深入浅出了解GNN的几种变体
[学习笔记(3)]几种GNN模型的应用与改进

前言

关于图的文章，大体上都是在解决一个问题，就是如何从大规模图数据中，有效嵌入节点和拓扑结构的信息，同时降低计算的复杂度，缓解过拟合的风险。有效地对图结构数据的节点进行embedding就需要考虑数据本身的特征，同时也要考虑不同应用场景以及下游任务的目标。接下来，笔者挑了近期看的几篇有意思的GNN文章做简短的描述和思考，文中只列出必要的公式做辅助说明，详细公式推导读者可以自行查阅知乎或者阅读原文与原代码。
笔者水平有限，如有错误，还望各位读者望积极指正。

  在实际场景中，图数据本身就是错综复杂的，节点直接的联系有些是我们可以从先验知识中得到的，有些是无法直接定义，或者需要从模型中隐式地学习。关于图的描述和学习就有很多方法，比如从邻近采样有deepwalk、Node2Vec、mate-path等，节点的聚合有 GraphSAGE、Attention等，相似度衡量有欧式距离、KL散度、余弦距离等等，从拓扑图的结构出发，又要考虑有向图、异构图和动态图。有向图比如DGP，异构图又有Graph Inception 和HAN，考虑边的异构性有G2S和R-GCN等，考虑动态图又有DCRNN、ST-GCN、Structural-RNN等等，在比如从训练方式上还分别有监督、无监督（GAE、VGAE）、自监督等方式。

关系图

R-GCN（Modeling Relational Data with Graph Convolutional Networks Michael）：

  在上一篇文章[1]中，已经简短介绍过，作者首次将GCN运用到关系型数据，对于不同边的关系用$W_r$进行了映射，相同一组的relationship共享权重，并基于这样的网络，可进行实体分类（Entity classificatio）与边关系预测（Link prediction）任务。
$$h_i^{i+1}=\sigma (\sum _{r\in \mathcal{R}}\sum _{j\in {\mathcal{N}}_i^r}\frac{1}{c_{i,r}}{W}_r^{(l)}{h}_j^{(l)}+W_0^{(l)}{h}_i^{(l)})(1)$$

• ${\mathcal{N}}_i^r$表示与节点$v_i$具有$r$关系的邻居节点集合
• $c_{i,r}$是归一化因子，可学习也可自行设定，如$c_{i,r}=|{\mathcal{N}}_i^{(r)}|$
  

Fig1 R-GCN模型中跟新单个节点实体(红色)的示意图

思考

  R-GCN可以端到端地训练并有效用于下游任务如实体分类和关系预测，并首次尝试用于关系型数据，对于不同的关系以及不同方向的关系，都会学习一个参数矩阵$W_r$，但是考虑边的关系需要一些先验知识，一些隐式边的关系可能就无法知道和预测,另外如果遇到多个超级节点（度大节点），也会导致学习参数过大，模型过拟合等问题。

VGAE（Variational graph auto-encoders）

  这是一篇发表在NIPS2016上的经典图自编码器文章，作者将变分自编码器（Variational Auto-Encoders）的思想迁移到了图结构数据上，用已知的拓扑图关系经过编码器（图卷积）学到节点向量表示的分布$\mu ,\sigma$，在分布中采样得到节点的向量表示，然后进行解码器（链路预测）重新构建图。模型的优化目标如公式（2）所示。
$$\mathcal{L}={\mathbb{E}}_{q(Z|X,A)}[lo{g}_p(A|Z)]-KL[q(Z|X,A)||p(Z)](2)$$
其中${\mathbb{E}}_{q(Z|X,A)}[lo{g}_p(A|Z)]$度量生成图和原始图之间的距离，可以用对应节点的交叉熵来表示。

Fig2 变分自编码器（图片来源知乎）

训练过程中，为了使生成器生成效果最佳，模型会趋向于把方差值学习为0，这样从正态分布中采样出来的是定值，有利于减小生成样本和真实样本之间的差异。但这样模型就退化成了普通的自编码器，无法推断出一些图中可能未标明的隐式边关系。所以为了解决这个问题，在损失函数中加入各个独立正态分布和标准正态分布的KL散度，强迫模型将学习到的分布趋近于标准正太分布。
$$\begin{gathered} -D_{KL}(q(z|x^{(i)})||p(z))=\int q_{\varphi }(z|x)log\frac{p(z)}{q_{\varphi }(z|x)}dz \\ =\int q_{\varphi }(z|x)logp(z)dz-\int q_{\varphi }(z|x)log{q}_{\varphi }(z|x)dz \end{gathered}$$

公式（3）KL散度定义

左边相当于正太的分布求标准分布的期望：
$$\begin{gathered} left=\int N(z;\mu ,{\sigma }^2)logN(z;0,1)dz \\ =E_{z\sim N(\mu ,{\sigma }^2)}[logN(z;0,1)] \\ =E_{z\sim N(\mu ,{\sigma }^2)}[log(\frac{1}{\sqrt{2\pi }}{e}^{\frac{(z{)}^2}{2}})] \\ =-\frac{1}{2}log2\pi -\frac{1}{2}{E}_{z\sim N(\mu ,{\sigma }^2)}[z^2](平方的期望) \\ =-\frac{1}{2}log2\pi -\frac{1}{2}({\mu }^2+{\sigma }^2) \end{gathered}$$

公式（4）KL散度左半部分

右半部分：

$$\begin{gathered} right=\int N(z;\mu ,{\sigma }^2)logN(z;\mu ,{\sigma }^2)dz \\ =E_{z\sim N(\mu ,{\sigma }^2)}[logN(z;u,{\sigma }^2)] \\ =E_{z\sim N(\mu ,{\sigma }^2)}[log(\frac{1}{\sqrt{2\pi }\sigma }{e}^{\frac{(z-\mu {)}^2}{2{\sigma }^2}})] \\ =-\frac{1}{2}log2\pi -\frac{1}{2}log{\sigma }^2-\frac{1}{2{\sigma }^2}{E}_{z\sim N(\mu ,{\sigma }^2)}[(z-\mu {)}^2] \\ =-\frac{1}{2}log2\pi -\frac{1}{2}(log{\sigma }^2+1) \end{gathered}$$

公式（5）KL散度右半部分

最终KL散度部分可以简化为下式：
$${\mathcal{L}}_{\mu ,{\sigma }^2}=1/2\sum _i^N(1+log({\sigma }_i^2)-{\mu }_i^2-{\sigma }_i^2)(6)$$
不熟悉变分自编码器的读者可先阅读Auto-Encoding Variational Bayes
损失函数部分的代码如下：

import torch
import torch.nn.modules.loss
import torch.nn.functional as F

def loss_function(preds, labels, mu, logvar, n_nodes, norm, pos_weight):
    cost = norm * F.binary_cross_entropy_with_logits(preds, labels, pos_weight=pos_weight)

    # see Appendix B from VAE paper:
    # Kingma and Welling. Auto-Encoding Variational Bayes. ICLR, 2014
    # https://arxiv.org/abs/1312.6114
    # 0.5 * sum(1 + log(sigma^2) - mu^2 - sigma^2)
    KLD = -0.5 / n_nodes * torch.mean(torch.sum(
        1 + 2 * logvar - mu.pow(2) - logvar.exp().pow(2), 1))
    return cost + KLD

由于采样编码器的分布是无法参与梯度下降的计算的，这里作者使用了一个trick，先用标准正太分布采样$\epsilon$，在通过$Z=\mu +\epsilon \ast \sigma$得到$Z\sim N(\mu ,{\sigma }^2)$，另外一个trick就是参数共享，生成$\mu$和$\sigma$是同一个隐藏层的输出。

  在实际任务训练中，只保留一部分边的关系进行训练，随机mask一部分边，同时从负样本中随机进行采样，计算loss的时候利用mask机制只计算有监督信息的点的loss。通过这样的方式训练出的模型参数，就能预测出之前mask的节点之间是否存在关系，同时也能预测出没有监督信息的点之间是否存在边。

思考

  笔者亲测了模型的代码，使用的是cora数据集，AUC准确率能达到93左右，比文章中实验的结果还要好一些，但是发现源代码中验证集中计算的边，在测试集中也出现过，所以可能会存在标签泄露问题，同时训练过程中，loss部分只计算了正样本，也就是有标签的部分，对于负样本并没有计算，这使得模型在训练过程中，只趋向于预测原有的图关系，即验证集和训练集中的标注边，而对未标注的图关系趋向于预测为0，所以AUC指标并不能反应模型对隐式边关系有很好的预测能力，只能表现为复原后的图结构与原始结构的相似度。

异构图

Variational graph auto-encoders for miRNA-disease association prediction

  最近一篇发表在Methods上的运用VAGE的文章，作者将VAGE运用在了疾病与micRNA关系的预测上，感觉还挺有意思的。

Fig3 micRNA-disease 异构网络与子网络

不同的是，文中的网络是包含两个子网络的异构网络，两个子网络分别是micRNA之间的关系，以及疾病之间的关系。同时在两个子网络之间又有相互的关系。

Fig4 micRNA-disease 异构网络与子网络

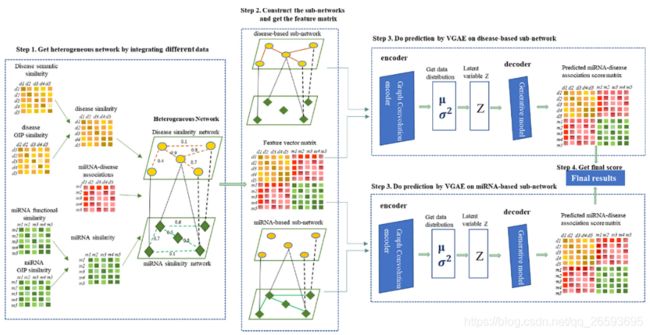
作者先构建了Heterogeneous network的网络，将两个子网络的邻接矩阵对角排列，上三角和下三角反应的就是两个子网络之间的联系，形成异构网络的邻接关系。接着分别训练了两个VAGE子结构，两个子自编码器，分别mask了miRNA-based和disease-based，最终将两个子结构预测出的关系矩阵进行合并，子矩阵的阈值可以不一样。

思考

   作者的思路还是挺自然的，想通过两个异构子网络的交互，来分别预测出子网络中节点之间的关系，试图挖掘子网络中的节点的潜在关系，这样异构网络的关系可以用来进行约束和辅助推断。虽然文章可解释性较强，但是却缺少了一些创新性，本质上对模型没有进行太大的改进，只是将模型进行了多次拼凑，从生物学角度或许是一个不错的想法。

HGA（Heterogeneous Graph Attention Network Xiao）

  图神经网络作为一种基于深度学习的功能强大的图表示技术，表现出了优越的性能。然而，对于包含不同类型节点和链接的异构图，图神经网络并没有充分考虑到这一点。本片作者的工作解决了如何将异构性和丰富的语义信息给异构图的图神经网络的问题。

Fig6 HAN整体模型框架

Node-level Attention:

在具体任务中，一个节点在meta-path上的邻居节点有不同的重要性。Node-level attention部分学习一个节点基于meta-path的邻居节点的表示作为该节点的embedding。由于graph中包含不同类型的node，所以首先通过转换矩阵将所有节点转换到统一的特征空间，再通过学习每个邻居节点的权重，最后softmax计算出节点的权重系数，这里的系数也是非对称，${\varphi }_i$表示一条meta-path。
$$\begin{gathered} h_i^{{}^{\prime }}=M_{{\varphi }_i}\cdot h_i \\ {e}_{ij}^{\Phi }=at{t}_{node}(h_i^{{}^{\prime }},h_j^{{}^{\prime }};\Phi ) \\ {a}_{ij}^{\Phi }=softma{x}_j(e_{ij}^{\Phi })=\frac{exp(\sigma (a_{\Phi }^T\cdot [h_i^{{}^{\prime }}||h_j^{{}^{\prime }}]))}{{\sum }_{k\in {\mathcal{N}}_i^{\Phi }}exp(\sigma (a_{\Phi }^T\cdot [h_i^{{}^{\prime }}||h_k^{{}^{\prime }}])} \end{gathered}$$

公式(7) Node-level 计算

聚合所有邻居节点的系数，就能得到一条meta-path的embedding，这是node级别的attention聚合：
$$z_i^{\Phi }=\sigma (\sum _{j\in {\mathcal{N}}_i^{\Phi }}{a}_{ij}^{\Phi }\cdot h_j^{{}^{\prime }})（8）$$

由于异构图数据是scale free的，计算后会有很高的方差，论文通过将Node-level Attention延伸到了Multihead Attention来解决这个问题,将多个attention进行concatenate，使得训练更加稳定，至此我们就得到了每个mate-path的embedding。
$$z_i^{\Phi }={\parallel }_{k=1}^K\sigma (\sum _{j\in {\mathcal{N}}_i^{\Phi }}{a}_{ij}^{\Phi }\cdot h_j^{{}^{\prime }})（9）$$

Semantic-level Attention:

接下来进行语义级别的Attention聚合，和node level类似，根据meta-path将多种语义信息融合到一起。

Fig7 节点级和语义级聚合过程

作者首先使用一层的MLP将Semantic embedding进行非线性转换。通过学习Semantic-level Attention vector $q$ 来衡量多条Semantic embedding 间的相似性
$$w_{{\Phi }_i}=\frac{1}{|\mathcal{V}|}\sum _{i\in \mathcal{V}}{q}^T\cdot tanh(W\cdot z_i^{\Phi }+b)(10)$$
之后同样，经过Softmax函数，得到语义权重，再将每个path聚合，获得的语义层的embedding。
$$\begin{gathered} {\beta }_{{\Phi }_i}=\frac{exp(w_{{\Phi }_i})}{{\sum }_{i=1}^{P}exp(w_{{\Phi }_i})}(11) \\ Z=\sum _{i=1}^P{\beta }_{{\Phi }_i}\cdot Z_{{\Phi }_i}(12) \end{gathered}$$
最后我们采用半监督学习，通过最小化预测节点的交叉熵来训练模型。
$$L=-\sum _{l\in {\mathcal{Y}}_{\mathcal{L}}}{Y}^{l}ln(C\cdot Z^l)(13)$$
其中C是分类器参数，${\mathcal{Y}}_{\mathcal{L}}$是标签节点集合，$Y^l$和$Z^l$分别是标签和节点embedding。

思考

  可以看到作者主要做了两个方面的信息融合，一个是mate-path上多个异构节点的信息注入，另一个是多个mate-path的信息注入，它能解决异构图中多种Node、Relation，以及Semantic融合的问题。其次该模型能够并行计算，整个模型的Attention是共享的，具有很好的可解释性。

时序图

  在图结构的数据中，还有一类特殊的数据形式，那就是具有时序性的图结构数据。节点的数据或者特征具有时序性，由这些节点构成的图就可能随时间而变化的，又或者这些节点在embedding时需要考虑时空上的关系。时序图在我们日常生活中非常常见，比如video就是一组一帧帧随时间变化的图片，如果从每一帧图片上构建图的拓扑结构，那么就形成了具有图结构的时间序列数据。如何有效把空间上的拓扑信息，与时空上的时序信息进行嵌入融合，是我们需要考虑和研究的问题。

ST-GCN（Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition）

  这是一篇将GCN运用到动作识别上的文中，以往关于图的运用的文章也特别多，但是这篇文章充分考虑了时序上的特征融合，对于识别准确率有显著的提升效果。（作者的脑洞还是挺大的，也算是这一方向的开山之作）

Fig8 人体骨骼时空上排列

首先在空间上定义人体骨骼的拓朴结构，由18个node组成，每个node通过空间坐标和置信度表示，在一帧帧的图片上形成具有时空性质的拓扑结构。空间上采用常规的图卷积来获取信息，时空上采用1*K的卷积核，通过交替使用GCN与TCN，最后使用平均池化、全连接层对特征进行分类。为了使模型更好的收敛，我们在时间和空间维度下进行了归一化。

Fig9 时空变换 （图片来源知乎）

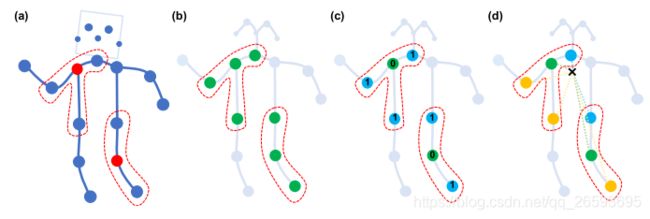
同时为了让模型对运动行为具有更强的表达能力，作者提出了类似GoogleNet 的中inception的思路，结合运动分析研究，定义了三种图卷积核，将原始的图结构划分为三个子图，分别表达 向心运动、离心运动和静止的动作特征 。

Fig10 卷积核区分策略

• 第 1 部分连接了空间位置上比本节点更远离整个骨架重心的邻居节点（黄色节点），包含了离心运动的特征。
• 第 2 部分连接了更为靠近重心的邻居节点（蓝色节点），包含了向心运动的特征。
• 第 3 部分连接了根节点本身（绿色节点），包含了静止的特征
  详细细节，可参考知乎:如何评价ST-GCN动作识别算法

关于时空卷积部分，其实还有很多其他方法可以做，比如LSTM，Attention，GRU等等。另外空间部分，作者还尝试使用了GAT（图注意力机制）来对不同部位的进行加权，这也能够很自然的理解，比较不同类型的行为，身体部位的重要程度就不一样。

思考

  总体来看作者的工作是具有开创性的，从一个新的视角考虑行为识别的任务，同时简洁清晰地表达出了整个模型的训练流程，为后续工作的改进和研究提供了方向。

Hierarchical Video Frame Sequence Representation with Deep Convolutional Graph Network（层次化视频帧序列）

  不同于ST-GCN通过引入时空卷积，来融入时序信息，这篇出自阿里的文章，从另外一个角度来分析和引入时域信息，有趣且新颖，为后续相关工作提供了一种新的视角。

文章主要思想是考虑到视频是一种层次化的数据结构，由事件、场景、镜头、超帧和帧组成。此外，帧之间的关系，镜头之间的关系比序列的顺序结构更为复杂。以如图1所示的烹饪表演为例，包含相同目标的帧不是连续的，并且有不同的时间戳分布。对于这种非线性的结构，作者提出利用图结构去组织视频中帧与帧之间的关系，让不同时间戳上的帧也能建立联系。

Fig12 烹饪节目视频帧序列，相同颜色边框的帧包含相似的场景与目标

通过图卷积方式对相近的帧进行聚合，由帧级别的信息逐渐聚合成镜头、事件和视频级别的嵌入信息，最后对其分类。

Fig13 DCGN 过程

对于每一帧图像的特征提取，作者使用Inception-v3 network在ImageNet数据集上预训练，再对视频的每一帧图片进行特征提取，这样就得到了每个节点的输入特征。节点之间要构建拓扑信息，就需要计算不同节点之间的相关性，作者通过计算帧特征之间的余弦相似度来衡量不同帧之间的相似程度。
$$A(i,j)=\frac{{\sum }_{d=0}^{D-1}(f[i][d]\times f[j][d])}{\sqrt{{\sum }_{d=0}^{D-1}f[i][d{]}^2}\times \sqrt{{\sum }_{d=0}^{D-1}f[i][d{]}^2}}(14)$$
其中，$A$为邻接矩阵，$F\in {\mathbb{R}}^{N\times D}$,$N$是视频帧数也就是节点数量，$D$是特征维度。

通过邻接矩阵对搭建的图结构数据，以消息传递的方式进行图卷积，得到每一个节点更深层的语义信息，然而，在迭代过程中，邻接矩阵A是不变的，图的拓扑是静态的，视频帧序列是一种层次化的动态结构，因此需要逐步将其图的拓扑抽象到更高的层次（可以理解为不同颗粒细度的信息），这里我们主要使用两种池化方法来聚合图。

平均池化:
$$p^l[i][d]=\frac{{\sum }_{k=0}^{K-1}{h}^{l-1}[i\times K+k][d]}{K},d\in [0,D](15)$$
这里$K$是池化尺寸，$p^l[i][d]$是池化后的第$i$行第$d$列。

基于self-attention池化：
$$\begin{gathered} {\alpha }^l[i]=softmax(h^{l-1}[i\times K:(i+1)\times K]W_{att}^l+b^l)(16) \\ {p}_{att[i]}^l=a^l[i]\otimes h^{l-1}[i\times K:(i+1)\times K](17) \end{gathered}$$

通过局部自注意力机制得到[N/K]个归一化的权重系数，加权到每组的K个特征向量上，$\otimes$是克罗内克积(kronecker product)。

节点卷积：

在图卷积中，一般使用全连接层进行关系之间的组合，这里作者用卷积代替了全连接层。
$$c^l[i]=h^{l-1}[i\times K:(i+1)\times K]W^l(18)$$
这里$c^l$是第l层图卷积的节点embedding,$W^l\in {\mathbb{R}}^{K\times D}$是卷积核权重。

Fig14 卷积、池化、局部自注意力计算过程

池化之后的数据，其拓扑结构必然发生改变，所以我们重新计算邻接矩阵，并在下一层图卷积之前跟新邻接矩阵。
至此帧级别的嵌入表达完成，下图描述的是两层图卷积网络，从15个特征向量，聚合层2个节点的过程。

Fig15 特征向量聚合过程

镜头在视频电影中表示一个基本的时间单位，从帧到shoot的分割，采用无监督和非参的学习方式，受到核时态分段(KTS )算法[10]启发，我们将一组帧划分为m段，通过卷积网络提取的特征计算段内的方差，使其方差最小化，便得到了一个最佳的m段划分。
$$\begin{gathered} \underset{m;t_0,...,t_{m-1}}{\min }{J}_{m,n}:=L_{m,n}+Cg(m,n), \\ {L}_{m,n}=\sum _{i=0}^m{v}_{t_{i-1},t_i},g(m,n)=m(log(\frac{n}{m}+1), \\ {v}_{t_{i-1},t_i}=\sum _{t_{i-1}}^{t_i}||f_t-{\mu }_i|{|}^2,u_i=\frac{{\sum }_{t=t_{t_{i-1}}}^{t_i}{f}_t}{t_i-t_{i-1}} \end{gathered}$$

公式19 计算分组

这里$m$是分割shoot的数量，$g(m,n)$是正则项防止分割数量过大，$t_{i-1}$与$t_i$分别表示第i段shoot的起始帧与结束帧索引，$u_i$就是一个shoot的均值,$v$是一个shoot的方差，最后$L_{m,n}$就是要优化的目标。
所以我们将得到了shoot级别的特征聚合：
$$\begin{gathered} p^l[t][d]=\frac{{\sum }_{k=s_t}^{s_{t+1}}f[k][d]}{s_{t+1}-s_t},d\in [0,D](20) \\ {c}^l[t]=f[s_t:s_{t+1}]W^l(21) \end{gathered}$$

这里$s_t$是镜头分段。

分割固定数量的m个镜头后，利用shoot级别的卷积图网络得到shoot特征。然后将深度卷积图网络应用于高层特征的建模。将最后一层特征向量拼接输入MoE混合专家[11]模型，最终得到分类。
读者也可以参考土豆老哥的这篇基于图结构的视频理解

Fig16 shoot分段与聚合过程

思考

  整体来说，文章的想法是非常新颖的，尝试再时间维度上用图的方式建模，将非线性的数据联系到一起。然而笔者认为，文章还是有一些缺点的，后续的工作还有很多点可以挖掘，比如，帧的特征提取需要预训练，并不是完全端到端的学习，其次把通过每一帧图片看成一个节点，构建拓扑关系，太过于复杂，如果是高精度，高采样频率的时序数据节点数量将会非常庞大，不易于学习和训练。
  最后就是文章虽然考虑了不同时间戳上的帧数据的关系，但是通过拓扑图的方式进行表达，自然也瞬时了一部分时序性，不像RNN具有天然是时序性结构。笔者认为这方面可以借鉴transform模型，再图里面加入时序编码的方式，使其注入时间先后的先验知识。

总结

  随着GCN的流行，越来越多的学者从多方面角度来对GCN进行改进与研究，这其中就包括将CV、NLP、推荐系统等多个领域的成果与其相结合。相信未来还会有更多的GNN变体出现，并运用到不同结构特点的数据上。笔者认为，一篇好的文章，就必须要有所创新，或者是在前人工作的基础上对其进行了实质性的优化和改进，而不是简单的拼凑组合，亦或者换一种数据的生搬硬套。其次一篇好文章应该用最简单和通俗的语言，把复杂的计算过程讲解的通俗易懂，当然生动有趣也是文章的加分项了，毕竟一篇有趣且思路清晰的文章，读起来真的让人赏心悦目，直呼妙哉！

  本系列的学习笔记也就先告一段落，后续笔者就要开始做实验了（> <）。之后如果有遇到好的文章，会单独写一篇博客，从公式推导到源码解读与结果复现，完完整整记录下来。

参考文献

[1] https://blog.csdn.net/qq_26593695/article/details/109538241

[2] M. Schlichtkrull, T. N. Kipf, P. Bloem, R. van den Berg, I. Titov, and M. Welling, “Modeling Relational Data with Graph Convolutional Networks,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), vol. 10843 LNCS, no. 1, pp. 593–607, 2018.

[3] S. S. F. Begum, A. Rajesh, and M. Vinnarasi, “Meta path based Top-K Similarity join in heterogeneous information networks,” J. Chem. Pharm. Sci., vol. 9, no. 4, pp. 2217–2220, 2016.

[4] X. Wang et al., “Heterogeneous graph attention network,” Web Conf. 2019 - Proc. World Wide Web Conf. WWW 2019, no. May, pp. 2022–2032, 2019.

[5] S. Yan, Y. Xiong, and D. Lin, “Spatial temporal graph convolutional networks for skeleton-based action recognition,” 32nd AAAI Conf. Artif. Intell. AAAI 2018, pp. 7444–7452, 2018.

[6] Y. Ding, L. P. Tian, X. Lei, B. Liao, and F. X. Wu, “Variational graph auto-encoders for miRNA-disease association prediction,” Methods, no. August, pp. 0–1, 2020.

[7] T. N. Kipf and M. Welling, “Variational Graph Auto-Encoders,” no. 2, pp. 1–3, 2016.

[8] F. Mao, X. Wu, H. Xue, and R. Zhang, “Hierarchical video frame sequence representation with deep convolutional graph network,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), vol. 11132 LNCS, pp. 262–270, 2019.

[9] https://zhuanlan.zhihu.com/p/34998569

[10] Potapov, D., Douze, M., Harchaoui, Z., Schmid, C.: Category-specific video sum- marization. In: European conference on computer vision, Springer (2014) 540–555

[11] Jordan, M.I., Jacobs, R.A.: Hierarchical mixtures of experts and the em algorithm. Neural computation 6(2) (1994) 181–214