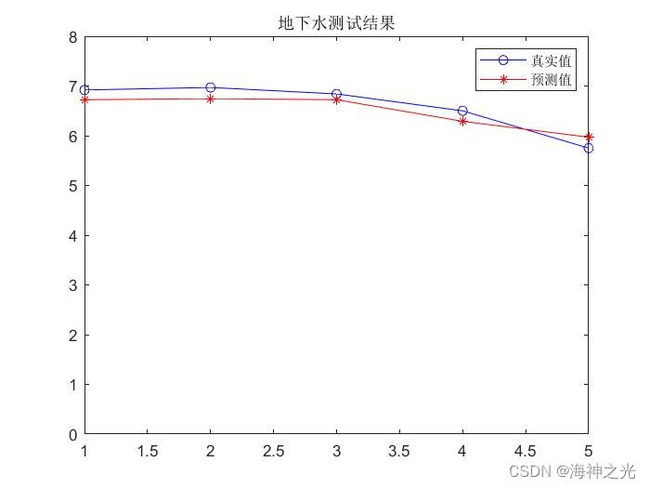
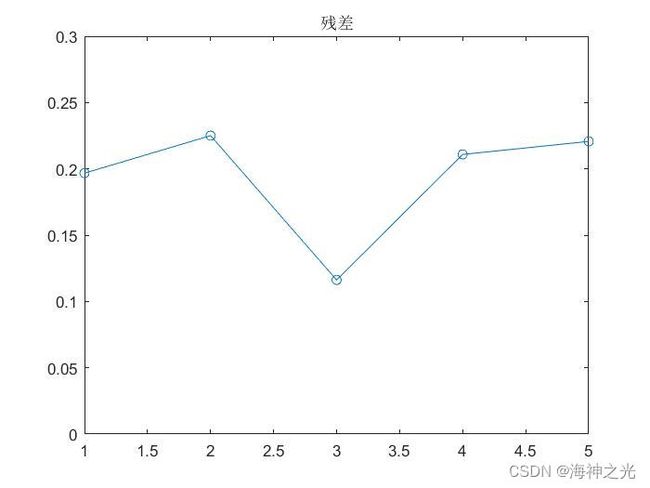
【水位预测】基于matlab径向基神经网络地下水位预测【含Matlab源码 1939期】
一、获取代码方式
获取代码方式1:
完整代码已上传我的资源:【水位预测】基于matlab径向基神经网络地下水位预测【含Matlab源码 1939期】
获取代码方式2:
通过订阅紫极神光博客付费专栏,凭支付凭证,私信博主,可获得此代码。
备注:
订阅紫极神光博客付费专栏,可免费获得1份代码(有效期为订阅日起,三天内有效);
二、RBF神经网络简介
1 RBF神经网络
1.1 RBF神经网络结构
在地下水位预测研究方面, 国内外先后使用多种神经网络模型 (如BP网络、小波网络、L-M网络等) , 通过不同的神经网络进行建模, 对地下水位进行预测。在这些预测的模型中, BP神经网络的使用率最高, 但BP网络在预测高精度地下水水位时, 会出现振荡、收敛速度慢、容易陷入极小值等问题。因此, 在对地下水位预测研究中, 可以考虑使用RBF神经网络进行预测。
1988年Broomhead和Lowe首先将RBF应用于神经网络设计, 从而构成RBF神经网络。其是一种局部逼近的神经网络, RBF神经网络具有良好的泛化能力, 网络结构简单, 避免了不必要的、冗长的计算[3]。关于RBF神经网络的研究表明RBF神经网络能在一个紧凑集合任意精度下, 逼近任何非线性函数。
RBF神经网络属于前向神经网络类型。RBF神经网络的结构与多层前向网络类似, 具有输入层、隐含层和输出层。输入层由信号源节点组成, 隐含层的单元数由所描述的问题的需要而定, 隐含层中神经元的变换函数即径向基函数是对中心点径向对称且衰减的非负非线性函数, 该函数是局部相应函数, 而以前的前向网络变换函数都是全局响应的函数, 输出层是对输入模式做出响应见图1。
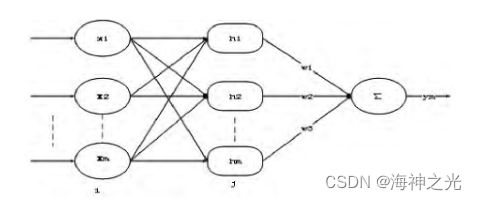
图1 RBF神经网络结构
RBF神经网络的权值为:

RBF神经网络输出位为:
![]()
1.2 RBF神经网络模型的设计、数据处理及训练方式和检验
1.2.1 RBF神经网络模型的设计
以Matlab2016b为平台, 使用RBF神经网络最常用的newrb函数, 创建网络语句net=newrb (input_train, output_train, er, spread, N) 。newrb函数创建网络时, 一开始是没有RBF神经元的, 其首先从输入数据最大误差的样本着手, 增加一个RBF神经元得到相应的输出, 然后重新设计网络线性层逐步减小误差, 反过来又重复根据下一个最大误差的样本, 再增加一个神经元, 循环往复使误差减小, 直至误差达到规定的误差性能或神经元数量达到上限时, 整个创建网络模型才算结束。
1.2.2 数据处理
数据归一化及反归一化处理, 数据归一化方法是神经网络预测前对数据常做的一种处理方法。其作用是把所有的数据都转化为[0, 1]之间的数, 去掉数据间量纲的影响, 简单的讲就是由于数据单位不一致, 所以需要将不同的数据进行格式化, 使之在指定的范围内。以此避免了因为输入输出数据量级差别较大而造成网络预测误差较大。

1.2.3训练方式及检验
RBF神经网络有两种训练方式:聚类方式 (自监督训练方式) +监督训练方式。RBF神经网络第一阶段为非监督学习, 其是从数据中选取记忆样本。第二阶段为监督学习, 此阶段为BP神经网络的学习方式, 是训练记忆样本与样本输出的联系。所以, BP神经网络能实现的功能在RBF神经网络上也能实现, 但是反之未必能实现。将检验样本的预测值与实际值进行对比, 计算其相对误差和平均相对误差。预测精度一般根据平均相对误差MRE进行分级, 分级原则见表1。
三、部分源代码
% rbf_underwater.m
%% 清理工作空间
clear,clc
close all
%% 定义输入数据
% 输入
x = [ 1.5, 1.8, 4.0, 13.0, 5.0, 9.0, 10.0, 9.0, 7.0, 9.5, 5.5, 12.0,...
1.5, 3.0, 7.0, 19.0, 4.5, 8.0, 57.0, 35.0, 39.0, 23.0, 11.0, 4.5;
-10.0, -10.0, -2.0, 10.0, 17.0, 22.0, 23.0, 21.0, 15.0, 8.5, 0, -8.5,...
-11.0, -7.0, 0, 10.0, 18.0, 21.5, 22.0, 19.0, 13.0, 6.0, 1.0, -2.0;
1.2, 2.0, 2.5, 5.0, 9.0, 10.0, 8.0, 6.0, 5.0, 5.0, 6.2, 4.5,...
2.0, 2.5, 3.0, 7.0, 10.0, 11.0, 5.5, 5.0, 5.0, 3.0, 2.0, 1.0;
1.0, 1.0, 6.0, 30.0, 18.0, 13.0, 29.0, 74.0, 21.0, 15.0, 14.0, 11.0,...
1.0, 2.0, 4.0, 0, 19.0, 81.0, 186.0, 114.0, 60.0, 35.0, 4.0, 6.0;
1.2, 0.8, 2.4, 4.4, 6.3, 6.6, 5.6, 4.6, 2.3, 3.5, 2.4, 0.8,...
1.3, 1.3, 4.1, 3.2, 6.5, 7.7, 5.5, 4.6, 3.6, 2.6, 1.7, 1.0
];
y = [6.92, 6.97, 6.84, 6.5, 5.75, 5.54, 5.63, 5.62, 5.96, 6.3, 6.8, 6.9,...
6.7, 6.77, 6.67, 6.33, 5.82, 5.58, 5.48, 5.38, 5.51, 5.84, 6.32, 6.56];
%% 划分训练数据与测试数据
% 测试输入向量
testx = x(:,1:5);
% 测试样本对应的输出
testy = y(1:5);
%% 对训练样本做插值
% 训练样本的个数
N = size(trainx, 2);
X = [trainx; trainy];
% 网格
[xx0, yy0] = meshgrid(1:N, 1:6);
[xx1,yy1] = meshgrid(linspace(1,N,100), 1:6);
% 使用interp2函数做二维三次插值
XX = interp2(xx0, yy0, X, xx1, yy1, 'cubic');
% 形状复原
trainx = XX(1:5, :);
trainy = XX(6, :);
% 神经元个数
N = 101;
net = newrb(trainx, trainy, er, spread, N);
%% 测试
yy = net(testx);
%% 计算、显示相对误差
e = (testy - yy)./testy;
fprintf('相对误差: \n ');
fprintf('%f ', e);
fprintf('\n\n');
% 平均相对误差
m = mean( abs(e) );
fprintf('平均相对误差: \n %f\n', m);
四、运行结果
五、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 王晓伟,赵斌,戈天剑,陈金.基于RBF神经网络地下水位预测[J].农业科技与信息. 2018,(04)
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除