第十三届蓝桥杯python B组个人题解

2022第十三届蓝桥杯python B组个人题解

**此题解仅代表个人意见，不是标准答案，欢迎商量讨论

比赛代码没办法用U盘拷贝，所以纯属赛后重新打，思路可能与比赛那种高压情况下不一样。

A：排列字母

代码：

s = "WHERETHEREISAWILLTHEREISAWAY"
s = list(s)
s.sort()
for i in range(0, len(s)):
    print(s[i], end = "")
print()

结果：

AAAEEEEEEHHHIIILLRRRSSTTWWWY

B、寻找整数

比赛时，猜了个

2022040920220409

比赛时经过验证这个数符合题目要求，但不一定是最小的一个。

个人经验：这种数字大到10的17次方的题目，一般就不当人，不让人正常算出来的。而且，蓝桥杯特别喜欢出这种和比赛时间相关的题目，比赛时可大胆猜测，hh

C、纸张尺寸

代码

a, b = 1189, 841
s = list(input())
n = int(s[1])
for i in range(0, n) :
    a //= 2
    if a < b : a, b = b, a
print(a)
print(b)

D、数位排序

n = int(input())
m = int(input())
tmp = []
for i in range(1, n + 1) :
    t = i
    res = 0
    while t :
        res += (t % 10)
        t //= 10
    tmp.append([res, i])
tmp.sort(key = lambda x : (x[0], x[1]))
print(tmp[m - 1][1])

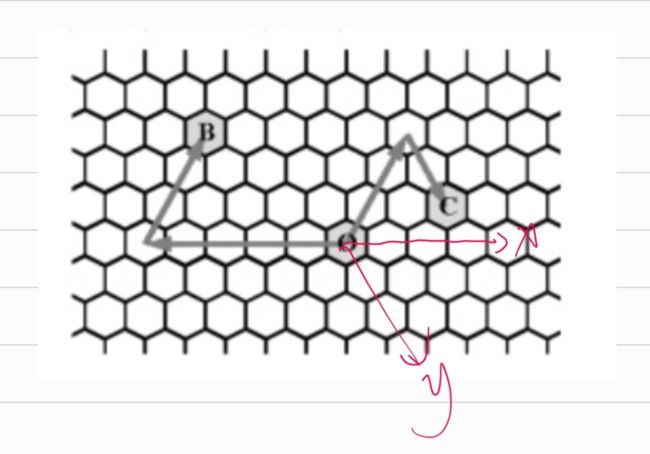
E、蜂巢

首先，先确定x, y 两轴的方向

然后就寄啦，因为要考虑多个方向，希望能拿到一个数据分吧。哭

然后再确定点在这个坐标轴的位置

代码：

nums = list(map(int, input().split()))

res = [[0, 0], [0, 0]] # x1, y1 | x2, y2
for i in range(0, 2) :
    if nums[0] == 0 :
        res[i][0] = -(nums[1] - nums[2])
        res[i][1] = -nums[2]
    elif nums[0] == 1 :
        res[i][0] = nums[2]
        res[i][1] = -nums[1]
    elif nums[0] == 2 :
        res[i][0] = nums[1]
        res[i][1] = -(nums[1] - nums[2])
    elif nums[0] == 3 :
        res[i][0] = nums[1] - nums[2]
        res[i][1] = nums[2]
    elif nums[0] == 4 :
        res[i][0] = -nums[2]
        res[i][1] = nums[1]
    else :
        res[i][0] = -nums[1]
        res[i][1] = nums[1] - nums[2]
    # 其实，两两对应，可以优化，但是，懒
    # 换下，简化计算
    nums[0], nums[1], nums[2] = nums[3], nums[4], nums[5]
print(abs(res[0][0] - res[1][0]) + abs(res[0][1] - res[1][1]))

F、消除游戏

代码：

s = list(input())
for _ in range(0, 2 ** 64) :
    if len(s) == 0 : break
    mark = [0 for i in range(len(s) + 1)]
    f = 1
    for i in range(1, len(s) - 1) :
        if s[i] == s[i - 1] and s[i] != s[i + 1] :
            f = 0
            mark[i] = mark[i + 1] = 1
        if s[i] == s[i + 1] and s[i] != s[i - 1] :
            f = 0
            mark[i] = mark[i - 1] = 1
    t = 0
    if f : break
    for i in range(0, len(s)) :
        if mark[i] : continue
        s[t] = s[i]
        t += 1
    s = s[:t]

if len(s) == 0 : print('EMPTY')
else :
    for i in range(0, len(s) - 1) :
        print(s[i], end = "")
    print(s[len(s) - 1])

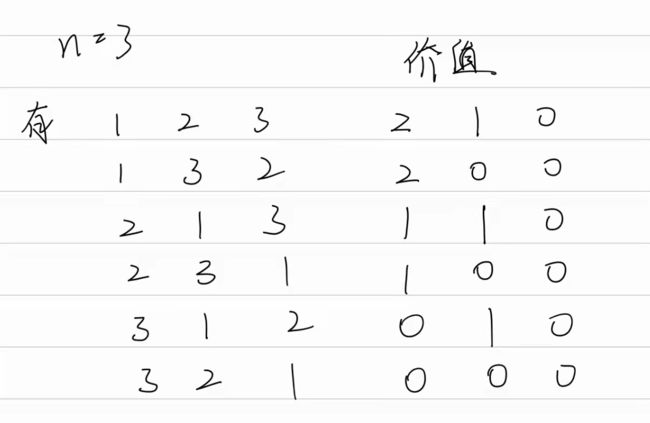
G、全排列的价值

找规律

从这里，应该可以看出一点点规律，再找n = 4

后面我懒得写了，但是也可以看出规律

由此就可以写代码了

朴素版

n = int(input())
mod = 998244353
t = 1 # 阶乘
s = 0 # 和
for i in range(1, n + 1) :
    t *= i
    s += i
res = 0
for i in range(1, n + 1) :
    s -= (n - i + 1)
    res += (s * t // (n - i + 1))
print(res % mod)

但这显然是过不了大量样例的，因为阶乘太大

所以需要用到快速幂求逆元的方法进行优化

n = int(input())
mod = 998244353
t = 1 # 阶乘
s = 0 # 和

def ksm(a, b, p) :
    res = 1
    while b :
        if b & 1 :
            res = res * a % p
            b -= 1
        else :
            a = a * a % p
            b //= 2
    return res

for i in range(1, n + 1) :
    t *= i
    t %= mod
    s += i
res = 0
for i in range(1, n + 1) :
    s -= (n - i + 1)
    res += (s * t * ksm(n - i + 1, mod - 2, mod))
    res %= mod
print(res % mod)

H、技能升级

一开始以为是组合背包，后来觉得是贪心。

from heapq import *
n, m = map(int, input().split())
heap = []
for i in range(n) :
    a, b = map(int, input().split())
    heappush(heap, [-a, b]) # python自带的heapq是小根堆，手动改大根(doge)
res = 0
for i in range(m) :
    if heap == [] : break # 比赛时忘记了，心态有点小炸
    a, b = heappop(heap)
    a = -a
    res += a
    a -= b
    if a > 0 :heappush(heap, [-a, b])
print(res)

I、最长不下降子序列

这题目测动态规划

N, K = map(int, input().split())
nums = list(map(int, input().split()))
dp1 = [1 for _ in range(N)]  # 从前往后
dp2 = [1 for _ in range(N)]  # 从后往前
tmp1 = [nums[0]]
tmp2 = [nums[-1]]
for i in range(1, N) :
    if nums[i] >= tmp1[-1] :
        tmp1.append(nums[i])
        dp1[i] = len(tmp1)
    else :
        for j in range(len(tmp1) - 2, -1, -1) :
            if nums[i] >= tmp1[j] :
                tmp1[j + 1] = nums[i]
                dp1[i] = j + 2
                break
    if nums[N - i - 1] < tmp2[-1] :
        tmp2.append(nums[N - i - 1])
        dp2[N - i - 1] = len(tmp2)
    else :
        for j in range(len(tmp2) - 2, -1, -1) :
            if nums[N - i - 1] < tmp2[j] :
                tmp2[j + 1] = nums[N - i - 1]
                dp2[N - i - 1] = j + 2
                break
res = 0

for k in range(0, K + 1) :
    for i in range(0, N - k - 1) :
        res = max(res, dp1[i] + dp2[i + k] + k - 1)
print(res)

J、最优清零方案

代码

N, k = map(int, input().split())
nums = list(map(int, input().split()))
res = 0
while sum(nums) > 0 :
    for i in range(0, N - k + 1) :
        if nums[i] == 0 : continue
        f, Min = 1, nums[i]
        for j in range(i + 1, i + k) :
            Min = min(Min, nums[j])
            if nums[j] == 0:
                f = 0
                break
        if f :
            res += Min
            for j in range(i, i + k):
                nums[j] -= Min
        else :
            res += nums[i]
            nums[i] = 0
    for i in range(0, N) :
        if nums[i] > 0 :
            res += nums[i]
            nums[i] = 0
print(res)

        break
    if f :
        res += Min
        for j in range(i, i + k):
            nums[j] -= Min
    else :
        res += nums[i]
        nums[i] = 0
for i in range(0, N) :
    if nums[i] > 0 :
        res += nums[i]
        nums[i] = 0

print(res)