优化|列生成算法及Java调用cplex实现
优化|列生成算法及Java调用cplex实现
- Cutting Stock Problem
- Column Generation Algorithm
- Java调用cplex实现CG算法
Cutting Stock Problem
本文中的课件来自清华大学深圳国际研究生院,物流与交通学部张灿荣教授《高级运筹学》课程。
列生成算法的引入,让我们从一个经典的问题开始,即下料问题(Cutting Stock Problem)。

假设有某家公司售卖3种尺寸分别为3-ft、5-ft和9-ft的产品,3种产品的需求量分别为25、20和15。那么这家公司该如何在满足其需求的前提下,通过切割一条17-ft的木板,最大程度地减少浪费呢。

我们当然可以手动推导一些方案出来,如上图所示就有6种不同的方案。对于以有的方案,我们可以按以下的方式建立模型:

这里可以思考一个问题,模型中每一列的 x i x_i xi在每一行约束中对应系数的物理意义是怎样的?
但是如果候选方案的数量巨大,那么约束的长度会很长,甚至没有办法去罗列出所有的切割方案。
Column Generation Algorithm
为了解决类似CSP的问题,学者们提出了一种解决大规模线性规划的算法:列生成算法。
通常求解线性规划的方法为单纯形法,对于单纯形法来说,有:
x B T = B − 1 b T − B − 1 N x N T x_B^T=B^{-1}b^T-B^{-1}Nx_N^T xBT=B−1bT−B−1NxNT
z = c B B − 1 b T + ( c N − c B B − 1 N ) x N T z=c_BB^{-1}b^T+(c_N-c_BB^{-1}N)x_N^T z=cBB−1bT+(cN−cBB−1N)xNT
在传统的方法下,每一列 N j ∈ N N_j \in N Nj∈N,都会调用 c j − c B B − 1 N c_j-c_BB^{-1}N cj−cBB−1N来选择一列 N j ∗ N_j^* Nj∗,它对应于具有最大负值的非基本变量 x j ∗ x_j^* xj∗。这是一种枚举的方法,如果非基本变量的规模很大,那么计算工作量就会很大。那么该怎样简化这个枚举的过程呢?
从上面的模型可以观察到,每一种切割方案 x i x_i xi在每一行约束中对应系数的物理意义为该方案对应切割3种不同尺寸产品的个数。根据这一点就可以对问题做一个转化,来决策一个列 N j N_j Nj是怎样。它对应一种切割方案 ( a 1 , a 2 , a 3 ) T (a_1,a_2,a_3)^T (a1,a2,a3)T,在本文的例子中,它满足 3 a 1 + 5 a 2 + 9 a 3 ≤ 17 3a_1+5a_2+9a_3\le 17 3a1+5a2+9a3≤17。此外对于一个最小化问题,在选择入基的决策变量时,要选择最优表中对应检验数最小的决策变量,它能够最大化改进原问题的目标函数,那么找出这个决策变量对应的目标函数即为 1 − c B B − 1 ( a 1 , a 2 , a 3 ) T 1-c_BB^{-1}(a_1,a_2,a_3)^T 1−cBB−1(a1,a2,a3)T。那么总结一下,可以通过求解以下的模型来找到一个最优的入基变量:
m i n 1 − c B B − 1 ( a 1 , a 2 , a 3 ) T min 1-c_BB^{-1}(a_1,a_2,a_3)^T min1−cBB−1(a1,a2,a3)T
s . t . 3 a 1 + 5 a 2 + 9 a 3 ≤ 17 s.t.\ \ \ 3a_1+5a_2+9a_3\le 17 s.t. 3a1+5a2+9a3≤17
a 1 , a 2 , a 3 ≥ 0 a n d i n t e g e r a_1,a_2,a_3\ge 0 \ and \ integer a1,a2,a3≥0 and integer
( a 1 , a 2 , a 3 ) T (a_1,a_2,a_3)^T (a1,a2,a3)T即对应一个约束列,因此称为column generation。选择了入基变量之后,再通过 x B T = B − 1 b T − B − 1 N x N T x_B^T=B^{-1}b^T-B^{-1}Nx_N^T xBT=B−1bT−B−1NxNT来选择出基变量。
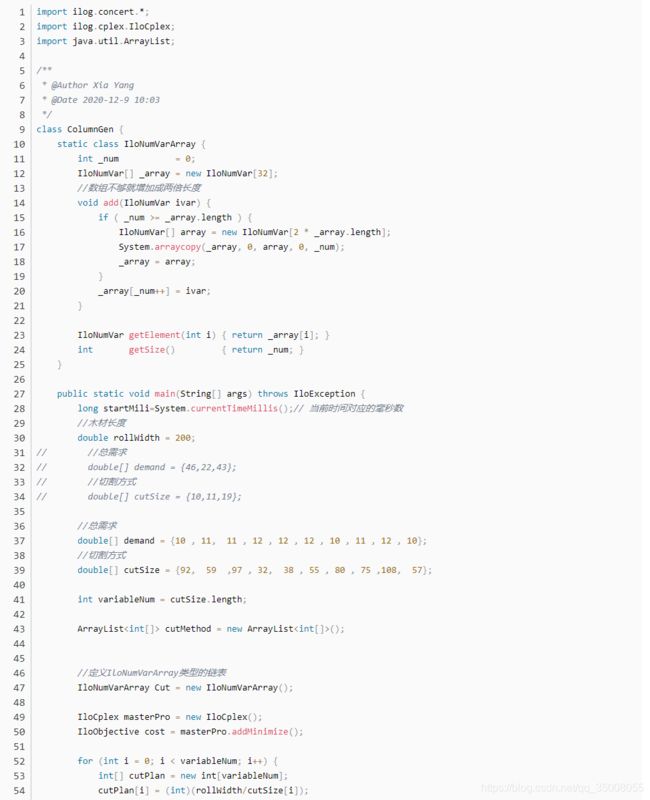
Java调用cplex实现CG算法
感谢大家的阅读,完整project文件请关注公众号并在github获取。下一期会给大家带来CG算法求解Vrptw问题。