AI遮天传 ML-SVM入门
支持向量机(Support Vector Machine,SVM)是Corinna Cortes和Vapnik等于1995年首先提出的,它在解决小样本、非线性及高维模式式识别中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器其学习问题中。
背景信息:
- 支持向量机 (Support Vector Machine,SVM)
- 当前版本的支持向量机大部分是由Vapnik和 他的同事在AT&T贝尔实验室开发的
- 是一个最大间隔分类器(Max Margin Classifier)
- 最开始提出是做分类,后来很快被应用到了回归和时间序列的预测
- 最有效的监督学习方法之一
- 曾被作为文本处理方法的一个强基准模型(strong baseline)
生活引入:
我们生活中经常看到一些影评、物评等等,可以分成三类:
- Pos正面:这款游戏真好玩!
- Neg负面:呸,狗都不玩。
- Neural中性:这是一款像素游戏。
又如我们直到飞机、火车长什么样子,能够在不同的图片将它们分类出来:
再或者我们听一个音乐的音律、节奏,可以辨别出它是何种音乐,如:
- Rock: Michael Jackson “Beat it”
- Hip Hop: Eminem “Lose yourself”
- Blues: Muddy Waters “I can’t be satisfied
对于以上三个例子,我们不难发现,都有一个“中性”的结果,其两侧分别是问题的两种不同的结果,这便是我们今天介绍的 线性向量机 解决问题的思路。
分类方法回顾:
决策树
- 样本的属性非数值
- 目标函数是离散的
贝叶斯学习
- 样本的属性可以是数值或非数值
- 目标函数是连续的(概率)
K-近邻
- 样本是空间(例如欧氏空间)中的点
- 目标函数可以是连续的也可以是离散的
支持向量机 (Support Vector Machine)
- 样本是空间(例如欧氏空间)中的点
- 目标函数可以是连续的也可以是离散的
一、线性支持向量机
给定一个训练样本的集合
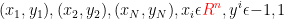
找到一个函数f(x,a) 分类样本,a为参数,使得:
则对于一个测试样本x,我们可以预测它的标签为[f(x,a)]
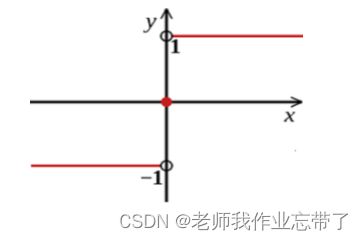
f(x,a) = 0 被称为分类超平面
解释:简单来说就是对于任意+1 正例 的部分,它全部都是大于0的;对于任意-1 负例 的部分,它全部都是小于0的。 电影评价,中评为 分类超平面 ,比中评好的,我们分类为好评,比它差的,我们分类为差评。
线性分类器:
对于一个线性超平面:
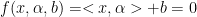
(注:
为向量
的内积即样本特征值和参数的内积,b为截距。)
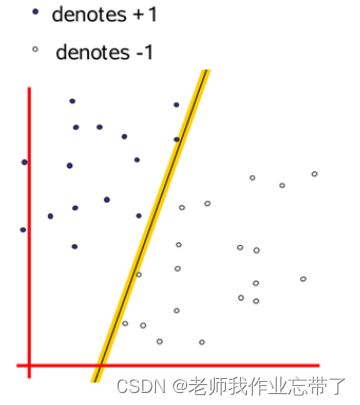
在线性可分的情况下,有无穷多个满足条件的超平面,把结果分成n部分(n=2那分类超平面就是一条线,n=3就是一个面...)
那么哪条线最好呢?
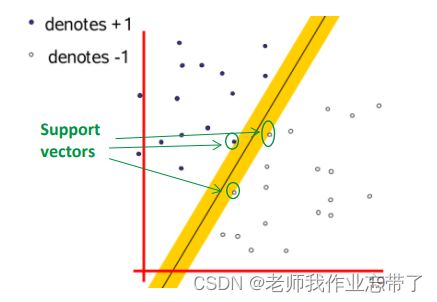
线性分类器的间隔(Margin)
- 在分类分界面两侧分别放置平行于分类超平面的一个超平面 ,移动超平面使其远离分类超平面
- 当他们各自第一次碰到数据点时,他们之间的距离被称为线性分类器的间隔
- Margin (间隔): 分界在碰到数据点之前可以达到的宽度
比如黑线是超平面,两条黄线的边界刚刚触碰到各自的第一个点,上面宽为2,下面宽为3,那间隔就是5.
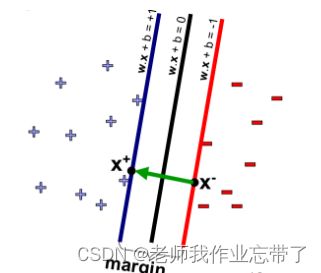
最大间隔线性分类器 (Maximum margin linear classifie)
即具有最大间隔的线形分类器
我们看到这次的黑线(超平面)两端的黄线明显更粗了,所以这条线更好。
那些阻挡间隔继续扩大的数据点,我们叫做支持向量(SV)。
(除了间隔边界上的数据点以外,那些在间隔区域内的、 以及在错误一侧的数据点,也都是SV。后面会讲)
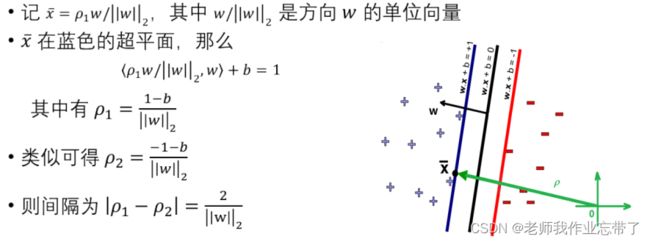
问题形式化
首先,我们需要数据点完美分布在超平面两侧,
引入平行于分类超平面的两个额外超平面:
![]()
间隔即两个新的超平面![]() 之间的距离
之间的距离
如何计算 ![]() ?
?
最优化问题(使间隔最大化):
虽然看起来似乎间隔只与w有关, 但b仍然通过约束w的取值,间接对间隔产生影响。
(因为y为1或-1,![]() 说明都分对了)
说明都分对了)
对偶问题(拉格朗日子乘法)
即经过一系列的转化,我们最终要求的就是在上图红色部分中,在二三行条件下,第一行的最小值。
支持向量
根据KKT条件:![]() (
(![]() >=0)
>=0)
- 当
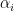 非0 --->
非0 ---> 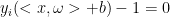 即
即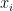 在间隔的边界上(支持向量SV)
在间隔的边界上(支持向量SV) - 大多数
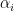 为0,这些
为0,这些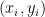 对
对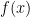 没有什么影响 稀疏解
没有什么影响 稀疏解
线性不可分情况
我们前面提到:首先我们需要数据点完美分布在超平面两侧,这是为了保证训练分类错误率为0.
但是在线性不可分情况下,一定会有错误。
此时找不出一条直线来将他们分隔开来。
我们需要最小化 ![]() 和 训练分类错误!
和 训练分类错误!
其中C>0 是一个用于平衡这二者的常数(前面重要C小一点 后面重要C大一点)
正值常数 C 平衡着 大间隔和小分类错误
Structure risk (结构风险) vs. empirical risk (经验风险)
- 大 C: 更偏向于错误小
- 小 C: 更偏向于间隔大
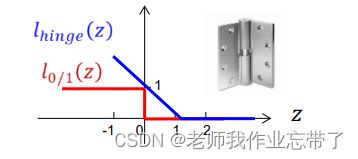
损失函数: 0/1 损失 和 Hinge 损失
回顾正确的预测: ![]()
定义![]()
对每个样本![]() :
:
- 0/1损失:
![]() 非凹凸连续,不容易求解
非凹凸连续,不容易求解
z<0时:
<0时
>0 或
>0时
说明做错了/正例跑到了负例那,负例跑到了正例那。此时loss=1
z>=0时:loss=0
- Hinge损失:
![]()
z<1时,说明点在间隔里面,loss=1-z
z>=1时,loss=0,说明对了
更多损失函数:
形式化损失函数
软间隔(soft margin)
仍然希望找到最大间隔超平面,但此时:
- 我们允许一些训练样本被错分类(
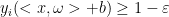 , 不一定全分对了)
, 不一定全分对了) - 我们允许一些训练样本在间隔区域内(是正确的,这次不停下来)
时,数据点在间隔区域的边界上 或 在间隔区域外部正确分类的那一侧
时,数据点在间隔区域内但在正确分类的一侧
时,数据点在分类超平面错误分类的一侧
正值常数 C 平衡着 大间隔和小分类错误
Structure risk (结构风险) vs. empirical risk (经验风险)
- 大 C: 更偏向于错误小
- 小 C: 更偏向于间隔大
对偶问题总结
应用举例: 利用LLC 和 SVM的图像分类
数据集: Caltech101 :9144 张图片、102 类别
预处理:转化为灰度图、放缩图片 e.g. 较长边有120 像素
用LLC (底层特征,Low Level Content) 来提取图像特征
用SVM训练和测试
测试结果
- 训练时每个类别用 15 张图片: 70.16%
- 训练时每个类别用 30 张图片: 73.44%
二、核函数支持向量机 (Kernel SVM)
从输入空间到特征空间 ![]()
样本xi 在输入空间线性不可分,但可能在特征空间中线性可分。
特征空间中的问题
核技巧 (Kernel Tricks)
为了在特征空间中求解对偶问题且找到分类超平面,我们只需知道 ![]() ,(而不是分别的
,(而不是分别的![]() 。)
。)
如果我们已知一个函数 ![]() 它等于
它等于 ![]() 那么我们就没有必要显示地表示这些特征。
那么我们就没有必要显示地表示这些特征。
![]() 称作 核函数(kernel function)
称作 核函数(kernel function)
即只需要知道核函数是什么就好了。
常用核函数
例如:
![]()
即他们地映射结果刚好是相等的所以可以用核函数代表。
三种构造核函数的方法
注:是三种方法;
- 第一种:根据特征函数手动计算核函数
- 第二种:直接选择一个合理的核函数
- 第三种:利用简单核函构造新的核函数
举例: 构造高斯核函数
软件工具
Libsvm :http://www.csie.ntu.edu.tw/~cjlin/libsvm/
Liblinear :http://www.csie.ntu.edu.tw/~cjlin/liblinear/
SVMlight :http://svmlight.joachims.org/
三、SVM的核心概要
线性支持向量机
- 线性可划分问题:最大化间隔
- 线性不可划分问题:最大化间隔且最小化分类错误
- 原始问题不好求,转换为对偶问题。
核函数支持向量机
- 映射到特征空间:
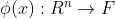
- 核技巧:
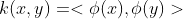
- 3种构造核函数的办法
SVM的优缺点
优点
- 很好的数学基础
- 最大化间隔使得方法的鲁棒性非常高,泛化能力强
- 用线性的方法解决线性不可分问题(两种思路)
- 1.利用soft margin: 最大化间隔且最小化分类错误
- 2.通过从输入空间到特征空间的变换
- 本质上是将在低维空间上线性不可分的问题,通过变换(大多是升维)变成线性可分问 题
- 利用Kernel Trick, 并不需要知道该变换是什么
- 在实际应用中效果往往不错
缺点
- 有多种核函数可用,针对具体问题,哪个核函数最好?
—— 尚未找到理论上可证 明的最优选择