目标检测中目标框回归损失函数(IoU, GIoU, DIoU, CIoU)总结
目标检测中目标框回归损失函数(IoU, GIoU, DIoU, CIoU)总结
1. Smooth L1 Loss
这个是 Faster-RCNN 中的损失函数。具体可以参考深度学习目标检测之 R-CNN 系列:Faster R-CNN 网络详解 中相应介绍。
Smooth L1 Loss 相比 L1 和 L2 的优势可以参考 损失函数:L1 loss, L2 loss, smooth L1 loss。总结其优势就是:
- smooth L1和L1-loss函数的区别在于,L1-loss在0点处导数不唯一,可能影响收敛。smooth L1的解决办法是在0点附近使用平方函数使得它更加平滑
- 相比于L2损失函数,其对离群点、异常值(outlier)不敏感,梯度变化相对更小,训练时不容易跑飞
2. IoU Loss
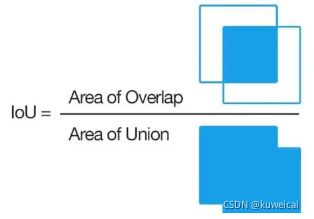
IoU(Intersection over Union) 是旷视在 2016 年于 UnitBox: An Advanced Object Detection Network 中提出的,随后被广泛使用。正如其名交并比,就是两个 BBox 的交集比上并集。
IoU Loss 的数学表达式为 L o s s I o U = − l n ( I o U ) Loss_{IoU} = -ln(IoU) LossIoU=−ln(IoU),实际使用中很多直接简化为 L o s s I o U = 1 − I o U Loss_{IoU} = 1 - IoU LossIoU=1−IoU。
IoU 相比 Smooth L1 Loss 具有如下优势:
- 具有尺度不变性
- IoU Loss,其将 4 个点构成的 box 看成一个整体进行回归
直接看下图更直观。
IoU 的不足:
1)当预测框和目标框不相交时,IoU(A,B)=0时,不能反映A,B距离的远近,此时损失函数不可导,IoU Loss 无法优化两个框不相交的情况。
2)假设预测框和目标框的大小都确定,只要两个框的相交值是确定的,其IoU值是相同时,IoU值不能反映两个框是如何相交的。
3. GIoU Loss
GIoU(Generalized Intersection over Union) 是Hamid Rezatofighi 等2019年于 Generalized Intersection over Union: A Metric and A Loss for Bounding BoxRegression 中提出的一种改进的 IoU Loss。
如下图所示,三种不同相对位置的框拥有相同的IoU=0.33值,但是拥有不同的GIoU=0.33,0.24,-0.1。当框的对齐方向更好一些时GIoU的值会更高一些。
计算过程如下:
GIoU Loss 的表达式为:
L o s s G I o U = 1 − G I o U Loss_{GIoU} = 1 - GIoU LossGIoU=1−GIoU
GIoU 的不足:
如下图,BBox 重合的时候 GIoU 退化为 IoU。
4. DIoU Loss
DIoU(Distance-IoU) 是 Zhaohui Zheng 等 2019 年在 Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression 中提出的。
基于IoU和GIoU存在的问题,作者提出了两个问题:
- 第一:直接最小化预测框与目标框之间的归一化距离是否可行,以达到更快的收敛速度。
- 第二:如何使回归在与目标框有重叠甚至包含时更准确、更快。
好的目标框回归损失应该考虑三个重要的几何因素:重叠面积,中心点距离,长宽比。基于问题一,作者提出了DIoU Loss,相对于GIoU Loss收敛速度更快,该Loss考虑了重叠面积和中心点距离,但没有考虑到长宽比;针对问题二,作者提出了CIoU Loss,其收敛的精度更高,以上三个因素都考虑到了。
通常基于IoU-based的loss可以定义为 L = 1 − I o U + R ( B , B g t ) L = 1 - IoU + R(B, B^{gt}) L=1−IoU+R(B,Bgt),其中 R ( B , B g t ) R(B, B^{gt}) R(B,Bgt) 定义为预测框 B B B和目标框 B g t B^{gt} Bgt 的惩罚项。
DIoU中的惩罚项表示为 R D I o U = ρ 2 ( b , b g t ) c 2 R_{DIoU} = \frac{\rho^{2}(b, b^{gt})}{c^2} RDIoU=c2ρ2(b,bgt) ,其中 b b b 和 b g t b^{gt} bgt 分别表示 B B B 和 B g t B^{gt} Bgt 的中心点, ρ \rho ρ 表示欧式距离, c c c 表示 B B B 和 B g t B^{gt} Bgt 的最小外界矩形的对角线距离,如下图所示。可以将 DIoU 替换 IoU 用于 NMS 算法当中,也即论文提出的 DIoU-NMS,实验结果表明有一定的提升。
DIoU Loss function 定义为: L D I o U = 1 − I o U + ρ 2 ( b , b g t ) c 2 L_{DIoU} = 1 - IoU + \frac{\rho^{2}(b, b^{gt})}{c^2} LDIoU=1−IoU+c2ρ2(b,bgt)
DIoU的性质:
- 尺度不变性
- 当两个框完全重合时, L I o U = L G I o U = L D I o U = 0 L_{IoU} = L_{GIoU} = L_{DIoU} = 0 LIoU=LGIoU=LDIoU=0 ,当2个框不相交时 L G I o U = L D I o U → 2 L_{GIoU} = L_{DIoU} \rightarrow 2 LGIoU=LDIoU→2
- DIoU Loss 可以直接优化 2 个框直接的距离,比 GIoU Loss 收敛速度更快
- 对于目标框包裹预测框的这种情况,DIoU Loss 可以收敛的很快,而 GIoU Loss 此时退化为 IoU Loss 收敛速度较慢
5. CIoU Loss
DIoU 那拨人在 2020 年又整出了个 CIOU( Complete-IoU)。论文见Enhancing Geometric Factors in Model Learningand Inference for Object Detection and InstanceSegmentation。套路和 DIoU 差不多。
CIoU Loss 的表达式如下:
L D I o U = 1 − I o U + ρ 2 ( b , b g t ) c 2 + α υ L_{DIoU} = 1 - IoU + \frac{\rho^{2}(b, b^{gt})}{c^2} + \alpha\upsilon LDIoU=1−IoU+c2ρ2(b,bgt)+αυ
CIoU 的惩罚项是在 DIoU 的惩罚项基础上加了一个影响因子 α υ \alpha\upsilon αυ ,这个因子把预测框长宽比拟合目标框的长宽比考虑进去。其中 α \alpha α 是用于做 trade-off 的参数, α = υ ( 1 − I o U ) + υ \alpha = \frac{\upsilon}{(1 - IoU) + \upsilon} α=(1−IoU)+υυ, υ \upsilon υ 是用来衡量长宽比一致性的参数,定义为 υ = 4 π 2 ( a t c t a n w g t h g t − a r c t a n w h ) \upsilon = \frac{4}{\pi^{2}}(atctan{\frac{w^{gt}}{h^{gt}}} - arctan{\frac{w}{h}}) υ=π24(atctanhgtwgt−arctanhw)。
参考
- 目标检测回归损失函数简介:SmoothL1/IoU/GIoU/DIoU/CIoU Loss