【计算机视觉实战 2 】、特征匹配之Harris角点

---

前言

图像匹配：

特征点匹配，是图像拼接、三维重建、相机标定等应用的关键步骤

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、特征匹配的基本流程是什么？

1.流程

1、根据特定准测，提取图像中的特征点
2、提取特征点周围的图像块，构造特征描述符
3、通过特征描述符对比，实现特征匹配

2.对特征点的要求

必须具有不变性，比如
几何不变性：位移、旋转、尺度
光度不变性：光照、曝光

二、角点是什么？

1.角点

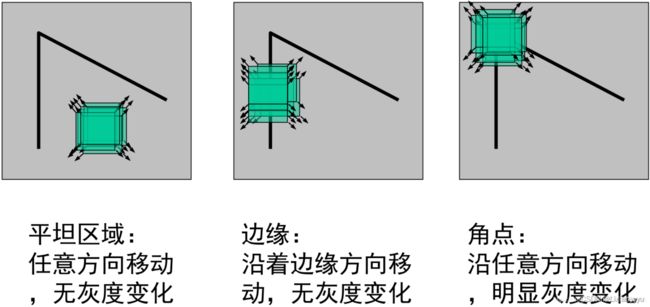
1、局部窗口沿各方向移动，均产生明显变化的点，
2、图像局部曲率突变的点

2.Harris角点检测

基本思想

从图像局部的小窗口观察图像特征，
角点：窗口向任何方向的移动都导致图像灰度的明显变化

数学表达

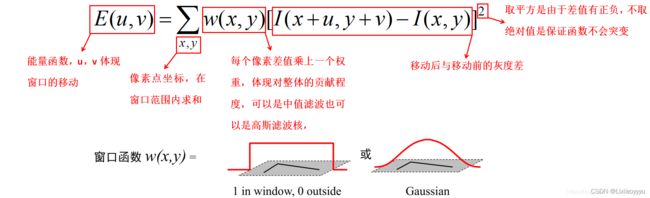
将 函数I(x+u,y+v)在(x，y)处泰勒展开，可得

对M进行特征值分析，并定义R为角点响应函数

3.角点描述子

Harris角点检测紧急能够检测出图像中的兴趣点，没有给出通过比较图像间的兴趣点来寻找匹配角点的方法。
需要在每个点加入描述子信息，

harr角点检测
代码如下（示例）：

from scipy.ndimage import filters
from PIL import Image
from pylab import *
from numpy import *
import matplotlib.pyplot as plt

def compute_harris_response(img, sigma=3):
    # 计算导数
    imx = zeros(img.shape)
    filters.gaussian_filter(img, (sigma, sigma), (0, 1), imx)

    imy = zeros(img.shape)
    filters.gaussian_filter(img, (sigma, sigma), (1, 0), imy)

    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False

    # 可视化原图
    plt.subplot(2, 3, 1)
    plt.title('灰度图')
    plt.axis('off')
    plt.imshow(img, plt.cm.gray)

    # 可视化x方向导数图像
    plt.subplot(2, 3, 2)
    plt.title('x方向导数')
    plt.axis('off')
    plt.imshow(imx, plt.cm.gray)

    # 可视化y方向导数图像
    plt.subplot(2, 3, 3)
    plt.title('y方向导数')
    plt.axis('off')
    plt.imshow(imy, plt.cm.gray)

    plt.subplot(2, 3, 4)
    plt.title('x方向二阶导数')
    plt.axis('off')
    plt.imshow(imx * imx, plt.cm.gray)

    plt.subplot(2, 3, 5)
    plt.title('x/y方向二阶导数')
    plt.axis('off')
    plt.imshow(imx * imy, plt.cm.gray)

    plt.subplot(2, 3, 6)
    plt.title('y方向二阶导数')
    plt.axis('off')
    plt.imshow(imy * imy, plt.cm.gray)
    plt.show()

    # 计算Harris矩阵的分量
    Wxx = filters.gaussian_filter(imx * imx, sigma)
    Wxy = filters.gaussian_filter(imx * imy, sigma)
    Wyy = filters.gaussian_filter(imy * imy, sigma)

    # 计算特征值和迹

    # 矩阵特征值的积等于行列式的值
    Wdet = Wxx * Wyy - Wxy ** 2

    # 主对角线上元素的和称为矩阵的迹，也是特征值的和
    Wtr = Wxx + Wyy
    return Wdet / Wtr

# 从一幅Harris响应图像中返回角点。min_dist为分割角点和图像边界的最少像素数目
def get_harris_points(harrisim, min_dist=10, threshold=0.1):
    # 寻找高于阈值的候选角点
    corner_threshold = harrisim.max() * threshold
    # print(corner_threshold)

    harrisim_t = (harrisim > corner_threshold) * 1
    plt.imshow(harrisim_t, plt.cm.gray)

    # 得到候选点的坐标(取出是角点的坐标)
    coords = array(harrisim_t.nonzero()).T
    # print(coords.shape)

    # 以及它们的Harris响应值
    candidate_values = [harrisim[c[0], c[1]] for c in coords]

    # 对候选点按照Harris响应值进行排序
    index = argsort(candidate_values)

    # 将可行点的位置保存到数组中
    allowed_location = zeros(harrisim.shape)
    # 相当于把外面一圈有响应值的点先舍去（匹配主体在中心）
    allowed_location[min_dist:-min_dist, min_dist:-min_dist] = 1

    # 按照min_distance原则，选择最佳的Harris角点
    filtered_coords = []
    for i in index:
        if allowed_location[coords[i, 0], coords[i, 1]] == 1:
            filtered_coords.append(coords[i])
            allowed_location[(coords[i, 0] - min_dist):(coords[i, 0] + min_dist),
            (coords[i, 1] - min_dist):(coords[i, 1] + min_dist)] = 0

    return filtered_coords


# 绘制图像中检测到的角点
def plot_harris_point(image, filtered_coords):
    figure()
    gray()
    imshow(image)
    plot([p[1] for p in filtered_coords], [p[0] for p in filtered_coords], '*')
    axis('off')
    show()


if "__main__" == __name__:
    # 打开灰度图convert('L')
    img = array(Image.open("IMG_9687.JPG").convert('L'))

    harrisim = compute_harris_response(img)
    filtered_coords = get_harris_points(harrisim, 6)
    plot_harris_point(img, filtered_coords)

结果，右侧为使用阈值0.1检测出的角点

4.特征匹配

分析，对同一幅图片进行特征匹配，效果还是很好的，连接线主要是平行的
但是当从不同角度对尚大楼进行拍摄，就会有很多错误匹配。
图片尺寸均改为500*500

# 获得角点的特征描述（划分以角点为中心的5*5区域）
def get_descriptors(image, filtered_coords, wid=5):
    desc = []
    for coords in filtered_coords:
        patch = image[coords[0] - wid:coords[0] + wid + 1, coords[1] - wid:coords[1] + wid + 1].flatten()
        desc.append(patch)
    return desc


# 归一化互相关获得得分
def match(desc1, desc2, threshold=0.5):
    n = len(desc1[0])
    d = -ones((len(desc1), len(desc2)))
    for i in range(len(desc1)):
        for j in range(len(desc2)):
            d1 = (desc1[i] - mean(desc1[i])) / std(desc1[i])
            d2 = (desc2[j] - mean(desc2[j])) / std(desc2[j])
            ncc_value = sum(d1 * d2) / (n - 1)
            if ncc_value > threshold:
                d[i, j] = ncc_value

    ndx = argsort(-d)
    matchscores = ndx[:, 0]
    return matchscores


# 进行两边对称版本的匹配
def match_twosided(desc1, desc2, threshold=0.5):
    matches_12 = match(desc1, desc2, threshold)
    matches_21 = match(desc2, desc1, threshold)

    ndx_12 = where(matches_12 >= 0)[0]

    # 筛去不匹配的点
    for n in ndx_12:
        if matches_21[matches_12[n]] != n:
            matches_12[n] = -1

    return matches_12


def appendimages(img1, img2):
    rows1 = img1.shape[0]
    rows2 = img2.shape[0]

    if rows1 < rows2:
        img1 = concatenate((img1, zeros((rows2 - rows1, img1.shape[1]))), axis=0)
    elif rows1 > rows2:
        img2 = concatenate((img2, zeros((rows1 - rows2, img2.shape[1]))), axis=0)

    return concatenate((img1, img2), axis=1)


def plot_matches(img1, img2, locs1, locs2, matchscores, show_below=False):
    img3 = appendimages(img1, img2)
    if show_below:
        img3 = vstack((img3, img3))

    imshow(img3)

    cols1 = img1.shape[1]
    for i, m in enumerate(matchscores):
        if m > 0:
            plot([locs1[i][1], locs2[m][1] + cols1], [locs1[i][0], locs2[m][0]], 'c')
    axis('off')


if "__main__" == __name__:
    # 打开灰度图convert('L')

    image = Image.open("IMG_9685.JPG").convert('L')
    base_width = 500
    w_percent = base_width / float(image.size[0])
    h_size = int(float(image.size[1]) * float(w_percent))
    image1 = image.resize((base_width, h_size), Image.ANTIALIAS)
    image1.show()

    image2 = Image.open("IMG_96731.JPG").convert('L')
    w_percent = base_width / float(image2.size[0])
    h_size = int(float(image2.size[1]) * float(w_percent))
    image2 = image2.resize((base_width, h_size), Image.ANTIALIAS)
    image2.show()

    img1 = array(image1)
    img2 = array(image2)
    wid = 5
    harrisim = compute_harris_response(img1, 5)
    filtered_coords1 = get_harris_points(harrisim, wid + 1)
    d1 = get_descriptors(img1, filtered_coords1, wid)

    harrisim = compute_harris_response(img2, 5)
    filtered_coords2 = get_harris_points(harrisim, wid + 1)
    d2 = get_descriptors(img2, filtered_coords2, wid)

    print("starting matching")

    matches = match_twosided(d1, d2)

    figure()
    gray()
    plot_matches(img1, img2, filtered_coords1, filtered_coords2, matches)
    show()

5.SIFT算子

1999年David G.lowe教授总结了基于特征不变技术的检测方法，在图像尺度空间基础上没吐出来对图像缩放、旋转保持不变性的图像局部特征描述算子—SIFT（尺度不变特征变化），该算法在2004年完善

可以解决的问题
1、目标的旋转、缩放、平移（RST）
2、图像放射/投影变化（十点viewpoit）
3、弱光照影响
4、部分目标遮挡
5、杂物场景
6、噪声

总结