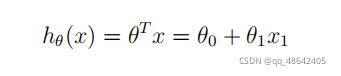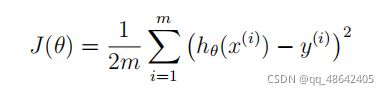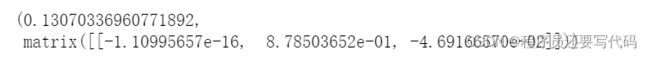吴恩达机器学习作业-Linear Regression（Python实现）

Task1：Linear regression with one variable

首先先引入库

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

用课程所给的数据生成表以及散点图

path='E:\xxx\machine learning\ex1data1.txt'//本地磁盘绝对路径
data=pd.read_csv(path,header=None,names=['population','profit'])
data.head()

其中解释一下比较重要的参数

filepath_or_buffer:可以是本地路径，也可是URL（http, ftp, s3, 和 file）链接等，此参数必加。

sep: 指定分割符，默认是‘,’。

header：指定第几行作为列名(忽略注解的行)，如果没有指定列名，默认header=0;，若指定了列名header=None。

names：指定列名，如果文件中不包含header的行，应该显性表示header=None。

head()函数:打印数据表但由于默认设置只能打印前5行。

打印表：

data.plot(kind='scatter',x='Population',y='Profit',figsize=(12,8))
plt.show()

 plot函数:

kind='参数'表示的含义

1. ‘scatter’ : scatter plot#散点图。需指定X轴Y轴

2. 'line’ : line plot (default)#折线图

3. ‘bar’ : vertical bar plot#条形图。

4. ‘hist’ : histogram#直方图

5. ‘box’ : boxplot#箱型图

6. ‘kde’ : Kernel Density Estimation plot#密度图

7. ‘hexbin’ : hexbin plot#蜂巢图。需指定X轴Y轴

x,y：即定义x，y轴的表示的名称

figsize（a,b）： 设置图形的大小，a为图形的宽， b 为图形的高，单位为英寸

 

构造代价函数

在本部分中，你将使用梯度下降法将线性回归参数θ拟合到我们的数据集上。

下面给出公式

                                       

                                   

def computeCost(X, y, theta):
    inner = np.power(((X * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(X))

 #这个部分计算J(Ѳ)，X是矩阵，power表示乘方，theta.T表示，sum为求和，len表示矩阵长度

在下面几行中，我们向数据添加另一个维度以适应截距项。我们还将初始参数初始化为0，学习速率阿尔法初始化为0.01,迭代次数初始化为1500。

在训练集中添加一列，以便我们可以使用向量化的解决方案来计算代价和梯度。

data.insert(0, 'Ones', 1)

本句意思：在第0列插入1，列名为’Ones’

初始化变量

cols = data.shape[1]  # 列数
X = data.iloc[:,0:cols-1]  # 取前cols-1列，即输入向量
y = data.iloc[:,cols-1:cols] # 取最后一列，即目标向量

data.shape[1]返回的是data的列数，有几列

输出看下是否正确

X.head() 
y.head()

将X,y赋为一个矩阵并初始化theta

X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix([0,0])

运行函数

computeCost(X, y, theta)

 

 梯度下降

 接下来，您将在梯度中实现梯度下降。您需要在每次迭代中向θ提供更新。在编程时，请确保您了解您正在试图优化的内容和正在更新的内容。

先给出公式 

                                         

根据公式写出代码

注意这里用使用举证矢量化相乘，可以同时更新所有的 θ，可以大大提高效率

def gradientDescent(X,y,theta,alpha,epoch):
    temp = np.matrix(np.zeros(theta.shape)) # 初始化一个 θ 临时矩阵(1, 2)
    cost = np.zeros(epoch)# 初始化一个价值矩阵，包含每次epoch的cost
    m = X.shape[0]# 样本数量m
    for i in range(epoch): #迭代求解
        temp =theta - (alpha / m) * (X * theta.T - y).T * X
        theta = temp#更新theta
        cost[i] = computeCost(X, y, theta)#储存cost值
        return theta,cost

初始化参数

alpha = 0.01
epoch = 1000

使用梯度下降算法训练Ѳ并算出代价函数

final_theta, cost = gradientDescent(X, y, theta, alpha, epoch)
computeCost(X, y, final_theta)

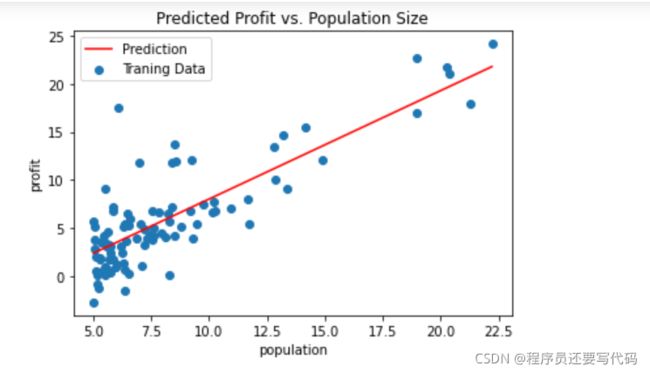
最后来绘制拟合图

x = np.linspace(data.Population.min(), data.Population.max(), 100)  # 横坐标
f = final_theta[0, 0] + (final_theta[0, 1] * x)  # 纵坐标，利润

np.linspace主要用来创建等差数列。

其中这三个参数定义

start:返回样本数据开始点

stop:返回样本数据结束点

num:生成的样本数据量，默认为50

fig, ax = plt.subplots(figsize=(6,4))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)  # 2表示在左上角
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()

下面每条代码一一解释下：

fig, ax = plt.subplots(figsize = (a, b))

其中figsize用来设置图形的大小，a为图形的宽， b为图形的高，单位为英寸。

fig代表绘图窗口(Figure)；ax代表这个绘图窗口上的坐标系(axis)，一般会继续对ax进行操作。

ax.plot(x, f, 'r', label='Prediction')

设置横纵坐标的函数，并设置颜色为红色，在图标上标上'Prediction'标签

ax.scatter(data.Population, data.Profit, label='Traning Data')

定义散点图的横纵坐标，并给出散点图点的'Traning Data'标签名

ax.legend(loc=2)  # 2表示在左上角

定义图例标签位置

ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()

设定x,y轴,以及整个表的名称，最后绘制出来。

效果如下：

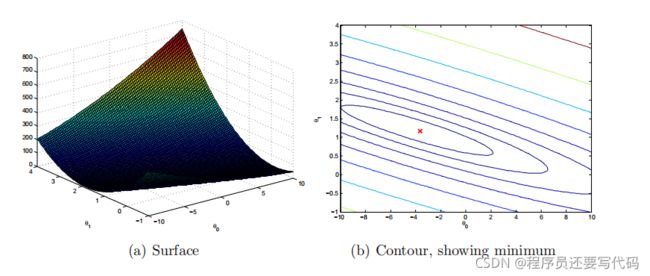
 可视化J（θ）

因为目前并没有找到用python进行实现的方法先贴图以供日后研究。

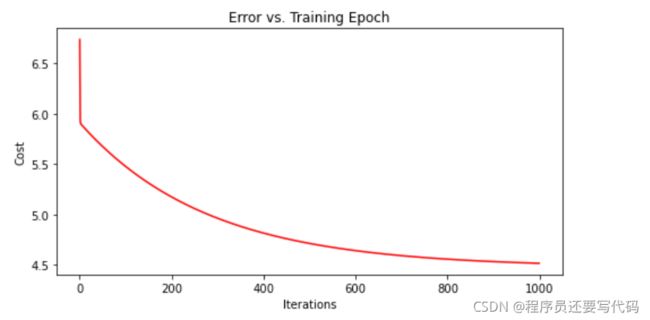
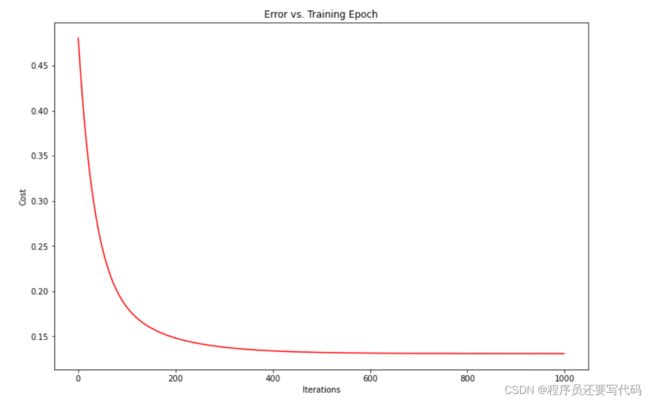
 但我们可以通过python绘制二维图即代加函数与迭代次数的图

fig, ax = plt.subplots(figsize=(8,4))
ax.plot(np.arange(epoch), cost, 'r')  # np.arange()自动返回等差数组
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()

带有多元变量的线性回归

在这一部分中我们有带有两个变量的值（房屋大小和卧室数量）来估计房屋价格。

开始我们照搬上一个例子的处理方法

首先读取数据集

path='E:\xx\xx\ex1data2.txt'
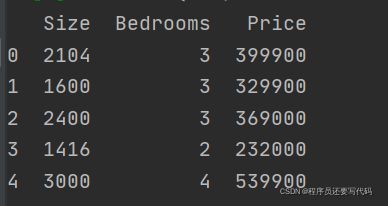
data2 = pd.read_csv(path, names=['Size', 'Bedrooms', 'Price'])
data2.head()

此时由于特征值大小不同需要进行均值归一化

data2 = (data2 - data2.mean()) / data2.std() 
data2.head()

其中mean()函数求每列特征值的平均值，std()求每列特征值的标准差

 

进行求解

data2.insert(0, 'Ones', 1)

cols = data2.shape[1]
X2 = data2.iloc[:,0:cols-1]
y2 = data2.iloc[:,cols-1:cols]

X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)
alpha = 0.01
epoch = 1000
theta2 = np.matrix(np.array([0,0,0]))
g2, cost2 = gradientDescent(X2, y2, theta2, alpha, epoch)
print(computeCost(X2, y2, g2)), g2

 

 由于是多维变量图形不好表示故先略去。

 选择学习速率

首先画出J与迭代次数的关系图

fig, ax = plt.subplots(figsize=(8,4))
ax.plot(np.arange(epoch), cost2, 'r')  # np.arange()自动返回等差数组
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()

正规方程（ Normal Equations）

使用正规方程算法直接得到一个精确的Ѳ解

 

def NormalEquations(X,y):
    theta = np.linalg.inv(X.T*X)*X.T*y
    return theta

其中np.linalg.inv为求矩阵逆的函数

final_theta2=NormalEquations(X2, y2)

计算theta2（大家可以尝试下线性回归和正规方程就出来的theta最后会有一定的误差）

至此作业全部完成，感谢各位观看！