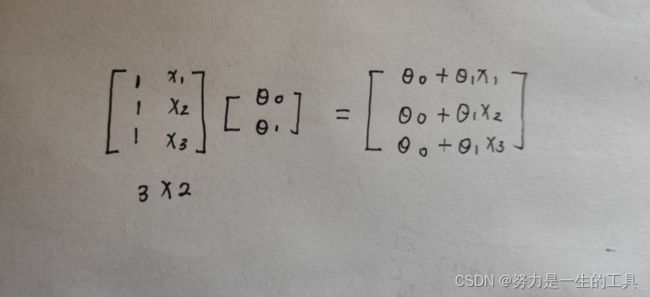吴恩达机器学习 作业一线性回归python实现(注释超级详细)
如有侵权请联系删除
1.引入库
import numpy as np #导入numpy矩阵库
import pandas as pd #类似于excal 用来导入文本文件的
import matplotlib.pyplot as plt #用来画图的2.导入数据
#——————————————————————————下面是数据导入——————————————————————
path ='ex1data1.txt'
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])
#names 相当于给数据加上表头
(1)有的代码中含有data.head() 用于展示前五行
#Return the first `n` rows. n : int, default 5
(2) csv是逗号分隔值文件格式,一般用WORDPAD或记事本(NOTE),EXCEL打开。
pandas.read_csv 是用来读取这个文件
(3)本次是用的是没有表头 我们用names手动加上
| csv文件有表头并且是第一行,那么names和header都无需指定; |
| csv文件有表头、但表头不是第一行,可能从下面几行开始才是真正的表头和数据,这个时候指定header即可; |
| csv文件没有表头,全部是纯数据,那么我们可以通过names手动生成表头; |
| csv文件有表头、但是这个表头你不想用,这个时候同时指定names和header。先用header选出表头和数据,然后再用names将表头替换掉,就等价于将数据读取进来之后再对列名进行rename; |
3.将数据转化为矩阵
#——————————————————————————下面是转化为矩阵——————————————————————
data.insert(0,'Ones',1)#在第0列插入一列,然后这列值全部是1 ones是标题
clos=data.shape[1] #shape[1]意思是取列数 shape[0]取行数 所以clos=3
X=data.iloc[:,0:clos-1]#iloc ,行全部选择 后面参数是选择 0,1列 前开后闭
Y=data.iloc[:,clos-1:clos]#iloc ,行全部选择 后面参数是选择 最后列 前开后闭
X=np.matrix(X) #数据中的 第一 第二列
Y=np.matrix(Y.values) #数据中的第三列 也就是房价
# python内置的values()函数返回一个字典中所有的值。
# 即只返回{key0:value0,key1:value1}中的value0、value1……(1)关于shape的详细使用可见:
http://t.csdn.cn/snq22
(2)data.iloc[:,] 逗号前面是关于行的 [ : ]代表行全选 逗号后面是关于列的
(3)np.matrix()是将数据转化为矩阵
(4)这里的数据是否使用 .values()不是很清楚 但不影响矩阵生成
4.建立一个2维度矩阵用来存放参数 下面的theta都代表θ、
5.关于为什么Insert后面会解释
theta=np.matrix([0,0])#建立一个空矩阵theta 代表参数θ5.计算代价函数J(Ѳ)
这个题目中只有两个参数
这时候我们就知道为什么使用insert来插入一列了
#——————————————————————————下面是计算代价函数J(Ѳ)——————————————————————
def computeCost(X,Y, theta):
inner = np.power(((X * theta.T) - Y), 2)
return np.sum(inner) / (2 * len(X)) #len(x)为行数 也就是公式中的m6.最优梯度下降
temp=theta 代表的是参数θ
paeameters代表的是参数θ的个数 方便在for in rang(parameters)中进行迭代循环
#——————————————————————————下面是梯度下降——————————————————————
def gradientDescent(X,Y,theta,alpha,iters): #梯度下降算法 alpha学习率 iters迭代次数
temp=np.matrix(np.zeros(theta.shape)) #np.zeros函数的作用返回来一个给定形状和类型的用0填充的数组
parameters=int(theta.flatten().shape[1]) #flatten()将多维降为一维函数 统计theta的元素个数
#parameters表示的是参数θ的个数
cost=np.zeros(iters)#保存迭代后的cost
for i in range(iters):
error=(X * theta.T) - Y #error 差值
for j in range(parameters):
term=np.multiply(error,X[:,j]) #X[:,j]抽取所有的行 以及第j列
temp[0, j] = theta[0, j] - ((alpha / len(X)) * np.sum(term))
theta = temp
cost[i] = computeCost(X, Y, theta)
return theta,cost
代码中的
6.输入参数
alpha=0.01 #alpha学习率
iters=1000 #iters迭代次数
g, cost= gradientDescent(X, Y, theta, alpha, iters)
print(g) #输出最终的参数
print(computeCost(X, Y, g))#使用拟合值来计算代价函数(误差)输出结果:
[[-3.24140214 1.1272942 ]]
4.515955503078914
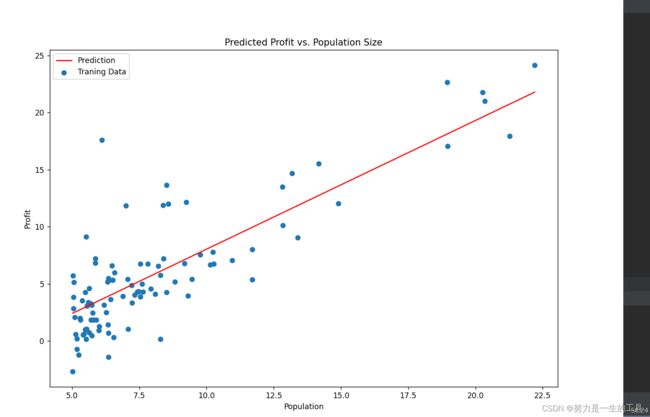
7.绘图
#——————————————————————————下面是绘图——————————————————————
x = np.linspace(data.Population.min(), data.Population.max(), 100)
f = g[0, 0] + (g[0, 1] * x) #g[0,0] 代表的是theta0 g[0,1] 代表的是theta1
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()
#下面是代价函数曲线
fig,ax=plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters),cost,'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()
注意:关闭第一张图才能打开第二张图片
对于多参数的线性回归仍然适用
二,正规方程的用法
import numpy as np
import pandas as pd
path ='ex1data1.txt'
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])
data.insert(0,'Ones',1)
clos=data.shape[1]
X=data.iloc[:,0:clos-1]
Y=data.iloc[:,clos-1:clos]
X=np.matrix(X)
Y=np.matrix(Y.values)
def normalEqn(X,Y):
thta=np.linalg.inv(X.T@X)@X.T@Y #X.T@X等价于X.T.dot(X)
return thta
final_theta2=normalEqn(X,Y)
print(final_theta2)结果:
[[-3.89578088]
[ 1.19303364]]