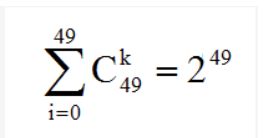#《机器学习》_周志华(西瓜书)&南瓜书__第1章 绪论 _第2章 模型评估与选择
待做:
- 理解习题2.5
- 补充修改
西瓜书: 机器学习 周志华
20世纪80年代: 符号学习 机器学习的主流
20世纪90年代: 统计机器学习
符号智能 统计智能
统计学 大数据
计算能力的大幅提高
认知科学研究
统计机器学习算法都是基于样本数据独立同分布的假设。
迁移学习
符号(离散)->统计(连续) 概率统计
概率和统计 VS 代数和逻辑
大数据分析: 收集、分析、预测
- 1-3章: 机器学习基础知识
- 4-10章: 经典而常用的机器学习方法
- 11-16章:进阶知识
除了前3章,后续各章 均相对独立。
对学科相关的重要人物和事件有一定了解,将会增加读者对该学科的认识。
观其大略——> 顾及细微
信息搜索, 知道自己在找什么,地形图 按图索骥
初级地形图
读者由本书初入门径后,不妨搁书熟习“套路”,数月后再阅,于原不经意处或能有所得。
问题:从习题总结,从后往前
1、分类器性能度量有哪些?
2、没有免费的午餐 定理 怎么理解?
3、书中是怎么推导和证明的
4、机器学习是什么? 什么样的东西可以归结为机器学习?
5、归纳偏好?
6、版本空间?
7、析和范式?
第1章 绪论
目标:这学期狠下了工夫,基础概念弄得清清楚楚,算法作业也是信手拈来,这门课成绩一定差不了。
机器学习:研究如何通过计算的手段,利用经验来改善系统自身的性能。
从数据中 产生 模型
Mitchell, 1997:
假设用P来评估计算机程序在某类任务T上的性能,若一个程序通过利用经验E在T中任务上获得了性能改善,则我们就说关于T和P,该程序对E进行了学习。
P:Performance
T: Task
E: Experience
基本术语:
属性(attribute)或特征(feature)
label (标记) 标签
D = { x 1 , x 2 , . . . , x m } : m 个 示 例 的 数 据 集 D=\left\{x_1, x_2,...,x_m\right\} :m个示例的数据集 D={x1,x2,...,xm}:m个示例的数据集
d个属性, x i = { x i 1 ; x i 2 ; . . . ; x i d } x_i=\left\{x_{i1};x_{i2};...;x_{id}\right\} xi={xi1;xi2;...;xid}是d维样本空间中的 χ χ χ中的一个向量,其中 x i j x_{ij} xij是 x i x_i xi在第 j j j个属性上的取值。d为样本 x i x_i xi的维数。
泛化: 适用于新样本,很好地反映出整个样本空间的特性。
1.3 假设空间
学习过程: 在所有假设组成的空间中进行搜索的过程。
搜索目标是找到与训练集匹配的假设,即能够将训练集中的瓜判断正确的假设。
现实: 有很大的假设空间
学习过程: 训练样本有限。
可能有多个假设与训练集一致,即存在一个与训练集一致的“假设集合”,称为版本空间。
- 注意版本空间是 假设的集合
1.4 归纳偏好
奥卡姆剃刀(Occam’s razor):若有多个假设与观察一致,则选最简单的那个。
什么样的模型更好?
- 算法的归纳偏好是否与问题本身匹配。
@没有免费的午餐 定理 推导:
假设样本空间 X \mathcal{X} X和假设空间 H \mathcal{H} H都是离散的.
P ( h ∣ X , L a ) P(h|X,\mathfrak{L}_a) P(h∣X,La):算法 L a \mathfrak{L}_a La基于训练 X X X产生假设 h h h的概率,
f f f:希望真实学习的真实目标函数
L a \mathfrak{L}_a La在训练集之外的所有样本上的误差:
E o t e ( L a ∣ X , f ) = ∑ h ∑ x ∈ X − X P ( x ) I ( h ( x ) ≠ f ( x ) ) P ( h ∣ X , ∣ L a ) E_{ote}(\mathfrak{L}_a|X,f)=\sum\limits_h\sum\limits_{x\in\mathcal{X}-X}P(x)\mathbb{I}(h(x)\neq f(x))P(h|X,|\mathfrak{L}_a) Eote(La∣X,f)=h∑x∈X−X∑P(x)I(h(x)=f(x))P(h∣X,∣La)
NFL定理(No Free Lunch Theorem ): 无论算法1多聪明,算法2多笨拙,两者的期望性能相同。
- 重要前提: 所有"问题’'出现的机会相同,或所有问题同等重要。
通常:只关注自己正试图解决的问题
假设真实目标函数 f f f是均匀分布的。
没有免费的午餐 理解
1、 脱离具体问题,空泛地谈论"什么学习算法更好"毫无意义。
2、考虑所有潜在的问题,则所有学习算法都一样好。
3、要谈论算法的相对优劣,必须要针对具体的学习问题。
决定: 学习算法自身的归纳偏好与问题与问题是否相配。
1.5 发展历程
1、20世纪50年代-70年代初: 推理期
智能==具有逻辑推理能力
作品: 逻辑理论家程序,通用问题求解程序。
——> 实现机器智能 ,需要使机器拥有知识
2、20世纪70年代中期: 知识期
专家系统
——>机器自己学习
3、20世纪80年代: 学习期
从样例中学习 符号主义学习、基于神经网络的连接主义学习
决策树 基于逻辑的学习。
4、20世纪90年代中期: 统计学习
支持向量机, 核方法。
5、21世纪初: 深度学习
大数据 + 计算能力提高
机器学习:不显式编程地赋予计算机能力的研究领域。
- 1952年, 萨缪尔跳棋程序。
P14
理论+ 实验+ 计算。
机器学习、云计算。众包。
数据挖掘: 数据库、机器学习、统计学。
P15
自动驾驶:
输入: 车载传感器收到的信息。
输出: 方向、刹车、油门的控制行为。
P16
SDM是稀疏编码机制在视觉、听觉、嗅觉功能的脑皮层中广泛存在。
P17
奥卡姆剃刀原则主张选择与经验观察一致的最简单假设。
习题
1.1
1.1 表1.1中若只包含编号为1和4的两个样例,试给出相应的版本空间。
版本空间(version space): 与训练集一致的假设集合。
1.色泽=青绿;根蒂=蜷缩;敲声=浊响
2.色泽=青绿;根蒂=蜷缩;敲声=*
3.色泽=青绿;根蒂=*;敲声=浊响
4.色泽=青绿;根蒂=*;敲声=*
5.色泽=*;根蒂=蜷缩;敲声=浊响
6.色泽=*;根蒂=蜷缩;敲声=*
7.色泽=*;根蒂=*;敲声=浊响
这7种情况都可以认为是好瓜。
1.2
1.2 与使用单个合取式来进行假设表示相比,使用"析合范式"将使得假设空间具有更强烈的表示能力,例如


针对表1.1 : 色泽2种、根蒂3种、敲声3种
1、单个合取式
假设个数: (2+1)×(3+1)×(3+1)+1=49
①不含通配符的假设:2×3×3=18种
②含一个通配符的假设:2×3+2×3+3×3=21种
③含两个通配符的假设:2+3+3=8种
④含三个通配符的假设:1种
再加上 空假设
1.3
1.3 若数据包含噪声,则假设空间中有可能不存在与所有训练样本都一致的假设。在此情形下,试设计一种归纳偏好用于假设选择。
根据少数服从多数原则,且尽量优先正例情形,删除部分样本。
1.4
1.4 本章在论述“没有免费的午餐”定理时,默认使用了“分类错误率”作为性能度量来对分类器进行评估。若换用其他性能度量 ℓ \ell ℓ,则式(1.1)将改为
E o t e ( L a ∣ X , f ) = ∑ h ∑ x ∈ X − X P ( x ) ℓ ( h ( x ) , f ( x ) ) P ( h ∣ X , ∣ L a ) E_{ote}(\mathfrak{L}_a|X,f)=\sum\limits_h\sum\limits_{x\in\mathcal{X}-X}P(x)\ell(h(x),f(x))P(h|X,|\mathfrak{L}_a) Eote(La∣X,f)=h∑x∈X−X∑P(x)ℓ(h(x),f(x))P(h∣X,∣La),
试证明"没有免费的午餐"仍成立。
根据原来的定义,且同样是针对分类问题,那么类似的,修改后的函数也是不是1就是0。仍成立。
1.5
1.5 试述机器学习能在互联网搜索的哪些环节起什么作用。
1、根据浏览历史记录优化推荐
2、排序
3、广告
4、建立输入与输出之间的关系
问题:
1、留出法?
2、10折交叉验证法和留一法?区别?
3、F1值,BEP值?
4、真正例率(TPR)、假正例率(FPR)与查准率( P P P)、查全率( R R R)?
5、错误率与ROC曲线
6、ROC曲线 代价曲线
7、 χ 2 \chi^2 χ2检验过程
8、Friedman检验
第2章 模型评估与选择
2.1 经验误差与过拟合
训练误差/经验误差
目标: 从训练样本中尽可能学出适用于所有潜在样本的普遍规律。
过拟合: 把训练样本自身的一些特点当作了所有潜在样本都具有的一般性质。
欠拟合 应对方法:
- 在决策树学习中扩展分支。
- 在神经网络学习中增加训练轮数。
2.2 评估方法
测试集应尽可能与训练集互斥
- 测试样本尽量不在训练集中出现、未在训练过程中使用过。
从数据集 D D D中产生出训练集 S S S和测试集 T T T。
2.2.1 留出法(hold-out)
分层采样
单次使用留出法得到的估计结果往往不够稳定可靠。
将大约2/3-4/5的样本用于训练
测试集至少应含30个样例
2.2.2 交叉验证法(cross validation)
数据集 D D D中包含m个样本,若令 k = m k=m k=m,留一法(Leave-One-Out) :
1、留一法不受随机样本划分方式的影响
2、留一法使用导电训练集只比初始数据集少一个样本
- 留一法中被实际评估的模型与期望评估的用D训练出来的模型很相似。
- 评估结果较准确
3、数据集较大时,训练模型的计算开销难以忍受。
2.2.3 自助法(bootstrapping)
留出法和交叉验证:保留了一部分样本用于测试
- 问题: 训练样本规模不同导致估计偏差。
目标: 减少训练样本规模不同造成的影响,同时高效地进行实验估计。
可重复采样/可放回采样
样 本 在 m 次 采 样 中 始 终 不 被 采 到 的 概 率 是 ( 1 − 1 m ) m 样本在m次采样中始终不被采到的概率是(1-\frac{1}{m})^m 样本在m次采样中始终不被采到的概率是(1−m1)m
lim m − > ∞ ( 1 − 1 m ) m = 1 e ≈ 0.368 \lim\limits_{m -> \infty}(1-\frac{1}{m})^m=\frac{1}{e}\approx0.368 m−>∞lim(1−m1)m=e1≈0.368
有数据总量约1/3的、没在训练集中出现的样本用于测试。
1、自助法在数据集较小,难以有效划分训练集/测试集时很有用。
2、自助法产生的数据集改变了初始数据集的 分布,会引入估计偏差。
在初始数据量足够时,留出法和交叉验证更常用
2.2.4 调参与最终模型
计算开销 VS 性能估计
测试集: 估计模型在实际使用时的泛化能力。
训练数据=训练集+验证集
- 基于验证集上的性能进行模型选择和调参。
2.3 性能度量: 评价模型泛化能力
什么样的模型是好的:取决于算法、数据、任务需求。
回归_均方误差
学 习 器 预 测 结 果 f ( x ) , 真 实 标 记 y : 学习器预测结果f(x),真实标记y: 学习器预测结果f(x),真实标记y:
均 方 误 差 : E ( f ; D ) = 1 m ∑ i = 1 m ( f ( x i ) − y i ) 2 均方误差:E(f;D)=\frac{1}{m}\sum\limits_{i=1}^{m}(f(x_i)-y_i)^2 均方误差:E(f;D)=m1i=1∑m(f(xi)−yi)2
数 据 分 布 D 和 概 率 密 度 函 数 p ( ⋅ ) 数据分布\mathcal{D}和概率密度函数p(·) 数据分布D和概率密度函数p(⋅)
均 方 误 差 : E ( f ; D ) = ∫ x ∼ D ( f ( x ) − y ) 2 p ( x ) d x 均方误差:E(f;\mathcal{D})=\int_{x\sim\mathcal{D}}(f(x)-y)^2p(x)dx 均方误差:E(f;D)=∫x∼D(f(x)−y)2p(x)dx
2.3.1 错误率与精度
分类任务:
错误率:分类错误的样本数占样本总数的比例。
E ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) ≠ y i ) E(f;D)=\frac{1}{m}\sum\limits_{i=1}^m\mathbb{I}(f(x_i)\neq y_i) E(f;D)=m1i=1∑mI(f(xi)=yi)
精度: 分类正确的样本数占样本总数的比例。
a c c ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) = y i ) = 1 − E ( f ; D ) acc(f;D)=\frac{1}{m}\sum\limits_{i=1}^m\mathbb{I}(f(x_i)= y_i)=1-E(f;D) acc(f;D)=m1i=1∑mI(f(xi)=yi)=1−E(f;D)
更一般
数 据 分 布 D 和 概 率 密 度 函 数 p ( ⋅ ) 数据分布\mathcal{D}和概率密度函数p(·) 数据分布D和概率密度函数p(⋅)
错 误 率 : E ( f ; D ) = ∫ x ∼ D I ( f ( x ) ≠ y ) p ( x ) d x 错误率:E(f;\mathcal{D})=\int_{x\sim\mathcal{D}}\mathbb{I}(f(x)\neq y)p(x)dx 错误率:E(f;D)=∫x∼DI(f(x)=y)p(x)dx
精 度 : a c c ( f ; D ) = ∫ x ∼ D I ( f ( x ) = y ) p ( x ) d x = 1 − E ( f ; D ) 精度:acc(f;\mathcal{D})=\int_{x\sim\mathcal{D}}\mathbb{I}(f(x)=y)p(x)dx=1-E(f;\mathcal{D}) 精度:acc(f;D)=∫x∼DI(f(x)=y)p(x)dx=1−E(f;D)
2.3.2 查准率、查全率与 F 1 F1 F1
信息检索、Web搜索:
- 检索出的信息中有多少比例是用户感兴趣的。
- 用户感兴趣的有多少被检索出来了。
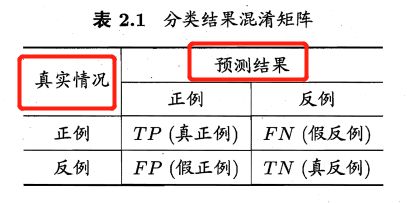
真正例(true positive, TP)
假正例(false positive, FP)
真反例(true negative, TN)
假反例(false negative, FN)
查准率/准确率 P P P: P = T P T P + F P P=\frac{TP}{TP+FP} P=TP+FPTP
- 预测的正例中,实际为正例的比例。
查全率/召回率 R R R: R = T P T P + F N R=\frac{TP}{TP+FN} R=TP+FNTP
- 实际正例里真正找回来的比例
查准率和查全率是矛盾的度量。

F 1 度 量 : 基 于 查 准 率 与 查 全 率 的 调 和 平 均 F1度量:基于查准率与查全率的调和平均 F1度量:基于查准率与查全率的调和平均
F 1 = 2 × P × R P + R = 2 × T P 样 例 总 数 + T P − T N F1=\frac{2×P×R}{P+R}=\frac{2×TP}{样例总数+TP-TN} F1=P+R2×P×R=样例总数+TP−TN2×TP
1 F 1 = 1 2 ⋅ ( 1 P + 1 R ) \frac{1}{F1}=\frac{1}{2}·({\frac{1}{P}+\frac{1}{R}}) F11=21⋅(P1+R1)
商品推荐,查准率更重要;
逃犯信息检索系统,查全率更重要。
F β F_β Fβ:加权调和平均,与算术平均和几何平均相比,调和平均更重视较小值。
F β = ( 1 + β 2 ) × P × R ( β 2 × P ) + R F_β=\frac{(1+β^2)×P×R}{(β^2×P)+R} Fβ=(β2×P)+R(1+β2)×P×R
1 F β = 1 1 + β 2 ⋅ ( 1 P + β 2 R ) \frac{1}{F_β}=\frac{1}{1+β^2}·({\frac{1}{P}+\frac{β^2}{R}}) Fβ1=1+β21⋅(P1+Rβ2)
1、 β β β=1,标准的 F 1 F1 F1
2、β>1, 查全率更大影响
3、β<1, 查准率更大影响。
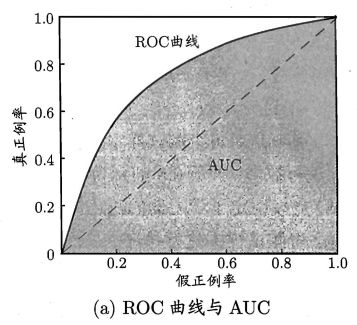
2.3.3 ROC与AUC
ROC(Receiver Operating Characteristic), 受试者工作特征。
根据学习器的预测结果对样例进行排序,按此顺序逐个把样本作为正例进行预测,每次计算出两个重要值。
真正例率(True Positive Rate, TPR): T P R = T P T P + F N TPR=\frac{TP}{TP+FN} TPR=TP+FNTP
- 实际正例中 被判为 正例 的 比例
假正例率(False Positive Rate, FPR): F P R = F P T N + F P FPR=\frac{FP}{TN+FP} FPR=TN+FPFP
- 实际负例中 被判为 正例 的 比例
AUC(Area Under ROC Curve)
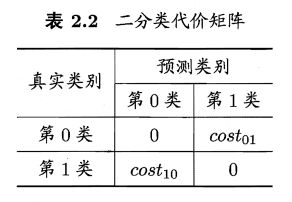
2.3.4 代价敏感错误率与代价曲线
2.4 比较检验
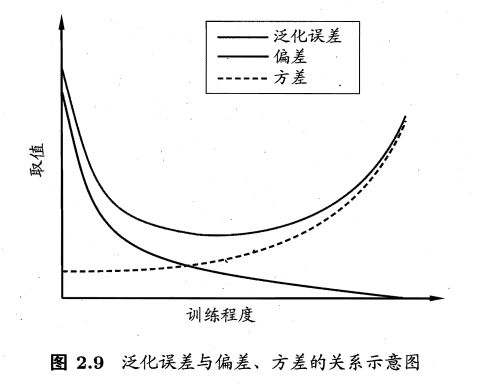
2.5 偏差与方差
偏差:学习算法的期望预测与真实结果的偏离程度
- 学习算法本身的拟合程度。
方差:数据扰动造成的影响
噪声:在当前任务上任何学习算法所能达到的的期望泛化的误差的下界。
- 刻画了学习问题本身的难度。
泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度共同决定。
1、训练不足时,学习器的拟合能力不够强,训练数据的扰动不足以使学习器产生显著变化,此时偏差占主导。
2、训练程度充足之后,学习器的拟合能力已非常强,训练数据发生的轻微扰动都会导致学习器发生显著变化,若训练数据自身的、非全局的特性被学习器学到了,将发生过拟合。
习题
2.1
2.1 数据集包含1000个样本,其中500个正例、500个反例,将其划分为包含70%样本的训练集和30%样本的测试集用于留出法评估,试估算共有多少种划分方式。
根据书本P25页的相关内容,训练/测试集的划分要尽可能保持数据分布的一致性。分层采样后 S S S应该包含350个正例(500×70%),350个反例; T T T应该包含150个正例(500×30%),150个反例.
目标: 从500个正例里抽150个正例,从500个反例里抽150个反例作为测试集,其余的作为训练集。
方法数有 ( C 500 150 ) 2 (C_{500}^{150})^2 (C500150)2
2.2
2.2 数据集包含100个样本,其中正、反例各一半,假定学习算法所产生的模型是将新样本预测为训练样本数较多的类别(训练样本数相同时进行随机猜测),试给出用10折交叉验证法和留一法分别对错误率进行评估所得的结果。
由题意,已知学习算法所产生的模型是将新样本预测为训练样本数较多的类别(训练样本数相同时进行随机猜测)。
此外,错误率(P29)是分类错误的样本数占样本总数的比例。
10折交叉验证:分成的10个子数据集(每个子数据集包含5个正例,5个反例),每个子集当一次测试集,由于训练集和测试集的数据分布都是正反例各占一半,所以每折错误率都是5/10=50%。综合来看,错误率为50%×10/10=50%。
留一法:由于留一法是交叉验证法的特殊情形,类似的,划分成100个子集,每个子集当一次测试样本。当测试样本为1个正例时,说明对应的测试集是45个正例和50个反例,此时测试的错误率为100%;当测试样本为1个反例,说明对应的测试集是50个正例,45个反例,测试的错误率为1/1=100%。综合错误率为100%×100/100=100%。
2.3
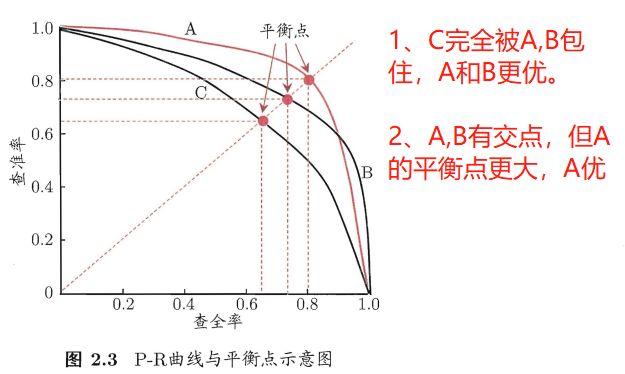
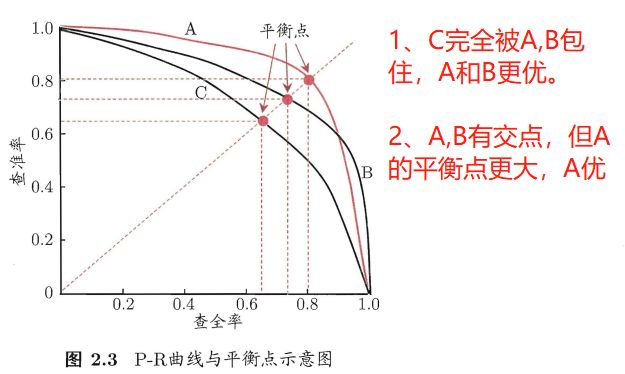
2.3 若学习器A的F1值比学习器B高,试析A的BEP值是否也比B高。
F 1 = 2 × P × R P + R F1=\frac{2×P×R}{P+R} F1=P+R2×P×R是比BEP(Break-Event Point,平衡点)进阶的度量指标,为查准率与查全率之间的调和平均。
BEP是查准率=查全率时的取值。
F 1 A = 2 × P A 2 2 × P A = P A F1_A=\frac{2×P_A^2}{2×P_A}=P_A F1A=2×PA2×PA2=PA,
类似的, F 1 B = P B F1_B=P_B F1B=PB
显然,若是学习器A的F1值比学习器B高( F 1 A > F 1 B F1_A>F1_B F1A>F1B),A的BEP值也会比B高( P A > P B P_A>P_B PA>PB)。
按照题目的说法,应该是有一个前提,学习器A的F1值不管P和R怎么取值都比学习器B高,这样的话只考虑平衡点位置就可以了。
2.4
2.4 试述真正例率(TPR)、假正例率(FPR)与查准率( P P P)、查全率( R R R)之间的联系。
查准率 P = T P T P + F P P=\frac{TP}{TP+FP} P=TP+FPTP,预测正例中,实际为正例的比例。
查全率 R = T P T P + F N R=\frac{TP}{TP+FN} R=TP+FNTP,实际正例中,预测为正例的比例。
真正例率 T P R = T P T P + F N TPR=\frac{TP}{TP+FN} TPR=TP+FNTP,与查全率一样
假正例率 F P R = F P T N + F P FPR=\frac{FP}{TN+FP} FPR=TN+FPFP,实际反例中,预测为正例的比例
- 看着和查全率有点关系,在医学上属于误诊率(本来是健康的,诊出疾病来)。
- 从整体来看,更关心正例的比例情况
2.5???
2.5 试证明式(2.22).
2.6
2.6 试述错误率与ROC曲线的联系
错误率是分类错误的样本数占样本总数的比例。
ROC曲线是受试者工作特征曲线。曲线上的每一个点对应一个错误率。
2.7
2.7 试证明任意一条ROC曲线都有一条代价曲线与之对应,反之亦然。

2.8
2.8 Min-max规范化和z-score规范化是两种常用的规范化方法。

| 规范化方法 | 优点 | 缺点 |
|---|---|---|
| min-max | 1、计算相对简单;2、当新样本进来时,只有当新样本大于原最大值或者小于原最小值时,才需要重新计算规范化之后的值。 | 易受异常点影响。 |
| z-score | 对异常值敏感低 | 每次新样本进来都需要重新计算规范化。 |
|
2.9
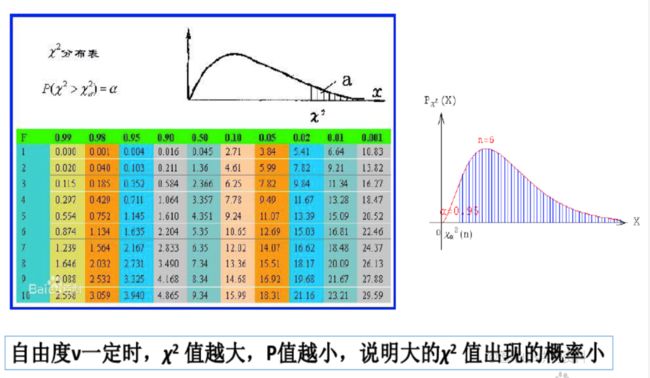
2.9 试述 χ 2 \chi^2 χ2检验过程。
计算参考链接
χ 2 \chi^2 χ2检验,即卡方检验。
一般用于统计样本的实际观测值与理论推断值之间的偏离程度,实际观测值与理论推断值之间的偏离程度判断取决于卡方值的大小,卡方值越大,越不符合;卡方值越小,偏差越小,越趋于符合,若两个值完全相等时,卡方值就为0,表明理论值完全符合。
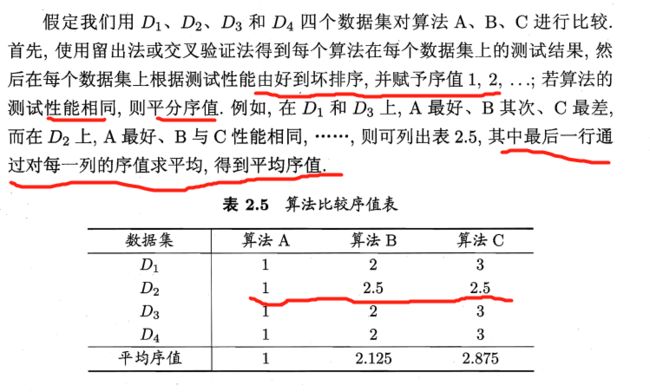
2.10
2.10 试述在Friedman检验中使用式(2.34)与(2.35)的区别。
LaTeX 字符链接
https://blog.csdn.net/weixin_42612337/article/details/103037333