Generative Interventions for Causal Learning——因果推断干预图像生成过程

随着近期因果推断的热门，一系列通过因果干预网络进行因果特征学习的模型也被提出。这些模型大多是通过对输入输出数据之间的因果图进行分析，通过人为切断非因果部分与网络输出结果之间的相关性，从而达到将传统模型转换为因果模型的效果。本文便是近期提出的一个用于训练因果分类器的方法。

本文出发点

传统的模型训练方法通过是基于数据驱动的统计学习方法，在模型训练的过程中并不会对因果特征和干扰特征加以区分，这便会造成许多隐性的问题，尤其，当训练数据分布于测试数据分布不相符时，这些问题便会暴露出来。一个典型的例子，在ImageNet上经过充分训练的最优秀的分类器，虽然在ImageNet上可以取得优秀的成绩，但是在ObjectNet数据集(包含ImageNet的object元素，但是去掉了其中的背景等无关信息)上进行测试，模型性能通常会下降近40%。分类器是通过对输入图像进行特征提取而实现的，在这个过程中如果只有与label相关的因果特征应该被提取，那么模型的鲁棒性就将大大提升。为了实现这个目的，传统的手段是对训练数据进行随机对照试验或干预，然而这对于传统分类任务是不行的，因为我们无法对已知图像(我们的训练集)进行干预，并且手动收集相匹配的干预图像成本非常高。本文的想法源于这么一个事实：对于label无关的特征变量，当我们在高维特征空间对其进行干预时，其干预结果会在低维图像空间以视觉的方式反映出来。因此我们可以通过构建一个生成器，通过对高纬特征空间中的干扰特征部分进行随机干预，保留label特征(例如在条件GAN中固定y不变)，从而生成逼真的各种随机干预图像，消除干扰特征与label之间虚假的相关性。此外这里还要提一点，本文将这种生成数据方式看做一种尊重因果关系的数据增强方法，作者将传统的数据增强方法看做是仅仅在原始数据分布上进行增强，也就是只能生成与训练集相符的分布，因此不能对viewpoint，background等因素进行增强，终究是跳不出干扰特征的虚假相关性的问题，本文却可以。因此本文的写作思路是按照数据增强来写的，后面的实验对比也是与数据增强方法来进行对比的。

本文的因果分析

上面已经提到了，本文的基本思路是通过训练一个条件生成网络(e.g. cGAN)，通过对生成过程中高维空间中的干扰特征进行人为干预来进行，接下来我们通过公式化和因果图的方式来具体说明。对于一个在训练数据集上训练好的生成网络(e.g. a cGAN $G(.)$ trained on ImageNet)，我们通过将一个随机的label $y$和noise $h_0$输入，获得一个标准图像$x=G(h_0,y)$，之后我们将一个干扰变量$z$施加到$h_0$上，得到一个干扰noise $h_0^{\ast }$，然后我们再将其输入到网络中，获得$x^{\ast }=G(h_0^{\ast },y)$，这个$x^{\ast }$和$x$在图像label上相同，但是却在某个干扰特征e.g. background, viewpoint上面发生了变化，之后我们用这些生成图像对我们的分类器进行训练，就可以排除掉这些干扰特征与label的虚假相关性。我们之后还可以训练一个网络从$x^{\ast }$中对$z$进行预测，然后通过训练的网络对一系列的标准图像甚至是真实图像进行预测，将预测结果与其相对应的label $y$训练一个分类器，直观的，我们这个分类器的性能就可以代表$z$与$y$的相关性。因为$z$和$y$理论上是没有因果关系的如果我们的分类结果好于随机那就说明$z$和$y$有着相关性。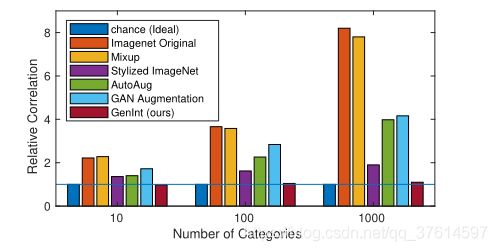
这张图反映了不同的训练数据对$z$和$y$的相关性的影响，其中相关性越高，反映了其中的干扰特征$z$与label $y$的虚假相关性越大。

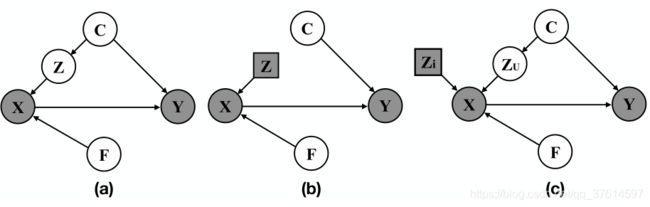
接着给出本文的一个因果图。其中$X$是训练集中的图像，$Y$是对应的预测据结果，$F$是与$Y$有着因果关系的特征量，$Z$则是与$Y$没有因果关系的干扰变量。$C$是confounding，通过其对$Z$和$Y$的因果关系将二者联系了起来，产生了虚假的相关性。其中还需要注意一点，图中只有灰色部分是我们可见的，因此我们不能直接得到$Y\perp F|X$，因为$F$是通过$X$才与$Y$产生因果关系，而$Z\to X\to Y$，$Z$与$Y$却没有因果关系。
我们通过用$do()$来描述两个变量的因果关系，因为我们只能玩概率模型，也就是我们所获得的是一种联合分布$P(X,Y)$，所以我们要让概率模型尽量逼近因果模型，如果对应上图，也就是我们要让$P(Y|do(X))=P(Y|X)$尽可能成立。如何让这个式子成立呢，一个显著的方式就是让$F$保持不变的前提下，尽量让$Z$成为一个独立的变量，这样$Z$和$C$的联系就会被断开，也就是上图(b)的情况。在物理上实现这种操作的方式是手动调整相机的角度或是object的背景，而在这篇文章中，我们使用的方式是对生成器进行人为的扰动(在这个生成过程中，这个图中的$F$可以看做是输入到生成网络中的$y$，图中的$Z$可以看做是其他变量$h_0$)。接下来作者通过公式和定理给出了扰动方法：
通过已存在的生成器，在不对其干涉的前提下，我们可以给出这个一个不等式$$P(x,y)\le P(y|do(x))\le P(x,y)+1-P(x)$$
通过上面的分析我们看出，对于传统的数据生成方式，由于生成结果并未对$Z$加以干涉，因此即使获得再多的训练数据也不能改变上面的因果边界，要想使得上面的因果边界变得更紧，只能通过训练对$Z$进行干涉的数据，因为这样的数据减弱了$Z$与$Y$之间的虚假相关性。但是这里又要面临一个主要的问题，我们无法对全部的$Z$都一一进行扰动，那么我们选择什么样的$Z$进行扰动呢，因果效应边界(Causal Effect Bound)定理给出了说明：
具体证明略
上面的定理就是告诉我们，通过选择与$X$关系更密切的$Z$，对这样的$Z$进行扰动，我们得到的边界将会更紧，也就是，我们要$\max P(X|Z)$。

本文的实施方法

本文的本质目的还是要训练一个对图像的分类器，因此本文的分类器其目标函数为：

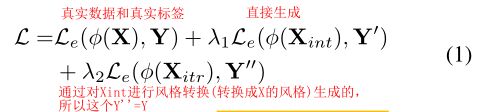
第一项就是普通的真实图像和label，$\varphi$是分类器，$L_e$是交叉熵损失。
第二项中主要说一下$X_{int}$和$Y^{\prime }$是什么东西：我们假设在数据生成的时候，第$i$层的高纬特征是$h_i$，本文使用的条件GAN——BIgGAN的生成过程就可以表示为$x=G(h_0,y)$, 其中$h_0\sim N(0,I)$。此外，BIgGAN学习的$h_i$，实际上是独立与label之外的，所以无论什么label，在保证其不变的情况下我们都可以通过对$h_i$进行干涉而产生相同的干涉效果，也就是在视觉空间上产生相同的视觉效果。通过这种方式，不改变类别，改变其他干扰特征，就可以使得$Z$与$C$独立，从而消除其对label的影响。之后我们通过控制三个量实现扰动：1、 The input noise $h_0$ is sampled from Gaussian noise truncated by value $t$，这句中的truncated by value $t$ 本人没读懂，跳过。2、变化方向。我们将变化最显著的第$j$个方向称为$r_j$，这些变化方向将会是正交的，并且代表了数据的主要变化。从直观上，这符合上面的理论分析。我们选出前$k$个$r_j$ $r_1,r_2,...,r_k$。3、沿着变化方向，我们在均匀分布$[-s,s]$上选取变化步长$s^{\prime }$。这样，对于BigGAN生成过程中的每个高纬特征量，我们都将其进行$h_i^{\ast }=h_i+\sigma s^{\prime }{r}_j-\mu$的变化，其中$\sigma$是$r$的标准差，$\mu$是抵消项，保证变化后的高纬特征在可控范围之内。我们将干涉过程用I来代替，生成干涉过程可以改写为$X_{int}=I(t,s,k,Y^{\prime })$。
之后再来说一下第三项，第三项是试图将训练集中的真实图像$X$也进行干涉。通常的做法是将其做一个BIgGAN的逆变换，再通过第二项的过程来生成，然而这样麻烦不说，生成的结果也是会丢失掉许多信息。作者通过一种更巧妙的方式，将第二项扰动后生成的数据作为模板，将其和真实图像进行风格转换。这样在获得了扰动信息的同时，还可以保留其自身的label，因此本项可以用：$X_{itr}=T(I(t,k,s,Y^{\prime }),X)$来表示，也就是$Y^{\prime \prime }=Y$，其中$T()$是风格转换网络。

实验结果分析

实验的开始，我们先来说一下几个特殊的数据集：
1、ObjectNet，上文说到，就是ImageNet去掉背景等干扰因素后的纯粹的object
2、ImageNet-C，对ImageNet进行15中常见的corruptions后的结果
3、ImageNet-V2，ImageNet的test版本，用于测试在ImageNet上训练的网络的泛化性

实验一（在ObjectNet进行测试的消融实验）

其中四个比较对象分别是只在ImageNet上训练的网络和三个对于本文提出的目标函数排列组合的数据进行训练的网络。可以看出本文的方法可以大大提高在ObjectNet上的分类精度(Std Augmentation一列)，同时对于Add Augmentation一列，本文提出的方法改进幅度更大，这说明本文的方法确实可以弥补传统增强方法的不足之处，或者说这种方法与传统数据增强方法是正交的。

实验二（在ImageNet-C上与传统数据增强方法进行的消融实验）

可以看到本文的方法在ImageNet上极大领先了传统数据增强方法，并且在绝大多数的corruptions下，本文的方法也是最好的。这里要重点说一下，虽然Stylized ImgNet在所有的baseline中是效果最好的，但是它的精度提升并不是其抓住了因果关系，而是其使得模型对干扰信息产生了过拟合，这一点作者通过额外的实验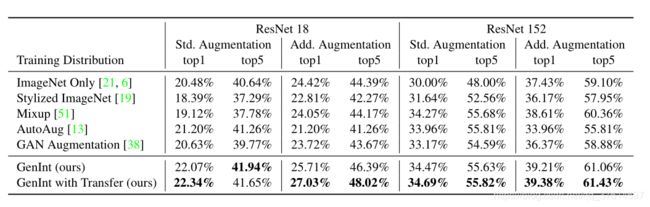
给出了证明。凡是弱于ImageNet Only的，统统是这个原因。

实验三（在ImageNet v2上的泛化能力）

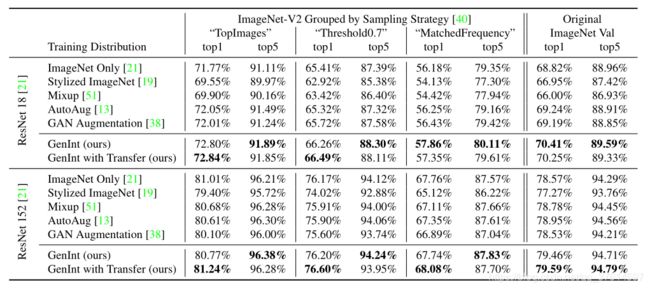
本方法的另一个不同于其他因果方法的卖点是，本文在增强了模型泛化能力的同时，并没有将模型在原数据集上的精度降低，对比很多因果模型，提高泛化性能难免意味着放弃一定的精度。
接下来是一些对理论分析进行验证类的实验

实验四（因果边界与分类精度之间的关系）

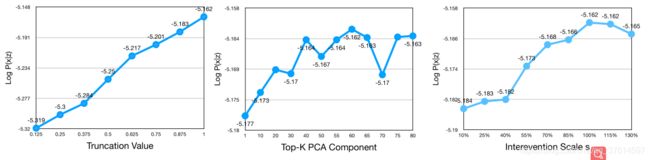
这里作者为了验证其理论分析的有效性。边界紧度我们不能直接进行调整，我们可以进行调整的只有干预的强度，为了说明更强的干预可以产生更紧的边界，作者先是给出了右边的图，也就是通过log likelihood来表示，$$logP(x|z)=\sum _i\sum _{x_j^{\prime }}log(P(x_i|x_j^{\prime })P(x_j^{\prime }|z))$$。之后作者又通过在更紧的边界上分类的精度对比，来验证了上文的理论正确性。

实验五（对三个超参数的消融）

分别对应目标函数第二项中的t、k、s，这里不再赘述。

实验六（干涉的生成结果比直接的生成结果训练效果好）

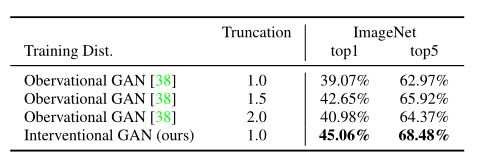
为了说明单纯的生成结果(不加干涉)不能使得模型得到很好的训练，这里作者将单纯训练的BIgGAN的生成结果与本文干涉的生成结果训练的分类器在ImageNet上进行了对比，效果显而易见，符合我们上面的分析。

实验七（Model Visualization）