机器学习四种调参方法总结
介绍
维基百科上说,“Hyperparameter optimization或tuning是为学习算法选择一组最优的hyperparameters的问题”。
本文转载于收藏 | 机器学习四种调参方法总结
ML工作流中最困难的部分之一是为模型找到最好的超参数。ML模型的性能与超参数直接相关。超参数调优的越好,得到的模型就越好。调优超参数可能是非常乏味和困难的,更像是一门艺术而不是科学。
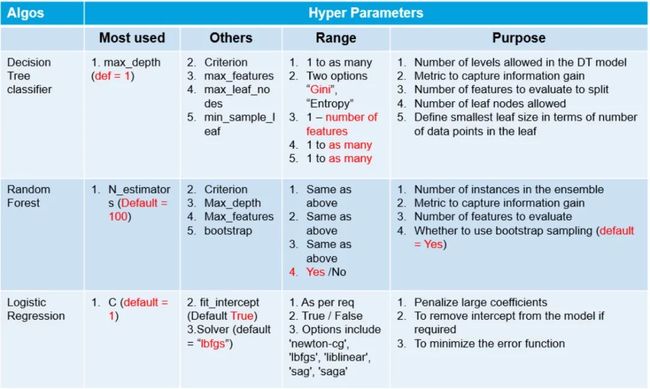
超参数
超参数是在建立模型时用于控制算法行为的参数。这些参数不能从常规训练过程中获得。在对模型进行训练之前,需要对它们进行赋值。
超参数的简单列表
目录
介绍
超参数
1. 传统手工搜索
2. 网格搜索
3. 随机搜索
4. 贝叶斯搜索
总结
1. 传统手工搜索
在传统的调参过程中,我们通过训练算法手动检查随机超参数集,并选择符合我们目标的最佳参数集。
我们看看代码:
#importing required libraries
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold , cross_val_score
from sklearn.datasets import load_wine
wine = load_wine()
X = wine.data
y = wine.target
#splitting the data into train and test set
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.3,random_state = 14)
#declaring parameters grid
k_value = list(range(2,11))
algorithm = ['auto','ball_tree','kd_tree','brute']
scores = []
best_comb = []
kfold = KFold(n_splits=5)
#hyperparameter tunning
for algo in algorithm:
for k in k_value:
knn = KNeighborsClassifier(n_neighbors=k,algorithm=algo)
results = cross_val_score(knn,X_train,y_train,cv = kfold)
print(f'Score:{round(results.mean(),4)} with algo = {algo} , K = {k}')
scores.append(results.mean())
best_comb.append((k,algo))
best_param = best_comb[scores.index(max(scores))]
print(f'\nThe Best Score : {max(scores)}')
print(f"['algorithm': {best_param[1]} ,'n_neighbors': {best_param[0]}]")
缺点:
-
没办法确保得到最佳的参数组合。
-
这是一个不断试错的过程,所以,非常的耗时。
2. 网格搜索
网格搜索是一种基本的超参数调优技术。它类似于手动调优,为网格中指定的所有给定超参数值的每个排列构建模型,评估并选择最佳模型。考虑上面的例子,其中两个超参数 k_value =[2,3,4,5,6,7,8,9,10] & algorithm =[ auto , ball_tree , kd_tree ,brute ],在这个例子中,它总共构建了9*4 = 36不同的模型。
让我们来了解一下sklearn的GridSearchCV是如何工作的:
from sklearn.model_selection import GridSearchCV
knn = KNeighborsClassifier()
grid_param = { 'n_neighbors' : list(range(2,11)) ,
'algorithm' : ['auto','ball_tree','kd_tree','brute'] }
grid = GridSearchCV(knn,grid_param,cv = 5)
grid.fit(X_train,y_train)
#best parameter combination
grid.best_params_
#Score achieved with best parameter combination
grid.best_score_
#all combinations of hyperparameters
grid.cv_results_['params']
#average scores of cross-validation
grid.cv_results_['mean_test_score']
缺点:
由于它尝试了超参数的每一个组合,并根据交叉验证得分选择了最佳组合,这使得GridsearchCV非常慢。
3. 随机搜索
使用随机搜索代替网格搜索的动机是,在许多情况下,所有的超参数可能不是同等重要的。随机搜索从超参数空间中随机选择参数组合,参数由n_iter给定的固定迭代次数的情况下选择。实验证明,随机搜索的结果优于网格搜索。
让我们来了解sklearn的RandomizedSearchCV是如何工作的:
from sklearn.model_selection import RandomizedSearchCV
knn = KNeighborsClassifier()
grid_param = { 'n_neighbors' : list(range(2,11)) ,
'algorithm' : ['auto','ball_tree','kd_tree','brute'] }
rand_ser = RandomizedSearchCV(knn,grid_param,n_iter=10)
rand_ser.fit(X_train,y_train)
#best parameter combination
rand_ser.best_params_
#score achieved with best parameter combination
rand_ser.best_score_
#all combinations of hyperparameters
rand_ser.cv_results_['params']
#average scores of cross-validation
rand_ser.cv_results_['mean_test_score']
缺点:
随机搜索的问题是它不能保证给出最好的参数组合。
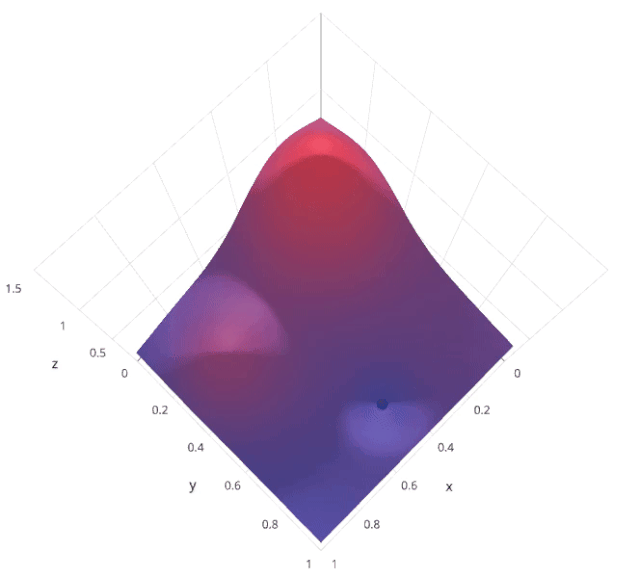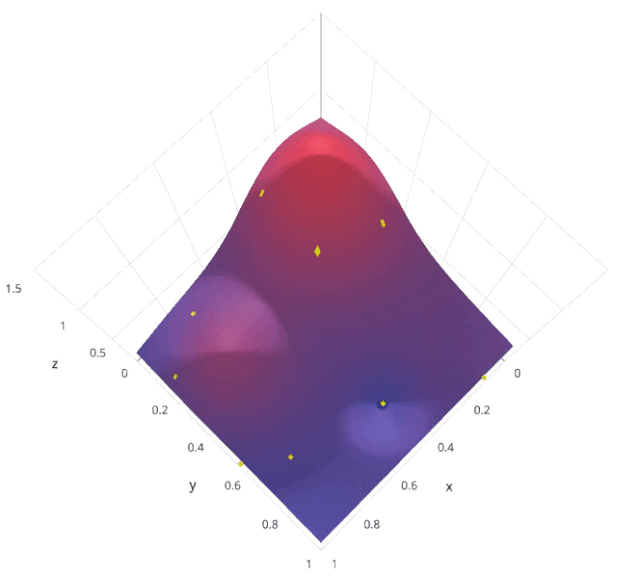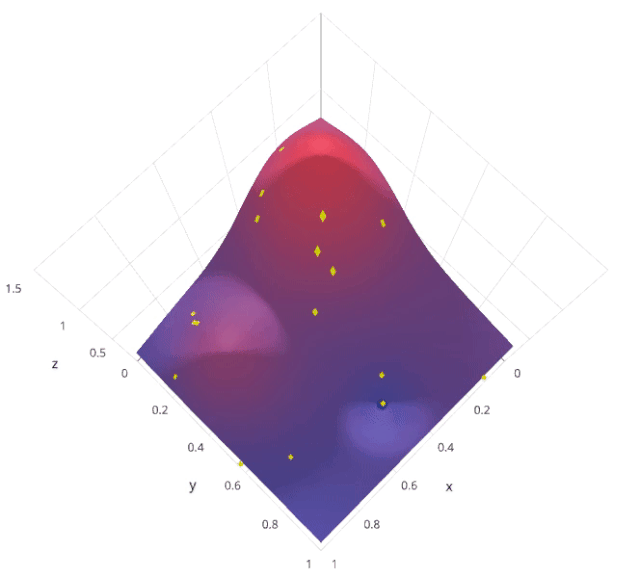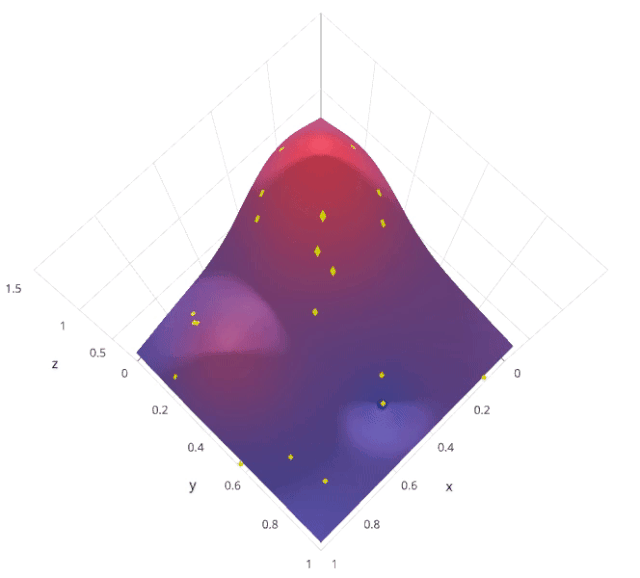
4. 贝叶斯搜索
贝叶斯优化属于一类优化算法,称为基于序列模型的优化(SMBO)算法。这些算法使用先前对损失 f 的观察结果,以确定下一个(最优)点来抽样 f。该算法大致可以概括如下。
-
使用先前评估的点 X 1:n,计算损失 f 的后验期望。
-
在新的点 X 的抽样损失 f,从而最大化f的期望的某些方法。该方法指定 f 域的哪些区域最适于抽样。
重复这些步骤,直到满足某些收敛准则。
让我们用scikit- optimization的BayesSearchCV来理解。
Installation: pip install scikit-optimize
from skopt import BayesSearchCV
import warnings
warnings.filterwarnings("ignore")
# parameter ranges are specified by one of below
from skopt.space import Real, Categorical, Integer
knn = KNeighborsClassifier()
#defining hyper-parameter grid
grid_param = { 'n_neighbors' : list(range(2,11)) ,
'algorithm' : ['auto','ball_tree','kd_tree','brute'] }
#initializing Bayesian Search
Bayes = BayesSearchCV(knn , grid_param , n_iter=30 , random_state=14)
Bayes.fit(X_train,y_train)
#best parameter combination
Bayes.best_params_
#score achieved with best parameter combination
Bayes.best_score_
#all combinations of hyperparameters
Bayes.cv_results_['params']
#average scores of cross-validation
Bayes.cv_results_['mean_test_score']
另一个实现贝叶斯搜索的类似库是bayesian-optimization。
Installation: pip install bayesian-optimization
缺点:
要在2维或3维的搜索空间中得到一个好的代理曲面需要十几个样本,增加搜索空间的维数需要更多的样本。
总结
在确定参数的最佳组合的保证和计算时间之间总是存在权衡。如果超参数空间(超参数个数)非常大,则使用随机搜索找到超参数的潜在组合,然后在该局部使用网格搜索(超参数的潜在组合)选择最优特征。