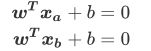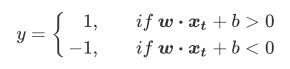机器学习入门基础（二）

不纯度

• 决策树的每个根节点和中间节点中都会包含一组数据（工作为公务员为某一个节点），在这组数据中，如果有某一类标签占有较大的比例，我们就说该节点越“纯”，分枝分得好。某一类标签占的比例越大，叶子就越纯，不纯度就越低，分枝就越好。
• 如果没有哪一类标签的比例很大，各类标签都相对平均，则说该节点”不纯“，分枝不好，不纯度高
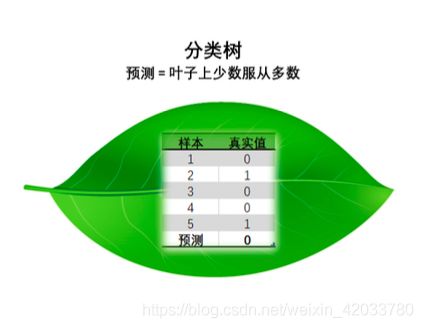
• 这个其实非常容易理解。分类型决策树在节点上的决策规则是少数服从多数，在一个节点上，如果某一类标签所占的比例较大，那所有进入这个节点的样本都会被认为是这一类别。具体来说，如果90%根据规则进入节点的样本都是类别0(节点比较纯)，那新进入该节点的测试样本的类别也很有可能是0。但是，如果51%的样本是0，49%的样本是1(极端情况)，该节点还是会被认为是0类的节点，但此时此刻进入这个节点的测试样本点几乎有一半的可能性应该是类别1。从数学上来说，类分布为(0,100%)的结点具有零不纯性，而均衡分布 (50%,50%)的结点具有最高的不纯性。如果节点本身不纯，那测试样本就很有可能被判断错误，相对的节点越纯，那样本被判断错误的可能性就越小。
  
• 如何计算不纯度？
  • 信息熵
• 信息论基础
  • 问题：现在有32支球队，然后猜出谁是冠军！
    • 如果我们不知道球队的任何信息情况下，我们可以这么猜：
    • 你可能会乱猜那么猜对的几率为1/32。
    • 如果你没猜错一次需要付出一定的代价，则你就会设计方法提升猜你对的几率而减少代价。
    • 每次折半猜，将32只球队以此编码为1-32，则第一次你会问，冠军在1-16中，在1-8中吗等等这样折半的猜，那么这样势必会减少猜错的几率，付出较少的代价。
    • 折半猜的话只需要猜log32=5次（底数为2）就可以知道结果啦。
    • 结论：我们已经知道32只球队猜对的代价为log32=5次，64只球队猜对的代价为log64=6次，以信息论的角度来讲的话，代价为5次或者代价为6次被称为代价为5比特或者代价为6比特。
    • 比特：就是信息论中信息度量的单位也叫做信息量。这个概念是由信息论的创始人【香农】提出的。
  • 重点：香农在信息论中提出信息量的值会随着更多有用信息的出现而降低
    • 继续猜冠军的问题：
      • 如果将32只球队的一些往期比赛胜负的数据进行公开，则《谁是冠军》的信息量的值肯定会小于5比特，其精准的信息量的值计算法则为：注意信息量的值在信息论中被称为信息熵
      • $H=-\sum _{i=1}^{n}p(x_i)lo{g}_{2}p(x_i)$
    • 公式解释：
      • 在谁是冠军例子中，n就是32，p(xi)就是某只球队获胜的概率，H为信息量的值叫做【信息熵】
      • 信息熵（entropy）：是一种信息的度量方式，表示信息的混乱程度，也就是说：信息越有序，信息熵越低（不纯度或者信息量越低）。
      • 比特or信息量也就是信息熵的单位。那么在谁是冠军的例子中每一个球队获胜的概率为1/32，通过折半计算的代价也就是信息熵为5：
      • 5 = - (1/32log1/32 + 1/32log1/32 + …),因为log1/32=-5（2**-5==1/32）为负数,所以求和后加一个负号表示正的结果5。5就是该事件的信息熵。
      • 如果获知了球队的往期获胜数据公开后，则德国获胜概率为1/4，西班牙为1/5，中国为1/20，则带入香农公式中为：
      • 5>=-(1/5log1/5 + 1/32log1/32 + 1/4log1/4+…) 结果值一定小于5
      • 结论：信息熵和消除不确定性是相关联的
        • 信息熵越大则表示信息的不确定性越大，猜对的代价大
        • 信息熵越小则表示信息的不确定性越小，猜对的代价小

信息增益

• 为什么越重要的特征要放在树的越靠上的节点位置呢？
  • 因为我们的分类结果是要从树的根节点开始自上而下的进行分步判断从而得到正确的划分结论。越重要的节点作为树中越靠上的节点可以减少基于该树进行分类的更多的不确定性。
    • 比如：将年龄作为根节点进行见面或者不见面的分类，可以比把收入作为根节点进行见或者不见的分类要降低了更多的不确定性。因为年龄如果太大的话直接就不见了，如果年龄适中则继续根据树下面的节点特征继续进行判断。如果将收入作为根节点，则收入高的话也不可以直接就见或者不见，还得考虑年纪问题，样貌问题等等。
  • 如何衡量决策树中节点（特征）的重要性呢？如何理解特征的重要性呢？
    • 重要性：如果一个节点减少分类的不确定性越明显，则该节点就越重要。
      • 年龄要比收入可以减少更多见与不见分类结果的不确定性。
    • 使用信息增益衡量特征的重要性
  • 信息增益
    • 在根据某个特征划分数据集之前之后信息熵发生的变化or差异叫做信息增益，知道如何计算信息增益，获得计算增益最高的特征就是最好的选择。
    • 信息增益作为决策树的划分依据，决定决策树怎么画，每个特征作为节点存放位置的确定。
    • 信息增益g(D,A)计算公式为：
    • $g(D,A)=H(D)-H(D|A)$
    • 公式解释：信息增益 = 划分前熵 - 划分后熵
    • 总之需要计算出每个特征的信息增益，特征的信息增益越大，则表示该特征越重要，应该放在决策树越靠上的位置！！！
• 构建决策树
  • 在构造决策树时，我们需要解决的第一个问题就是，当前数据集上哪个特征在划分数据分类时起决定性的作用。为了找到决定性的特征，划分出最好的结果，我们必须评估每个特征。那么在构造过程中，你要解决三个重要的问题：
    • 选择哪个属性作为根节点；
    • 选择哪些属性作为子节点；
    • 什么时候停止并得到目标状态，即叶节点。
  • 接下来以气象数据为例子，来说明决策树的构建过程：
    
    • 在没有使用特征划分类别的情况下，有9个yes和5个no，当前的熵为：
    • $H=-\sum _{i=1}^{n}p(x_i)lo{g}_{2}p(x_i)=-(\frac{5}{14}lo{g}_2\frac{5}{14}+\frac{9}{14}lo{g}_2\frac{9}{14})\approx 0.940$
    • 假设我们以 outlook 特征作为决策树的根节点划分数据集，对该特征每项指标分别统计：在不同的取值下 play 和 no play 的次数：
      
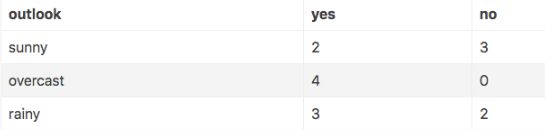
    • 此时各分支的熵计算如下：
    • $H(sunny)=-\sum _{i=1}^{n}p(x_i)lo{g}_{2}p(x_i)=-(\frac{2}{5}lo{g}_2\frac{2}{5}+\frac{3}{5}lo{g}_2\frac{3}{5})\approx 0.971$
    • $H(overcast)=-\sum _{i=1}^{n}p(x_i)lo{g}_{2}p(x_i)=-(lo{g}_{2}1)\approx 0$
    • $H(rainy)=-\sum _{i=1}^{n}p(x_i)lo{g}_{2}p(x_i)=-(\frac{3}{5}lo{g}_2\frac{3}{5}+\frac{2}{5}lo{g}_2\frac{2}{5})\approx 0.971$
    • — p(xi)指的是某一个节点（sunny）中，某一类别占据该节点总类别的比例
    • 因此如果用特征outlook来划分数据集的话，总的熵为：
      • 每一个outlook的组成的信息熵乘以outlook组成占总样本的比例
      • $H(outlook)=\frac{5}{14}\ast 0.971+\frac{4}{14}\ast 0+\frac{5}{14}\ast 0.971\approx 0.694$
    • 那么最终得到特征属性outlook带来的信息增益为：
      • g(outlook)=0.940−0.694=0.246
      • 然后用同样的方法，可以分别求出temperature，humidity，windy的信息增益分别为：
        • IG(temperature)=0.029
        • IG(humidity)=0.152
        • IG(windy)=0.048
        • 可以得出使用outlook特征所带来的信息增益最大。因此第一次切分过程将采用outlook字段进行切分数据集。
    • 第一次切分完毕后，分成了三个数据集sunny，overcast，rain。期中overcast所指向的数据集纯度为1，因此不用在对其进行切分。而剩下两个纯度不为1则需要对其继续切分。然而对sunny数据集而言使用humidity特征进行切分后节点纯度就变为1了，则不再进行继续切分，同理对rain而言使用windy特征进行切分纯度也变为了1不需要再次进行切分。最终决策树为如下：
      
• ID3的局限性
  • 不能直接处理连续型数据集(标签是连续型的)，若要使用ID3处理连续型变量，则首先需要对连续变量进行离散化
    • 连续性数据集是指数据的目标值为连续性，则无法计算某类别样例数量占总类别样例的占比。
  • 对缺失值较为敏感，使用ID3之前需要提前对缺失值进行处理
    • 存在缺失值则信息熵的公式无法计算结果
  • 没有剪枝的设置，容易导致过拟合，即在训练集上表现很好，测试集上表现很差
• 其他算法：
  • C4.5信息增益比
    • 分支度：在C4.5中，首先通过引入分支度的概念,来对信息增益的计算方法进行修正。而分支度的计算公式仍然是基于熵的算法，只是将信息熵计算公式中的p(xi)改成了p(vi)，p(vi)即某子节点的总样本数占父节点总样本数比例。这样的一个分支度指标，让我们在切分的时候，自动避免那些分类水平太多，信息熵减小过快的特征影响模型，减少过拟合情况。
    • 其中，i表示父节点的第i个子节点，vi表示第i个子节点样例数，P(vi)表示第i个子节点拥有样例数占父节点总样例数的比例。很明显，IV（Information Value）可作为惩罚项带入子节点的信息熵计算中。所以IV值会随着叶子节点上样本量的变小而逐渐变大，这就是说一个特征中如果标签分类太多（outlook特征的标签分类有rain，overcast，sunny）即使信息熵比较大，但是IV大的话，则信息熵除以IV后就会变小，每个叶子上的IV值就会非常大,树的分值就会越细。
    • $InformationValue=-\sum _{i=1}^{k}P(v_i)lo{g}_{2}P(v_i)$
    • 最终，在C4.5中，使用之前的信息增益除以分支度作为分支的参考指标，该指标被称作Gain Ratio(信息增益比)，计算公是为：
    • $GainRatio=\frac{InformationGain}{InformationValue}$
    • 增益比例是我们决定对哪一列进行分枝的标准，我们分枝的是数字最大的那一列，本质是信息增益最大，分支度又较小的列(也就是纯度提升很快，但又不是靠着把类别分特别细来提升的那些特征)。IV越大，即某一列的分类水平越 多，Gain ratio实现的惩罚比例越大。当然，我们还是希望GR越大越好
  • CART（基尼系数）
    • CART 的全称是分类与回归树。从这个名字中就应该知道，CART 既可以用于分类问题，也可以用于回归问题。
    • CART 与 ID3，C4.5 不同之处在于 CART 生成的树必须是二叉树。也就是说，无论是回归还是分类问题，无论特征是离散的还是连续的，无论属性取值有多个还是两个，内部节点只能根据属性值进行二分。
    • $Gini=1-\sum _{i=0}^{c-1}[p(i|t){]}^2$
• 如何选取使用何种算法?
  • 在实际使用中，信息熵和基尼系数的效果基本相同。信息熵的计算比基尼系数缓慢一些，因为基尼系数的计算不涉及对数。另外，因为信息熵对不纯度更加敏感，所以信息熵作为指标时，决策树的生长会更加“精细”，因此对于高维数据或者噪音很多的数据，信息熵很容易过拟合，基尼系数在这种情况下效果往往比较好。当模型拟合程度不足的时候，即当模型在训练集和测试集上都表 现不太好的时候，使用信息熵。当然，这些不是绝对的。
  • API:
  • class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, splitter=’best’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, class_weight=None, presort=False)[source]
• 创建一颗决策树
  • 使用datasets中的红酒数据集

from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier

wine = load_wine()
feature = wine.data
target = wine.target
x_train, x_test, y_train, y_test = train_test_split(feature, target, test_size=0.2, random_state=2021)
clf = DecisionTreeClassifier(criterion='entropy')
clf.fit(x_train, y_train)
print(clf.score(x_test, y_test))

• 为何每次测评的分数不一致呢？
  • 决策树在建树时，是靠优化节点来追求一棵最优化的树，但最优的节点能够保证构建出一颗最优的树吗?不能！sklearn表示，既然一棵树不能保证最优，那就建不同的树，然后从中取最好的。怎样从一组数据集中建不同的树呢?在每次分枝时，不使用全部特征，而是随机选取一部分特征，从中选取不纯度相关指标最优的作为分枝用的节点。这样，每次生成的树也就不同了。
• 参数random_state
  • random_state用来设置分枝中的随机模式的参数，默认None，在高维度时随机性会表现更明显，低维度的数据(比如鸢尾花数据集)，随机性几乎不会显现。输入任意整数，会一直长出同一棵树，让模型稳定下来

clf = DecisionTreeClassifier(criterion='entropy', random_state=2021)
clf.fit(x_train, y_train)
print(clf.score(x_test, y_test))

• 画决策树

from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier

wine = load_wine()
feature = wine.data
target = wine.target
x_train, x_test, y_train, y_test = train_test_split(feature, target, test_size=0.2, random_state=2021)
cl = DecisionTreeClassifier(criterion='entropy')
cl.fit(x_train, y_train)
print(cl.score(x_test, y_test))
clf = DecisionTreeClassifier(criterion='entropy', random_state=2021)
clf.fit(x_train, y_train)
print(clf.score(x_test, y_test))
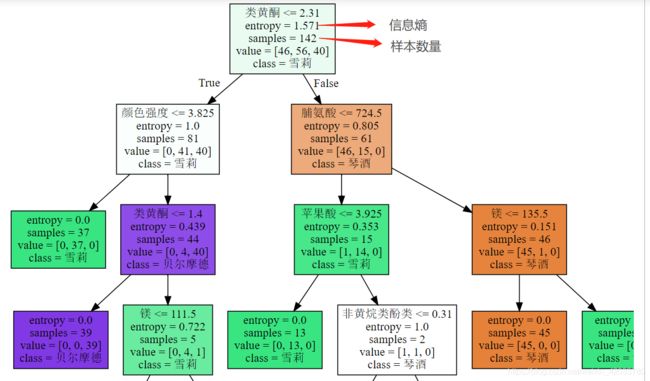
from sklearn import tree
import graphviz

feature_name = ['酒精', '苹果酸', '灰', '灰的碱性', '镁', '总酚', '类黄酮', '非黄烷类酚类', '花青素', '颜色强度', '色调', 'od280/od315稀释葡萄酒', '脯氨酸']
dot_data = tree.export_graphviz(clf,  # 训练好的决策树模型
                                out_file=None,  # 图片保存路径
                                feature_names=feature_name,  # 指定特征名称
                                class_names=["琴酒", "雪莉", "贝尔摩德"],  # 分类类别
                                filled=True  # 使用颜色分类结果
                                )
graph = graphviz.Source(dot_data)
print(graph)

注：需要安装graphviz图像界面软件

• 特征的重要属性
  • clf.feature_importances_ 返回特征的重要性 以后可以用决策树对特征进行选择

print(clf.feature_importances_)  # 返回特征的重要性\
featurea_name = ['酒精', '苹果酸', '灰', '灰的碱性', '镁', '总酚', '类黄酮', '非黄烷类酚类', '花青素', '颜 色强度', '色调', 'od280/od315稀释葡萄酒', '脯氨酸']
print([*zip(featurea_name, clf.feature_importances_)])

• 参数splitter
  • splitter也是用来控制决策树中的随机选项的，有两种输入值:
    • 输入”best"，决策树在分枝时虽然随机，但是还是会优先选择更重要的特征进行分枝(重要性可以通过属性feature_importances_查看)
    • 输入“random"，决策树在分枝时会更加随机，树会因为含有更多的不必要信息而更深更大，并因这些不必要信息而降低对训练集的拟合。这也是防止过拟合的一种方式。
    • 当你预测到你的模型会过拟合，用splitter和random_state这两个参数来帮助你降低树建成之后过拟合的可能性。

cll = DecisionTreeClassifier(criterion='entropy', random_state=2021, splitter='random')
cll.fit(x_train, y_train)
print(clf.score(x_test, y_test))

• 剪枝参数
  • 在不加限制的情况下，一棵决策树会生长到衡量不纯度的指标最优，或者没有更多的特征可用为止。这样的决策树 往往会过拟合，这就是说，它会在训练集上表现很好，在测试集上却表现糟糕。我们收集的样本数据不可能和整体 的状况完全一致，因此当一棵决策树对训练数据有了过于优秀的解释性，它找出的规则必然包含了训练样本中的噪 声，并使它对未知数据的拟合程度不足。
  • 为了让决策树有更好的泛化性，我们要对决策树进行剪枝。剪枝策略对决策树的影响巨大，正确的剪枝策略是优化 决策树算法的核心。sklearn为我们提供了不同的剪枝策略:
    • max_depth：限制树的最大深度，超过设定深度的树枝全部剪掉
      • 这是用得最广泛的剪枝参数，在高维度低样本量时非常有效。决策树多生长一层，对样本量的需求会增加一倍，所以限制树深度能够有效地限制过拟合。在集成算法中也非常实用。实际使用时，建议从=3开始尝试，看看拟合的效果再决定是否增加设定深度。
    • min_samples_leaf & min_samples_split：
      • min_samples_leaf限定，一个节点在分枝后的每个子节点都必须包含至少min_samples_leaf个训练样本，否则分 枝就不会发生，或者，分枝会朝着满足每个子节点都包含min_samples_leaf个样本的方向去发生。一般搭配max_depth使用。这个参数的数量设置得太小会引 起过拟合，设置得太大就会阻止模型学习数据。一般来说，建议从=5开始使用。
      • min_samples_split限定，一个节点必须要包含至少min_samples_split个训练样本，这个节点才允许被分枝，否则分枝就不会发生。

import graphviz
from sklearn.tree import DecisionTreeClassifier

clf1 = DecisionTreeClassifier(criterion='entropy', random_state=2021, max_depth=4  # 树最多只能4层，超过就会剪掉，不算根节点
                              , min_samples_leaf=10,  # 一个节点分支后每个叶子必须最少有10个样本，否则不分枝
                              min_samples_split=20  # 节点必须有20个样本才允许分支，否则就不能分枝
                              )
clf1.fit(x_train, y_train)
dot_datat = tree.export_graphviz(clf1, feature_names=feature_name, class_names=["琴酒", "雪莉", "贝尔摩德"], filled=True,
                                 out_file=None)
grapht = graphviz.Source(dot_datat)
print(grapht)

• 案例应用、泰坦尼克号乘客生存分类
  • 泰坦尼克号的沉没是世界上最严重的海难事故之一，今天我们通过分类树模型来预测一下哪些人可能成为幸存者。
  • 特征介绍
    Survived：是否生存
    Pclass：船票等级，表示乘客社会经济地位
    Name，Sex，Age
    SibSp：泰坦尼克号上的兄弟姐妹/配偶数
    Parch：泰坦尼克号上的父母/子女数量
    Ticket：船票号
    Fare：票价
    Cabin：船舱号
    Embarked：登船港口号

import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split

data = pd.read_csv("titanic.csv", index_col='PassengerId')
print(data.head())
print(data.info())
# 删除缺失值较多和无关的特征
data.drop(labels=['Cabin', 'Name', 'Ticket'], inplace=True, axis=1)
# 填充age列
data["Age"] = data["Age"].fillna(data["Age"].mean())
#  清洗空值
data.dropna(inplace=True)
print(data.head())
# 将性别转换成数值型数据
data['Sex'] = (data['Sex'] == 'male').astype("int")
print(data.head())
# 将三分类变量转换为数值型变量
labels = data['Embarked'].unique().tolist()
data['Embarked'] = data['Embarked'].map(lambda x: labels.index(x))
x = data.iloc[:, data.columns != 'Survived']
y = data.iloc[:, data.columns == 'Survived']
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=2021)
clf = DecisionTreeClassifier(criterion='gini', max_depth=7, min_samples_leaf=11, splitter='best', random_state=25)
clf.fit(x_train, y_train)
print(clf.score(x_test, y_test))

• 用网格搜索调整参数
  • Grid Search：一种调参手段；穷举搜索：在所有候选的参数选择中，通过循环遍历，尝试每一种可能性，表现最好的参数就是最终的结果。其原理就像是在数组里找最大值。（为什么叫网格搜索？以有两个参数的模型为例，参数a有3种可能，参数b有4种可能，把所有可能性列出来，可以表示成一个3*4的表格，其中每个cell就是一个网格，循环过程就像是在每个网格里遍历、搜索，所以叫grid search）

from sklearn.model_selection import GridSearchCV

parameters = {'splitter': ('best', 'random'), 'criterion': ('gini', 'entropy'), 'max_depth': [*range(1, 10)],
              'min_samples_leaf': [*range(1, 50, 5)]
              }
GS = GridSearchCV(clf, parameters, cv=10)  # cv交叉验证
GS.fit(x_train, y_train)
print(GS.best_params_)
# print(GS.best_estimator_)
print(GS.best_score_)

集成学习

• 集成学习(ensemble learning)是时下非常流行的机器学习算法，它本身不是一个单独的机器学习算法，而是通过在数据上构建多个模型，集成所有模型的建模结果。
• 集成算法的目标
  • 集成算法会考虑多个评估器的建模结果，汇总之后得到一个综合的结果，以此来获取比单个模型更好的回归或分类表现。
• 或者说在机器学习的众多算法中，我们的目标是学习出一个稳定的且在各个方面表现都较好的模型，但实际情况往往不这么理想，有时我们只能得到多个有偏好的模型（弱监督模型（弱评估器，基评估器），在某些方面表现的比较好）。集成学习就是组合这里的多个弱监督模型一起得到一个更好更全面的强监督模型。（三个臭皮匠赛过诸葛亮）
  • 集成学习潜在的思想是即便某一个弱评估器得到了错误的预测，其他的弱评估器也可以将错误纠正回来。
• 集成学习就是将多个弱学习器集合成一个强学习器，你可以理解成现在有一些判断题（判断对错即01），如果让学霸去做这些题，可能没啥问题，几乎全部都能做对，但是现实情况是学霸不常有，学渣倒是很多，学渣做题怎么样做才能保证题做对的准确率较高呢？就是让多个学渣一起做， 每个人随机挑选一部分题目来做（每人挑的题目会有重复的），最后将所有人的结果进行汇总，然后进行投票根据将票多者作为最后的结果；另一种方式就是先让学渣A做一遍，然后再让学渣B做，且让B重点关注A做错的那些题，再让C做，同样重点关注B做错的，依次循环，直到所有的学渣都把题目做了一遍为止。通过上面两种方式就可以做到学渣也能取得和学霸一样的成绩啦。我们把这种若干个学渣组合达到学霸效果的这种方式称为集成学习。
• 实现集成学习的方法可以分为两类：
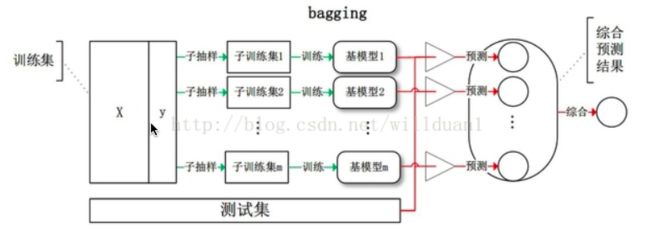
  • 并行集成方法（装袋法Bagging）：
    • 其中参与训练的基础学习器并行生成（例如 Random Forest）。并行方法的原理是利用基础学习器之间的独立性，通过平均或者投票的方式可以显著降低错误。
    • 多个学渣一起做， 每个人随机挑选一部分题目来做，最后将所有人的结果进行汇总，然后根据将票多者作为最后的结果
    • 序列集成方法（提升法Boosting）：
      • 其中参与训练的基础学习器按照顺序生成（例如 AdaBoost）。序列方法的原理是利用基础学习器之间的依赖关系。通过对之前训练中错误标记的样本赋值较高的权重，可以提高整体的预测效果。
      • 先让学渣A做一遍，然后再让学渣B做，且让B重点关注A做错的那些题，再让C做，同样重点关注B做错的，依次循环，直到所有的学渣都把题目做了一遍为止
        
  • 实现集成学习的方法有：
    • Bagging
    • Boosting
    • Stacking
• 实现集成学习的算法
• Bagging装袋法
  • 全称为bootstrap aggregating。它是一种有放回的抽样方法，其算法过程如下：
    • 从原始样本集中抽取训练集。每轮从原始样本集中使用有放回的方法抽取n个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）。共进行k轮抽取，得到k个训练集。（k个训练集之间是相互独立的）
    • 每次使用一个训练集得到一个模型，k个训练集共得到k个模型。（注：这里并没有具体的分类算法或回归方法，我们可以根据具体问题采用不同的分类或回归方法，如决策树、感知器等）
    • 对分类问题：将上步得到的k个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。（所有模型的重要性相同）
      
• Boosting提升法
  • 其主要思想是将弱学习器组装成一个强学习器。
  • 关于Boosting的核心思想：
    • 通过提高那些在前一轮被弱分类器分错样例的权值，减小前一轮分对样例的权值（使得弱分类器可以对分错样例更敏感），来使得分类器对误分的数据有较好的效果。
    • 也就是说算法刚开始训练时对每一个训练样本赋相等的权重，然后用该算法对训练集训练t轮，每次训练后，对训练失败的训练例赋以较大的权重，也就是让学习算法在每次学习以后更注意学错的样本。
      
• Stacking
  • Stacking方法是指训练一个模型用于组合其他各个模型。首先我们先训练多个不同的模型，然后把之前训练的各个模型的输出为输入来训练一个模型，以得到一个最终的输出。
  • 如下图，先在整个训练数据集上通过有放回抽样得到各个训练集合，得到一系列分类模型，然后将输出用于训练第二层分类器。
    
• Bagging，Boosting二者之间的区别
  • 样本选择上：
    • Bagging：训练集是在原始集中有放回选取的，从原始集中选出的各轮训练集之间是独立的。
    • Boosting：每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。
  • 样例权重：
    • Bagging：使用均匀取样，每个样例的权重相等
    • Boosting：根据错误率不断调整样例的权值，错误率越大则权重越大。

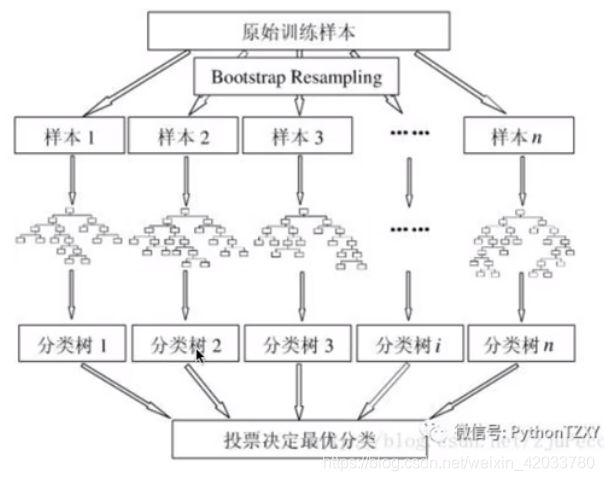
随机森林：是bagging装袋法的代表。弱学习器只可以是决策树

• 简介：

  • 随机森林是一种有监督学习算法，是以决策树为基学习器的集成学习算法。随机森林非常简单，易于实现，计算开销也很小，在分类和回归上表现出非常惊人的性能，因此，随机森林被誉为“代表集成学习技术水平的方法”。

  • 随机森林的随机性体现在哪几个方面呢？

    • **1.数据集的随机选择 **
      • 从原始数据集中采取《有放回的抽样bagging》，构造子数据集。不同子数据集的元素可以重复，同一个子数据集中的元素也可以重复。
    • 2.待选特征的随机选取
      • 随机森林中的子树的每一个分裂过程并未用到所有的待选特征，而是从所有的待选特征中随机选取一定的特征，之后再随机选取的特征中选取最优的特征。

  • 随机森林的重要作用：

    • 可以用于分类问题，也可以用于回归问题
    • 可以解决模型过拟合的问题，对于随机森林来说，如果随机森林中的树足够多，那么分类器就不会出现过拟合
    • 可以检测出特征的重要性，从而选取好的特征

  • 随机森林的构建过程

    • 1.从原始训练集中随机有放回采样取出m个样本,生成m个训练集
    • 2.对m个训练集，我们分别训练m个决策树模型
    • 3.对于单个决策树模型，假设训练样本特征的个数为n，那么每次分裂时根据信息增益/信息增益比/基尼指数 选择最好的特征进行分裂
    • 4.将生成的多颗决策树组成随机森林。对于分类问题，按照多棵树分类器投票决定最终分类结果；对于回归问题，由多颗树预测值的均值决定最终预测结果
      

  • 优点：
    1.由于采用了集成算法，本身精度比大多数单个算法要好，所以准确性高
    2.由于两个随机性的引入，使得随机森林不容易陷入过拟合（样本随机，特征随机）
    3.在工业上，由于两个随机性的引入，使得随机森林具有一定的抗噪声能力，对比其他算法具有一定优势
    4.它能够处理很高维度（feature很多）的数据，并且不用做特征选择，对数据集的适应能力强：既能处理离散型数据，也能处理连续型数据
    5.在训练过程中，能够检测到feature间的互相影响，且可以得出feature的重要性，具有一定参考意义

  • 缺点：
    1.当随机森林中的决策树个数很多时，训练时需要的空间和时间会比较大

  • 在sklearn.ensemble库中，我们可以找到Random Forest分类和回归的实现：
    API：from sklearn.ensemble import RandomForestClassifier,RandomForestRegressor
    RandomForestClassifier # 分类
    RandomForestRegression # 回归

• 控制弱评估器 (随机森林为决策树) 的参数
  
• n_estimators（指定弱评估器数）
  • 这是森林中树木的数量，即基评估器的数量。这个参数对随机森林模型的精确性影响是单调的，n_estimators越大，模型的效果往往越好。但是相应的，任何模型都有决策边界，n_estimators达到一定的程度之后，随机森林的 精确性往往不再上升或开始波动，并且，n_estimators越大，需要的计算量和内存也越大，训练的时间也会越来越 长。对于这个参数，我们是渴望在训练难度和模型效果之间取得平衡。
  • n_estimators的默认值在现有版本的sklearn中是10，但是在即将更新的0.22版本中，这个默认值会被修正为 100。这个修正显示出了使用者的调参倾向:要更大的n_estimators。
• 分类随机森林RandomForestClassifier
  • 树模型的优点是简单易懂，可视化之后的树人人都能够看懂，可惜随机森林是无法被可视化的。所以为了更加直观地让大家体会随机森林的效果，我们来进行一个随机森林和单个决策树效益的对比。我们依然使用红酒数据集

from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.metrics import f1_score
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression

x = load_wine().data
y = load_wine().target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=2021)
# 逻辑回归
l = LogisticRegression(solver='liblinear').fit(x_train, y_train)  # solver为求解器
print(f1_score(y_test, l.predict(x_test), average='micro'))
# 决策树
d = DecisionTreeClassifier().fit(x_train, y_train)
print(f1_score(y_test, d.predict(x_test), average='micro'))
# 随机森林
r = RandomForestClassifier().fit(x_train, y_train)
print(f1_score(y_test, r.predict(x_test), average='micro'))

• 画出随机森林和决策树在一组交叉验证下的效果对比

from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt

rfc = RandomForestClassifier(n_estimators=25)
rfc_s = cross_val_score(rfc,wine.data,wine.target,cv=10)
clf = DecisionTreeClassifier()
clf_s = cross_val_score(clf,wine.data,wine.target,cv=10)
plt.plot(range(1,11),rfc_s,label = "RandomForest")
plt.plot(range(1,11),clf_s,label = "Decision Tree")
plt.legend()
plt.show()

• 画出随机森林和决策树在十组交叉验证下的效果对比

rfc_l = []
clf_l = []
for i in range(10):
    rfc = RandomForestClassifier(n_estimators=25)
    rfc_s = cross_val_score(rfc, x, y, cv=10).mean()
    rfc_l.append(rfc_s)
    clf = DecisionTreeClassifier()
    clf_s = cross_val_score(clf, x, y, cv=10).mean()
    clf_l.append(clf_s)
plt.plot(range(1, 11), rfc_l, label="RandomForest")
plt.plot(range(1, 11), clf_l, label="DecisionTree")
plt.legend()
plt.show()

• 随机森林重要参数
  • random_state
    • 随机森林中的random_state控制的是生成森林的模式，类似决策树中的random_state，用来固定森林中树的随机性。当random_state固定时，随机森林中生成是一组固定的树。否则每次产生的树会不一样
  • bootstrap & oob_score
    • bootstrap (有放回抽样)：
      • 装袋法是通过有放回的随机抽样技术来形成不同的训练数据，bootstrap就是用来控制抽样技术的参数。我们进行样本的随机采样，每次采样一个样本，并在抽取下一个样本之前将该样本 放回原始训练集，也就是说下次采样时这个样本依然可能被采集到。bootstrap参数默认True，代表采用这种有放回的随机抽样技术。通常，这个参数不会被我们设置为False。
    • oob_score (袋外数据做测试)：
      • 然而有放回抽样也会有自己的问题。由于是有放回，一些样本可能会被采集多次，而其他一些样本却可能被忽略，一次都未被采集到。那么这些被忽略或者一次都没被采集到的样本叫做oob袋外数据。
    • 也就是说，在使用随机森林时，我们可以不划分测试集和训练集，只需要用袋外数据来测试我们的模型即可。如果希望用袋外数据来测试，则需要在实例化时就将oob_score这个参数调整为True，训练完毕之后，我们可以用随机森林的另一个重要属性:oob_score_来查看我们的在袋外数据上测试的结果:

# 无需划分训练集和测试集
rfc = RandomForestClassifier(n_estimators=25, oob_score=True)
rfc = rfc.fit(x, y)
print(rfc.oob_score_)

• 回归随机森林RandomForestRegressor
  • 所有的参数，属性与接口，全部和随机森林分类器一致。仅有的不同就是回归树与分类树的不同，不纯度的指标， 参数Criterion不一致。
  • Criterion参数：
    • 回归树衡量分枝质量的指标，支持的标准有三种：
      • 输入"mse"使用均方误差mean squared error(MSE)，父节点和叶子节点之间的均方误差的差额将被用来作为特征选择的标准，这种方法通过使用叶子节点的均值来最小化L2损失
      • 输入“friedman_mse”使用费尔德曼均方误差，这种指标使用弗里德曼针对潜在分枝中的问题改进后的均方误差
      • 输入"mae"使用绝对平均误差MAE(mean absolute error)，这种指标使用叶节点的中值来最小化L1损失

from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston

x = load_boston().data
y = load_boston().target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=2021)
d = DecisionTreeRegressor(criterion='friedman_mse').fit(x_train, y_train)
print(d.score(x_test, y_test))

r = RandomForestRegressor(criterion='friedman_mse').fit(x_train, y_train)
print(r.score(x_test, y_test))

• 进行又放回的随机抽样时，每一个弱评估器使用的训练数据和原始样本的训练数据量级一致

xgboost

• xgboost介绍
  • XGBoost全称是eXtreme Gradient Boosting，可译为极限梯度提升算法。它由陈天奇所设计，致力于让提升树突破自身的计算极限，以实现运算快速，性能优秀的工程目标。和传统的梯度提升算法相比，XGBoost进行了许多改进，并且已经被认为是在分类和回归上都拥有超高性能的先进评估器。 在各平台的比赛中、高科技行业和数据咨询等行业也已经开始逐步使用XGBoost，了解这个算法，已经成为学习机器学习中必要的一环。
  • 性能超强的算法往往有着复杂的原理，XGBoost也不能免俗，因此它背后的数学深奥复杂。
• xgboost库与XGB的sklearn API
  • 在开始讲解XGBoost的细节之前，我先来介绍我们可以调用XGB的一系列库，模块和类。陈天奇创造了XGBoost之后，很快和一群机器学习爱好者建立了专门调用XGBoost库，名为xgboost。xgboost是一个独立的，开源的，专门提供XGBoost算法应用的算法库。它和sklearn类似，有一个详细的官方网站可以供我们查看，并且可以与C，Python，R，Julia等语言连用，但需要我们单独安装和下载。
    • xgboostdocuments:xgboostdocuments
• 我们有两种方式可以来使用我们的xgboost库
  • 第一种方式：是直接使用xgboost库自己的建模流程
    
  • 其中最核心的，是DMtarix这个读取数据的类，以及train()这个用于训练的类。与sklearn把所有的参数都写在类中的方式不同，xgboost库中必须先使用字典设定参数集，再使用train来将参数及输入，然后进行训练。会这样设计的原因，是因为XGB所涉及到的参数实在太多，全部写在xgb.train()中太长也容易出错。在这里，我为大家准备了 params可能的取值以及xgboost.train的列表，给大家一个印象。
    
• 第二种方式：使用XGB库中的sklearn的API
  • 我们可以调用如下的类，并用我们sklearn当中惯例的实例化，fit和predict的流程来运行XGB，并且也可以调用属性比如coef_等等。当然，这是我们回归的类，我们也有用于分类的类。他们与回归的类非常相似，因此了解一个类即可。
    
  • 看到这长长的参数列表，可能大家会感到头晕眼花——没错XGB就是这么的复杂。但是眼尖的小伙伴可能已经发现了， 调用xgboost.train和调用sklearnAPI中的类XGBRegressor，需要输入的参数是不同的，而且看起来相当的不同。但其实，这些参数只是写法不同，功能是相同的。
    • 比如说，我们的params字典中的第一个参数eta，其实就是我们XGBRegressor里面的参数learning_rate，他们的含义和实现的功能是一模一样的。只不过在sklearnAPI中，开发团队友好地帮助我们将参数的名称调节成了与sklearn中其他的算法类更相似的样子。
  • 两种使用方式的区别：
    • 使用xgboost中设定的建模流程来建模，和使用sklearnAPI中的类来建模，模型效果是比较相似的，但是xgboost库本身的运算速度(尤其是交叉验证)以及调参手段比sklearn要简单。
    • 但是，我们前期已经习惯使用sklearn的调用方式，我们就先使用sklearn的API形式来讲解和使用XGB。
• 梯度提升算法：XGBoost的基础是梯度提升算法，因此我们必须先从了解梯度提升算法开始。
  • 梯度提升(Gradient boosting)：
    • 是构建预测模型的最强大技术之一，它是集成算法中提升法(Boosting)的代表算法。集成算法通过在数据上构建多个弱评估器，汇总所有弱评估器的建模结果，以获取比单个模型更好的回归或分类表现。
      • 集成不同弱评估器的方法有很多种。就像我们曾经在随机森林的课中介绍的，一次性建立多个平行独立的弱评估器的装袋法。也有像我们今天要介绍的提升法这样，逐一构建弱评估器，经过多次迭代逐渐累积多个弱评估器的方法。
    • 我们知道梯度提升法是集成算法中提升法(Boosting)的代表算法。回顾：在集成学习讲解中我们说boosting算法是将其中参与训练的基础学习器按照顺序生成。序列方法的原理是利用基础学习器之间的依赖关系。通过对之前训练中错误标记的样本赋值较高的权重，可以提高整体的预测效果。
      • 基于梯度提升的回归或分类模型来讲，其建模过程大致如下:最开始先建立一棵树，然后逐渐迭代，每次迭代过程中都增加一棵树，逐渐形成众多树模型集成的强评估器。
        
  • XGB算法原理：
    • XGB中构建的弱学习器为CART树，这意味着XGBoost中所有的树都是二叉的。
      • 在讲解决策树算法原理时，我们主要讲解的是信息熵实现的树模型，除此外，还有一种是基于基尼系数实现的CART树，它既可以处理分类也可以处理回归问题，并且构建出的只能是二叉树。
    • XGBT中的预测值是所有弱分类器上的叶子节点权重直接求和得到，计算叶子权重是一个复杂的过程。
    • 那么什么是叶子的权重呢？
      • 先来举个例子，我们要预测一家人对电子游戏的喜好程度，考虑到年轻和年老相比，年轻更可能喜欢电子游戏，以及男性和女性相比，男性更喜欢电子游戏，故先根据年龄大小区分小孩和大人，然后再通过性别区分开是男是女，逐一给各人在电子游戏喜好程度上打分，这个分值就是叶子节点的权重。假设，我们训练出了2棵树tree1和tree2，两棵树的结论的打分值累加起来便是最终的结论，所以小男孩的预测分数就是两棵树中小男孩所落到的结点的分数相加：2 + 0.9 = 2.9。爷爷的预测分数同理：-1 + （-0.9）= -1.9。具体如下图所示：：
        
  • 因此，假设这个集成模型XGB中总共有k棵决策树，则整个模型在这个样本i上给出的预测结果为:
    
    • yi(k)表示k课树叶子节点权重的累和或者XGB模型返回的预测结果，K表示树的总和，fk(xi)表示第k颗决策树返回的叶子节点的权重（第k棵树返回的结果）
  • 从上面的式子来看，在集成中我们需要的考虑的第一件事是我们的超参数K，究竟要建多少棵树呢?
    • 试着回想一下我们在随机森林中是如何理解n_estimators的:n_estimators越大，模型的学习能力就会越强，模型也 越容易过拟合。在随机森林中，我们调整的第一个参数就是n_estimators，这个参数非常强大，常常能够一次性将模 型调整到极限。在XGB中，我们也期待相似的表现，虽然XGB的集成方式与随机森林不同，但使用更多的弱分类器来 增强模型整体的学习能力这件事是一致的。

from xgboost import XGBRegressor as xgbr
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.datasets import load_boston
from sklearn.metrics import mean_squared_error as MSE
from sklearn.model_selection import KFold, cross_val_score, train_test_split

data = load_boston()
x = data.data
y = data.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=420)
# xgb
reg = xgbr(n_estimators=100).fit(x_train, y_train)
print(reg.score(x_test, y_test))
print(MSE(y_test, reg.predict(x_test)))
print(cross_val_score(reg, x_train, y_train, cv=5).mean())
# 随机森林
rfr = RFR(n_estimators=100).fit(x_train, y_train)
print(rfr.score(x_test, y_test))
print(MSE(y_test, rfr.predict((x_test))))
print(cross_val_score(rfr, x_train, y_train, cv=5).mean())
model_count = []
scores = []
for i in range(50, 170):
    xgb = xgbr(n_estimators=i).fit(x_train, y_train)
    score = xgb.score(x_test, y_test)
    scores.append(score)
    model_count.append(i)
import matplotlib.pyplot as plt

plt.plot(model_count, scores)
plt.show()

• 重要参数
• 有放回随机抽样:subsample(0-1,默认为1)
  • 确认了有多少棵树之后，我们来思考一个问题:建立了众多的树，怎么就能够保证模型整体的效果变强呢?集成的目的是为了模型在样本上能表现出更好的效果，所以对于所有的提升集成算法，每构建一个评估器，集成模型的效果都会比之前更好。也就是随着迭代的进行，模型整体的效果必须要逐渐提升，最后要实现集成模型的效果最优。要实现这个目标，我们可以首先从训练数据上着手。
  • 我们训练模型之前，必然会有一个巨大的数据集。我们都知道树模型是天生容易发生过拟合，并且如果数据量太过巨 大，树模型的计算会非常缓慢，因此，我们要对我们的原始数据集进行有放回抽样(bootstrap)。有放回的抽样每 次只能抽取一个样本，若我们需要总共N个样本，就需要抽取N次。每次抽取一个样本的过程是独立的，这一次被抽到的样本会被放回数据集中，下一次还可能被抽到，因此抽出的数据集中，可能有一些重复的数据。
  • 在无论是装袋还是提升的集成算法中，有放回抽样都是我们防止过拟合，让单一弱分类器变得更轻量的必要操作。实际应用中，每次抽取50%左右的数据就能够有不错的效果了。sklearn的随机森林类中也有名为boostrap的参数来帮 助我们控制这种随机有放回抽样。
  • 在梯度提升树中，我们每一次迭代都要建立一棵新的树，因此我们每次迭代中，都要有放回抽取一个新的训练样本。不过，这并不能保证每次建新树后，集成的效果都比之前要好。因此我们规定，在梯度提升树中，每构建一个评估器，都让模型更加集中于数据集中容易被判错的那些样本。
  • 首先我们有一个巨大的数据集，在建第一棵树时，我们对数据进行初次又放回抽样，然后建模。建模完毕后，我们对模型进行一个评估，然后将模型预测错误的样本反馈给我们的数据集，一次迭代就算完成。紧接着，我们要建立第二棵决策树，于是开始进行第二次又放回抽样。但这次有放回抽样，和初次的随机有放回抽样就不同了，在这次的抽样中，我们加大了被第一棵树判断错误的样本的权重。也就是说，被第一棵树判断错误的样本，更有可能被我们抽中。
  • 基于这个有权重的训练集来建模，我们新建的决策树就会更加倾向于这些权重更大的，很容易被判错的样本。建模完毕之后，我们又将判错的样本反馈给原始数据集。下一次迭代的时候，被判错的样本的权重会更大，新的模型会更加倾向于很难被判断的这些样本。如此反复迭代，越后面建的树，越是之前的树们判错样本上的专家，越专注于攻克那些之前的树们不擅长的数据。对于一个样本而言，它被预测错误的次数越多，被加大权重的次数也就越多。我们相信，只要弱分类器足够强大，随着模型整体不断在被判错的样本上发力，这些样本会渐渐被判断正确。如此就一定程度上实现了我们每新建一棵树模型的效果都会提升的目标。
  • 在sklearn中，我们使用参数subsample来控制我们的随机抽样。在xgb和sklearn中，这个参数都默认为1且不能取到 0，这说明我们无法控制模型是否进行随机有放回抽样，只能控制抽样抽出来的样本量大概是多少。
  • 注意：那除了让模型更加集中于那些困难错误样本，采样还对模型造成了什么样的影响呢?采样会减少样本数量，而从学习曲线来看样本数量越少模型的过拟合会越严重，因为对模型来说，数据量越少模型学习越容易，学到的规则也会越具体越不适用于测试样本。所以subsample参数通常是在样本量本身很大的时候来调整和使用。

import numpy as np

subs = []
scores = []
for i in np.linspace(0.05, 1, 20):
    xgb = xgbr(n_estimators=182, subsample=i).fit(x_train, y_train)
    score = xgb.score(x_test, y_test)
    subs.append(i)
    scores.append(score)
plt.plot(subs, scores)
plt.show()

• 迭代的速率:learning_rate
  • 从数据的角度而言，我们让模型更加倾向于努力攻克那些难以判断的样本。但是，并不是说只要我新建了一棵倾向于困难样本的决策树，它就能够帮我把困难样本判断正确了。困难样本被加重权重是因为前面的树没能把它判断正确，所以对于下一棵树来说，它要判断的测试集的难度，是比之前的树所遇到的数据的难度都要高的，那要把这些样本都判断正确，会越来越难。如果新建的树在判断困难样本这件事上还没有前面的树做得好呢?如果我新建的树刚好是一棵特别糟糕的树呢?所以，除了保证模型逐渐倾向于困难样本的方向，我们还必须控制新弱分类器的生成，我们必须保证，每次新添加的树一定得是对这个新数据集预测效果最优的那一棵树
  • 思考：如何保证每次新添加的树一定让集成学习的效果提升呢？
    • 现在我们希望求解集成算法的最优结果，那我们可以:我们首先找到一个损失函数obj，这个损失函数应该可以通过带入我们的预测结果y来衡量我们的梯度提升树在样本的预测效果。然后，我们利用梯度下降来迭代我们的集成算法。
    • 在模型中，使用参数learning_rate来表示迭代的速率。learning_rate值越大表示迭代速度越快，算法的极限会很快被达到，有可能无法收敛到真正最佳的损失值。learning_rate越小就越有可能找到更加精确的最佳值，但是迭代速度会变慢，耗费更多的运算空间和成本。

rates = []
scoresr = []
for i in np.linspace(0.05, 1, 20):
    xgb = xgbr(n_estimators=182, subsample=0.9, learning_rate=i).fit(x_train, y_train)
    scorer = xgb.score(x_test, y_test)
    rates.append(i)
    scoresr.append(scorer)
plt.plot(rates, scoresr)
plt.show()

• 选择弱评估器：booster
  • 梯度提升算法中不只有梯度提升树，XGB作为梯度提升算法的进化，自然也不只有树模型一种弱评估器。在XGB中， 除了树模型，我们还可以选用线性模型，比如线性回归，来进行集成。虽然主流的XGB依然是树模型，但我们也可以 使用其他的模型。基于XGB的这种性质，我们有参数“booster"来控制我们究竟使用怎样的弱评估器。
    

for booster in ["gbtree", "gblinear", "dart"]:
    reg = xgbr(n_estimators=180, learning_rate=0.1, random_state=420, booster=booster).fit(x_train, y_train)
    print(booster)
    print(reg.score(x_test, y_test))

无监督学习与聚类算法

• 概述
  • 在此之前我们所学习到的算法模型都是属于有监督学习的模型算法，即模型需要的样本数据既需要有特征矩阵X，也需要有真实的标签y。那么在机器学习中也有一部分的算法模型是属于无监督学习分类的，所谓的无监督学习是指模型只需要使用特征矩阵X即可，不需要真实的标签y。那么聚类算法就是无监督学习中的代表之一。
• 聚类算法
  • 聚类算法其目的是将数据划分成有意义或有用的组(或簇)。这种划分可以基于我们的业务 需求或建模需求来完成，也可以单纯地帮助我们探索数据的自然结构和分布。比如在商业中，如果我们手头有大量 的当前和潜在客户的信息，我们可以使用聚类将客户划分为若干组，以便进一步分析和开展营销活动。
  • **聚类和分类区别 **
    
    
• KMeans算法原理阐述
  • 簇与质心
    • 簇：KMeans算法将一组N个样本的特征矩阵X划分为K个无交集的簇，直观上来看是簇是一个又一个聚集在一起的数 据，在一个簇中的数据就认为是同一类。簇就是聚类的结果表现。
    • 质心：簇中所有数据的均值u通常被称为这个簇的“质心”(centroids)。
      • 在一个二维平面中，一簇数据点的质心的横坐标就是这一簇数据点的横坐标的均值，质心的纵坐标就是这一簇数据点的纵坐标的均值。同理可推广至高维空间。
      • 质心的个数也聚类后的类别数是一致的
  • 在KMeans算法中，簇的个数K是一个超参数，需要我们人为输入来确定。KMeans的核心任务就是根据我们设定好的K，找出K个最优的质心，并将离这些质心最近的数据分别分配到这些质心代表的簇中去。具体过程可以总结如下:
    
    • 那什么情况下，质心的位置会不再变化呢?当我们找到一个质心，在每次迭代中被分配到这个质心上的样本都是一致的，即每次新生成的簇都是一致的，所有的样本点都不会再从一个簇转移到另一个簇，质心就不会变化了。
    • 这个过程在可以由下图来显示，我们规定，将数据分为4簇(K=4)，其中白色X代表质心的位置:
      
• 聚类算法聚出的类有什么含义呢?这些类有什么样的性质?
  • 我们认为，被分在同一个簇中的数据是有相似性的，而不同簇中的数据是不同的，当聚类完毕之后，我们就要分别去研究每个簇中的样本都有什么样的性质，从而根据业务需求制定不同的商业或者科技策略。
  • 聚类算法追求“簇内差异小，簇外差异大”：
    • 而这个“差异“，由样本点到其所在簇的质心的距离来衡量。
    • 对于一个簇来说，所有样本点到质心的距离之和越小，我们就认为这个簇中的样本越相似，簇内差异就越小。而距离的衡量方法有多种，令x表示簇中的一个样本点，u表示该簇中的质心，n表示每个样本点中的特征数目，i表示组成点的每个特征，则该样本点到质心的距离可以由以下距离来度量:
    • $欧几里得距离：d(x,\mu )=\sqrt{\sum _{i=1}^n(x_i-{\mu }_i{)}^2}$
    • $曼哈顿距离：d(x,\mu )=\sum _{i=1}^n|(x_i-\mu )|$
    • $余弦距离：\cos \theta =\frac{{\sum }_1^n(x_i\ast \mu )}{\sqrt{{\sum }_1^n(x_i{)}^2}\ast \sqrt{{\sum }_1^n(\mu {)}^2}}$
  • KMeans有损失函数吗？
    • 簇内平方和
      • 如我们采用欧几里得距离，则一个簇中所有样本点到质心的距离的平方和为簇内平方和。使用簇内平方和就可以表示簇内差异的大小
    • 整体平方和
      • 将一个数据集中的所有簇的簇内平方和相加，就得到了整体平方和(Total Cluster Sum of Square)，又叫做total inertia。Total Inertia越小，代表着每个簇内样本越相似，聚类的效果就越好。
      • KMeans追求的是，求解能够让簇内平方和最小化的质心。实际上，在质心不断变化不断迭代的过程中，整体平方和是越来越小的。我们可以使用数学来证明，当整体平方和最小的时候，质心就不再发生变化了。如此，K-Means的求解过程，就变成了一个最优化问题。因此我们认为：
        • 在KMeans中，我们在一个固定的簇数K下，最小化整体平方和来求解最佳质心，并基于质心的存在去进行聚类。并且，整体距离平方和的最小值其实可以使用梯度下降来求解。因此，有许多博客和教材都这样写道:簇内平方和/整体平方和是KMeans的损失函数。
      • 但是也有人认为：
        • 损失函数本质是用来衡量模型的拟合效果的（损失越小，模型的拟合效果越好），只有有着求解参数需求的算法，才会有损失函数。Kmeans不求解什么参数，它的模型本质也没有在拟合数据，而是在对数据进行一种探索。所以如果你去问大多数数据挖掘工程师，甚至是算法工程师，他们可能会告诉你说，K-Means不存在 什么损失函数，整体平方和更像是Kmeans的模型评估指标，而非损失函数。
      • API：sklearn.cluster.KMeans
      • class sklearn.cluster.KMeans (n_clusters=8, init=’k-means++’, n_init=10, max_iter=300, tol=0.0001, precompute_distances=’auto’, verbose=0, random_state=None, copy_x=True, n_jobs=None, algorithm=’auto’)
      • 重要参数：
        • n_clusters（簇的个数）
          • n_clusters是KMeans中的k，表示着我们告诉模型我们要分几类。这是KMeans当中唯一一个必填的参数，默认为8 类，但通常我们的聚类结果会是一个小于8的结果。通常，在开始聚类之前，我们并不知道n_clusters究竟是多少， 因此我们要对它进行探索。
      • random_state(初始化质心)
        • 用于初始化质心的生成器。
  • KMeans的首次探索
    • 当我们拿到一个数据集，如果可能的话，我们希望能够通过绘图先观察一下这个数据集的数据分布，以此来为我们聚类时输入的n_clusters做一个参考。 首先，我们来自己创建一个数据集使用make_blobs。这样的数据集是我们自己创建，所以是有标签的。
    • 创建数据查看分类的散点图

from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 创建数据
# n_samples=500 原始数据有500行
# n_features=2  原始数据有2特征维度
# centers=4  原始数据有4个类别
x, y = make_blobs(n_samples=500, n_features=2, centers=4, random_state=10)
print(x.shape)
print(y.shape)
# 将原始已经有类别的样本数据绘制在散点图中，每一个类别使用不同颜色来表示
color = ['red', 'pink', 'orange', 'gray']
fig, ax1 = plt.subplots(1)  # 生成1个坐标系
for i in range(4):
    # 将X中y==i的类别的行第0列拿到,s为像素的大小
    ax1.scatter(x[y == i, 0], x[y == i, 1], c=color[i], s=8)
plt.show()
# 聚类分类-与原分类对比
# 用4个簇训练模型
cluster = KMeans(n_clusters=4)
cluster.fit(x)
# 重要属性Labels_，查看聚类后的类别，每个样本所对应的类
y_pred = cluster.labels_
# 重要属性cLuster_centers_，查看质心
cluster.cluster_centers_
# 重要属性inertia_，查看总距离平方和(整体平方和)
inertia = cluster.inertia_
color = ['red', 'pink', 'orange', 'gray']
fig, ax1 = plt.subplots(1)  # 生成1个坐标系
for i in range(4):
    # 将X中y==i的类别的行第0列拿到,s为像素的大小
    ax1.scatter(x[y_pred == i, 0], x[y_pred == i, 1], c=color[i], s=8)
plt.show()

• 聚类-predict
  • Kmeans对结果的预测
    • KMeans算法通常情况是不需要预测结果的，因为该算法本质上是在对未知分类数据的探索。但是在某些情况下我们也可以使用predict进行预测操作。
    • 我们什么时候需要predict呢？
      • 当数据量太大的时候！其实我们不必使用所有的数据来寻找质心，少量的数据就可以帮助我们确定质心了。当我们数据量非常大的时候，我们可以使用部分数据来帮助我们确认质心剩下的数据的聚类结果，使用predict来调用

inertia = cluster.inertia_
color = ['red', 'pink', 'orange', 'gray']
fig, ax1 = plt.subplots(1)  # 生成1个坐标系
for i in range(4):
    # 将X中y==i的类别的行第0列拿到,s为像素的大小
    ax1.scatter(x[y_pred == i, 0], x[y_pred == i, 1], c=color[i], s=8)
plt.show()
# 使用200组数据来寻找质心
c = KMeans(n_clusters=4, random_state=10)
c.fit(x[0:200])
print(c.predict(x[200:]))  # 和 labels_返回的结果一样，都是他的分到的类别

• 总结：数据量非常大的时候，效果会好。但从运行得出这样的结果，肯定与直接fit全部数据会不一致。有时候，当我们不要求那么精确，或者我们的数据量实在太大，那我们可以使用这种方法，使用接口predict。如果数据量还行，不是特别大，直接使用fit之后调用属性.labels_提出来聚类的结果。
• 逐步增加质心的数量，查看不同的Inertia
  • 随着簇增多，整体平方和变小

# 如果我们把猜测的簇数换成5
clustera = KMeans(n_clusters=5)
clustera.fit(x)
print(clustera.labels_)
print(clustera.inertia_)
# 如果我们把猜测的簇数换成6
clusterb = KMeans(n_clusters=6)
clusterb.fit(x)
print(clusterb.inertia_)

• 面试高危问题:如何衡量聚类算法的效果?
  • 聚类模型的结果不是某种标签输出，并且聚类的结果是不确定的，其优劣由业务需求或者算法需求来决定，并且没有永远的正确答案
    • 那我们如何衡量聚类的效果呢?
    • 聚类算法的模型评估指标
      • KMeans的目标是确保“簇内差异小，簇外差异大”，我们就可以通过衡量簇内差异来衡量聚类的效果。我们刚才说过，簇内平方和是用距离来衡量簇内差异的指标，因此，我们是否可以使用簇内平方和来作为聚类的衡量指标呢?簇内平方和越小模型越好嘛？
      • 可以，但是这个指标的缺点和极限太大。
      • 簇内平方和Inertia的缺点：
        • 1.首先，它不是有界的。我们只知道，Inertia是越小越好，是0最好，但我们不知道，一个较小的Inertia究竟有没有 达到模型的极限，能否继续提高。
        • 2.它的计算太容易受到特征数目的影响，数据维度很大的时候，Inertia的计算量会爆炸，不适合用来一次次评估模型。
        • 3.它会受到超参数K的影响，在我们之前的常识中其实我们已经发现，随着K越大，Inertia注定会越来越小，但 这并不代表模型的效果越来越好了
        • 4.使用Inertia作为评估指标，会让聚类算法在一些细长簇，环形簇，或者不规则形状的 流形时表现不佳：
          
        • 那我们可以使用什么指标呢?
          • 轮廓系数
    • 轮廓系数
      • 在99%的情况下，我们是对没有真实标签的数据进行探索，也就是对不知道真正答案的数据进行聚类。这样的聚类，是完全依赖于评价簇内的稠密程度(簇内差异小)和簇间的离散程度(簇外差异大)来评估聚类的效果。其中 轮廓系数是最常用的聚类算法的评价指标。它是对每个样本来定义的，它能够同时衡量:
      • 1)样本与其自身所在的簇中的其他样本的相似度a，等于样本与同一簇中所有其他点之间的平均距离
      • 2)样本与其他簇中的样本的相似度b，等于样本与下一个最近的簇中的所有点之间的平均距离 根据聚类的要求”簇内差异小，簇外差异大“，我们希望b永远大于a，并且大得越多越好。
      • $单个样本的轮廓系数计算为：s=\frac{b-a}{max(a,b)}$
    • 很容易理解轮廓系数范围是(-1,1):
      • 其中值越接近1表示样本与自己所在的簇中的样本很相似，并且与其他簇中的样本不相似，当样本点与簇外的样本更相似的时候，轮廓系数就为负。
      • 当轮廓系数为0时，则代表两个簇中的样本相似度一致，两个簇本应该是一个簇。可以总结为轮廓系数越接近于1越好，负数则表示聚类效果非常差。
    • 如果一个簇中的大多数样本具有比较高的轮廓系数，则簇会有较高的总轮廓系数，则整个数据集的平均轮廓系数越高，则聚类是合适的:
      • 如果许多样本点具有低轮廓系数甚至负值，则聚类是不合适的，聚类的超参数K可能设定得太大或者太小。
    • silhouette_score计算轮廓系数
      • 在sklearn中，我们使用模块metrics中的类silhouette_score来计算轮廓系数，它返回的是一个数据集中，所有样本的轮廓系数的均值。
    • silhouette_sample
      • 但我们还有同在metrics模块中的silhouette_sample，它的参数与轮廓系数一致，但返回的 是数据集中每个样本自己的轮廓系数
  • 计算轮廓系数

from sklearn.metrics import silhouette_score, silhouette_samples

# silhouette_score返回的是一个数据集中，所有样本的轮廓系数的均值
print(silhouette_score(x, labels=cluster.labels_))  # 每个样本的分类
# 返回的 是数据集中每个样本自己的轮廓系数
print(x.shape[0])
print(silhouette_samples(x, cluster.labels_))
print(silhouette_samples(x, cluster.labels_).sum() / x.shape[0])

支持向量机SVM概述

• 支持向量机(SVM，也称为支持向量网络)，是机器学习中获得关注最多的算法没有之一。
• 从实际应用来看
  • SVM在各种实际问题中都表现非常优秀。它在手写识别数字和人脸识别中应用广泛，在文本和超文本的分类中举足轻重。同时，SVM也被用来执行图像的分类，并用于图像分割系统。除此之外，生物学和许多其他科学都是SVM的青睐者，SVM现在已经广泛被用于蛋白质分类，现代化合物分类的业界平均水平可以达到90%以上的准确率。在生物科学的尖端研究中，人们还使用支持向量机来识别用于模型预测的各种特征，以找出各种基因表现结果的影响因素。
• 从学术的角度来看
  • SVM是最接近深度学习的机器学习算法。
• 支持向量机的原理
  • 支持向量机所作的事情其实非常容易理解。先来看看下面这一组数据的分布，这是一组两种标签的数据，两种标签分别由圆和方块代表。支持向量机的分类方法，是在这组分布中找出一个超平面作为决策边界，使模型在数据上的分类误差尽量接近于0，尤其是在未知数据集上的分类误差尽量小。
    
  • 超平面
    • 在几何中，超平面是一个空间的子空间，它是维度比所在空间小一维的空间。 如果数据空间本身是三维的， 则其超平面是二维平面，而如果数据空间本身是二维的，则其超平面是一维的直线。
    • 决策边界：在二分类问题中，如果一个超平面能够将数据划分为两个集合，其中每个集合中包含单独的一个类别，我们就说这个超平面是数据的“决策边界”。
    • 但是，对于一个数据集来说，让训练误差为0的决策边界可以有无数条。
      
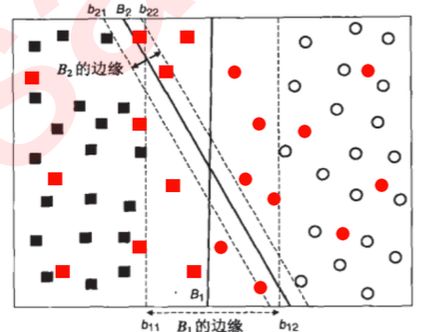
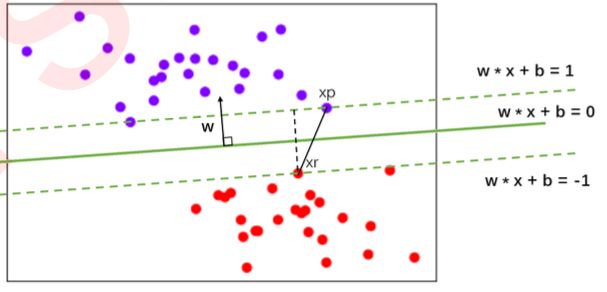
• 决策边界的边际
  • 在上图基础上，我们无法保证这条决策边界在未知数据集(测试集)上的表现也会优秀。对于现有的数据集来说，我们有B1和B2两条可能的决策边界。我们可以把决策边界B1向两边平移，直到碰到离这条决策边界最近的方块和圆圈后停下，形成两个新的超平面，分别是b11和b12，并且我们将原始的决策边界移动到b11和b12的中间，确保B1到b11和b12的距离相等。在b11和b12中间的距离，叫做B1这条决策边界的边际(margin)，通常记作d。
  • 为了简便，我们称b11和b12为“虚线超平面”，大家知道是这两个超平面是由原来的决策边界向两边移动，直到碰到距离原来的决策边界最近的样本后停下而形成的超平面就可以了.
  • 对B2也执行同样的操作，然后我们来对比一下两个决策边界。现在两条决策边界右边的数据都被判断为圆，左边 的数据都被判断为方块，两条决策边界在现在的数据集上的训练误差都是0，没有一个样本被分错。
  • 那么请思考，在测试集中，影响分类效果的因素是什么？
    
• 决策边界的边际对分类效果的影响
  • 我们引入和原本的数据集相同分布的测试样本(红色所示)，平面中的样本变多了，此时我们可以发现，对于B1而言，依然没有一个样本被分错，这条决策边界上的泛化误差也是0。但是对于B2而言，却有三个方块被误分类成了圆，而有两个圆被误分类成了方块，这条决策边界上的泛化误差就远远大于B1了。
  • 这个例子表现出，拥有更大边际的决策边界在分类中的泛化误差更小。如果边际很小，则任何轻微扰动都会对决策边界的分类产生很大的影响。边际很小的情况，是一种模型在训练集上表现很好，却在测试集上表现糟糕的情况，所以会“过拟合”。
  • 所以我们在找寻决策边界的时候，希望边际越大越好。
    
• 支持向量机分类原理
  • 支持向量机，就是通过找出边际最大的决策边界，来对数据进行分类的分类器。也因此，支持向量分类器又叫做最大边际分类器。这个过程在二维平面中看起来十分简单，但将上述过程使用数学表达出来，就不是一件简单的事情了。
• 如何找出边际最大的决策边界
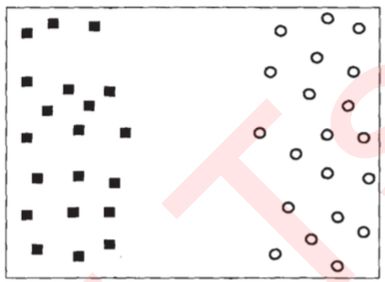
  • 假设现在数据集中有N个训练样本，每个训练样本i可以表示为(xi,yi)（i=1,2,3…N）,其中xi是的特征向量维度为二。二分类的标签yi的取值为（1，-1）这两类结果。接下来可视化我们的N个样本数据的特征数据：（紫色为一类，红色为另一类，）
    
  • 我们让所有紫色点的标签为1，红色点的标签为-1。我们要在这个数据集上寻找一个决策边界，在二维平面上，决 策边界(超平面)就是一条直线。二维平面上的任意一条线可以被表示为:$x_1=a{x}_2+b$
  • 我们将表达式变换一下：等号左边-等号右边=0
    
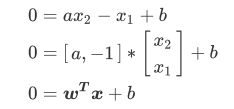
  • 其中[a, -1]就是我们的参数向量 ， X就是我们的特征向量， b是我们的截距。
  • 这个公式跟线性回归公式很像，但是线性回归公式等号的左边为我们预测出的结果，而现在的公式表示我们要找出决策边界。
• 在一组数据下，给定固定的w和b ，这个式子就可以是一条固定直线，在 w和 b不确定的状况下，这个表达式就可以代表平面上的任意一条直线。如果在w 和b 固定时，给定一个唯一的 x的取值，这个表达式就可以表示一个固定的点。那么固定下来的直线就可以作为SVM的决策边界。
• 在SVM中，我们就使用这个表达式来表示我们的决策边界。我们的目标是求解能够让边际最大化的决策边界，所以我们要求解参数向量 w和截距 b

  • 如果在决策边界上任意取两个点xa ，xb ，并带入决策边界的表达式，则有:

  • 将两式相减，可以得到:
    

    • 一个向量的转置乘以另一个向量，可以获得两个向量的点积(dot product)。两个向量的点积为0表示两个向量的方向是互相垂直的。这是线性代数中的基础结论！xa与xb是一条直线上的两个点，相减后的得到的向量方向是由xa指向xb，所以xa-xb的方向是平行于他们所在的直线-》我们的决策边界的。而w与xa-xb相互垂直，所以 参数向量w的方向必然是垂直于我们的决策边界。
    • 此时我们就有了决策边界（决策边界上任意一点对应的y值为0）。图中任意一个紫色的点xp可以表示为：
    • w*xp+b=p
      • 紫色点所表示的标签为y是1，所以我们规定p>0。

  • 同样，对于任意一个红色的点xr来讲，我们可以将它表示为：

    • w*xr+b=r
      • 红色点所表示的标签y是-1，所以我们规定r<0。

  • 此时，我们如果有新的测试数据xt，则的 标签就可以根 据以下式子来判定:
    

  • 我们之前说过，决策边界的两边要有两个超平面，这两个超平面在二维空间中就是两条平行线(就是我们的虚线超平面)，而他们之间的距离就是我们的边际d。而决策边界位于这两条线的中间，所以这两条平行线必然是对称的。我们另这两条平行线被表示为:
    

  • 支持向量：

    • 此时，我们可以让这两条线分别过两类数据中距离我们的虚线决策边界最近的点，这些点就被称 为“支持向量”，而决策边界永远在这两条线的中间。我们令紫色类的点为xp，红色类的点为xr（xp和xr作为支持向量）， 则我们可以得到:
      
    • 两式相减是为了求出两条虚线之间的距离

  • 如下图所示，（xp-xr）可表示为两点之间的连线(距离)，而我们的边际d是平行于w的，所以我们现在，相当于是得到了三角型中的斜边，并且知道一条直角边的方向。在线性代数中，我们有如下数学性质:

    • 向量a乘以向量b方向上的单位向量，可以得到向量a在向量b方向上的投影的长度。
    • xp-xr作为向量a，则w作为向量b，则可以求出边际的长度
    • 向量b除以自身的模长||b||可以得到b方向上的单位向量。
      

  • 所以，我们将上述式子两边除以||w||，可以得到：（这里多除一个||w||为了简化公式，有一定影响，但影响不大）

  • 还记得我们想求什么吗?最大边界所对应的决策边界，那问题就简单了，要最大化d，就求解w的最小值。我们可以把求解 的最小值转化为，求解以下函数的最小值:
    

    • 只所以要在模长上加上平方，是因为模长的本质是一个距离（距离公式中是带根号的），所以它是一个带根号的存在，我们对它取平方，是为了消除根号，不带平方也可以。
    • 我们的两条虚线表示的超平面，表示的是样本数据边缘所在的点。所以对于任意样本i，我们可以把决策函数写作:
      

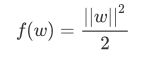
  • 如果wxi+b>=1，yi=1则yi(wxi+b)的值一定是>=1的，如果wxi+b<=-1，yi=-1则yi(wxi+b)的值也一定是>=1的。

• 至此，我们就得到了支持向量机的损失函数：
  
• 拉格朗日乘数
  • **有了我们的损失函数过后，我们就需要对损失函数进行求解。我们的目标是求解让损失函数最小化的w，但其实很容易看得出来，如果||w||为0，f(w)必然最小了。但是,||w||=0其实是一个无效的值，原因:首先，我们的决策边界是wx+b=0 ，如果w 为0，则这个向量里包含的所有元素都为0，那就有b = 0这个唯一值。然而，如果b和w都为0，决策边界就不再是一条直线了，条件中的yi(wxi+b)>=1就不可能实现，所以w不可以是一个0向量。可见，单纯让f(w)=||w||2/2 为0，是不能求解出合理的w的，我们希望能够找出一种方式，能够让我们的条件yi(wxi+b)>=1在计算中也被纳入考虑，一种业界认可的方法是使用拉格朗日乘数法。
  • 拉格朗日乘数涉及到的数学的难度不是推导损失函数的部分可比。并且，在sklearn当中，我们作为使用者完全无法干涉这个求解的过程。因此作为使用sklearn的人，这部分内容可以忽略不计。
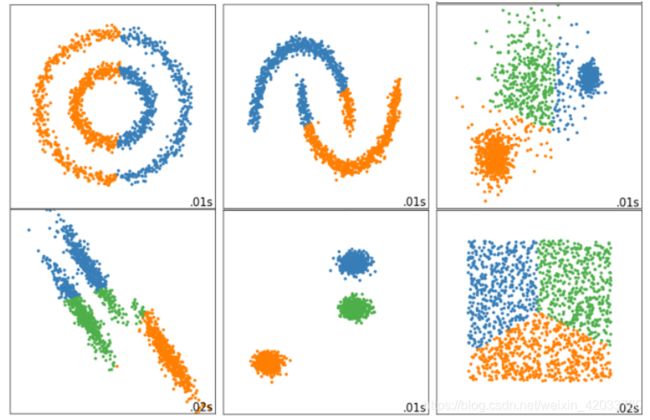
• 非线性SVM与核函数
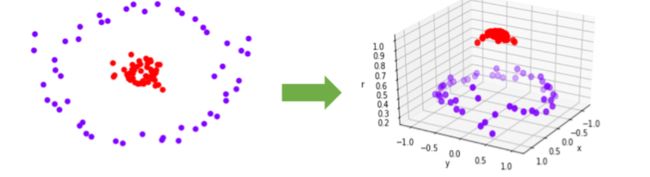
  • 当然，不是所有的数据都是线性可分的，不是所有的数据都能一眼看出，有一条直线，或一个平面，甚至一个超平面可以将数据完全分开。比如下面的环形数据。对于这样的数据，我们需要对它进行一个升维变化，让数据从原始的空间x投射到新空间q(x)中。升维之后，我们明显可以找出一个平面，能够将数据切分开来。
    • q(x)是一个映射函数，它代表了某种能够将数据升维的非线性的变换，我们对数据进行这样的变换，确保数据在自己的空间中一定能够线性可分。
      
  • 核函数
    • 上述这种手段是有问题的，我们很难去找出一个函数q(x)来满足我们的需求，并且我们并不知道数据究竟被映射到了一个多少维度的空间当中，有可能数据被映射到了无限空间中，让我们的计算和预测都变得无比艰难。所以无法统一定义一个固定的q(x)函数。为了避免这些问题，我们使用核函数来帮助我们。
    • 核函数K(xi,xtest)能够用原始数据空间中的向量计算来表示升维后的空间中的点积q(x)*q(xtest)，以帮助我们寻找合适的q(x)。选用不同的核函数，就可以解决不同数据分布下的寻找超平面问题。
    • 在sklearn的SVM中，这个功能由参数“kernel”(ˈkərnl)和一系列与核函数相关的参数来进行控制.因此我们更加重视不同的核函数选择对模型产生的影响是什么，而不是搞明白核函数的推导原理。
      
• 探索核函数在不同数据集上的表现
  
• 观察结果
  • 可以观察到，线性核函数和多项式核函数在非线性数据上表现会浮动，如果数据相对线性可分，则表现不错，如果是像环形数据那样彻底不可分的，则表现糟糕。在线性数据集上，线性核函数和多项式核函数即便有扰动项也可以表现不错，可见多项式核函数是虽然也可以处理非线性情况，但更偏向于线性的功能。
  • Sigmoid核函数就比较尴尬了，它在非线性数据上强于两个线性核函数，但效果明显不如rbf，它在线性数据上完全 比不上线性的核函数们，对扰动项的抵抗也比较弱，所以它功能比较弱小，很少被用到。
  • rbf，高斯径向基核函数基本在任何数据集上都表现不错，属于比较万能的核函数。我个人的经验是，无论如何先 试试看高斯径向基核函数，它适用于核转换到很高的空间的情况，在各种情况下往往效果都很不错，如果rbf效果 不好，那我们再试试看其他的核函数。另外，多项式核函数多被用于图像处理之中。
  • 模型参数：from sklearn.svm import SVC
  • kernel：选择核函数
  • C：正则化力度，处理过拟合。
  • class_weight：类别分布不均衡处理
• 问题：如何知道我们的数据集到底是线性可分的还是线性不可分的呢？因为我们需要为此选择不同的核函数。
• 处理：使用PCA降维，初步任意选取两种特征，将其映射在散点图中查看是否线性可分。

from sklearn.datasets import load_breast_cancer
from sklearn.decomposition import PCA
from sklearn.svm import SVC, SVR  # SVC做分类，SVR做回归预测
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

x = load_breast_cancer().data
y = load_breast_cancer().target
print(x.shape)
print(y.shape)
# 使用PCA对特征数据降维，查看是否线性可分
pca = PCA(n_components=2)  # n_components=2将数据降到2维
pca_x = pca.fit_transform(x)
print(pca_x.shape)
# 绘制散点图查看是否线性可分
plt.scatter(pca_x[:, 0], pca_x[:, 1], c=y)
plt.show()
# 由图可以看出数据大概是个偏线性可分
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=2021)
# 参数C正则化力度处理过拟合，kernel核函数，class_weight处理样本不均衡
s = SVC(C=1, kernel='linear').fit(x_train, y_train)
print(s.score(x_test, y_test))
s1 = SVC(C=1, kernel='poly').fit(x_train, y_train)
print(s1.score(x_test, y_test))
s2 = SVC(C=1, kernel='rbf').fit(x_train, y_train)
print(s2.score(x_test, y_test))

什么是EDA

• 在拿到数据后，首先要进行的是数据探索性分析（Exploratory Data Analysis），它可以有效的帮助我们熟悉数据集、了解数据集。初步分析变量间的相互关系以及变量与预测值之间的关系，并且对数据进行初步处理，如：数据的异常和缺失处理等，以便使数据集的结构和特征让接下来的预测问题更加可靠。
• 并且对数据的探索分析还可以：
  • 1.获得有关数据清理的宝贵灵感（缺失值处理，特征降维等）
  • 2.获得特征工程的启发
  • 3.获得对数据集的感性认识
  • 意义：数据决定了问题能够被解决的最大上限，而模型只决定如何逼近这个上限。
• EDA流程

  • 1、载入数据并简略观察数据

  • 2、总览数据概况

    • 在 describe 中有每一列的统计量、均值、标准差、最小值、中位数 25% 50% 75%以及最大值。可以帮助我们快速掌握数据的大概范围和数据的异常判断。
    • 通过 info 来了解每列的 type 和是否存在缺失数据。
    • 通过 isnull().sum() 查看每列缺失情况

  • 3、通过 describe 和 matplotlib 可视化查看数据的相关统计量（柱状图）

    • 重点查看方差为0或者极低的特征
    • 数据异常:
      
    • 正常值:

    

  • 4、缺失值处理

  • 5、查看目标数据的分布

    • 重点查看是否有
      • 分类：类别分布不均衡
        • 可以考虑使用过抽样处理
      • 回归：离群点数据
        • 可以考虑将离群点数据去除
    • 存在着一些特别大或者特别小的值，这些可能是离群点或记录错误点，对我们结果会有一些影响的。那我们是需要将离群点数据进行过滤的。
    • 离群点：离群点是指一个数据序列中，远离序列的一般水平的极端大值和极端小值，且这些值会对整个数据的分析产生异常的影响

  • 6、特征分布

    • 绘制数字特征的分布（直方图）
      • 可以观测特征为连续性和还是离散型特征
      • 可以观测特征数值的分布
      • 是否有离群点
    • 绘制类别特征的分布（柱状图）
      • 查看该特征中是否有稀疏类，在构建模型时，稀疏类往往会出现问题当然也不是绝对的。如果当前特征比较重要则可以将特征的稀疏类数据删除
        

  • 7、查看特征于特征之间的相关性（热力图）

    • 相关性强的特征就是冗余特征可以考虑去除。通常认为相关系数大于0.5的为强相关。

  • 8、查看特征和目标的相关性，正负相关性越强则特征对结果影响的权重越高，特征越重要

• 数据集背景介绍
  • 2009年的《纽约市基准法律》要求对建筑的能源和水的使用信息进行说明和评分。 涵盖的建筑包括具有单个建筑物的总建筑面积超过50,000平方英尺（平方英尺），和群建筑面积超过100,000平方英尺。指标是由环境保护署的工具ENERGY STAR Portfolio Manager计算的，并且数据由建筑物所有者自行报告。(回归问题)
  • 字段说明
    • 目标数据：
      ENERGY STAR Score：指定建筑物类型的1到100百分位排名，在投资组合管理器中根据自我报告计算报告年度的能源使用情况。

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

data = pd.read_csv('Energy.csv')
print(data.head(1))
# 查看数据形状
print(data.shape)
# 查看数据字段类型是否存在缺失值
print(data.info)
# 首先将"Not Available"替换为 np.nan
data = data.replace({'Not Available': np.nan})
print(data.info)
# 数据集有的字段显示为数值型数据，但是实际类型为str，再将部分数值型数据转换成float
for col in list(data.columns):
    if ('ft²' in col or 'kBtu' in col or 'Metric Tons CO2e' in col or 'kWh' in
            col or 'therms' in col or 'gal' in col or 'Score' in col):
        data[col] = data[col].astype(float)
print(data.describe())
# 通过 describe 和 matplotlib 可视化查看数据的相关统计量（柱状图）
data_desc = data.describe()  # 查看数据描述
cols = data_desc.columns  # 取得列缩影
index = data_desc.index[1:]  # 去除count行
plt.figure(figsize=(30, 30))  # 控制画布大小
for i in range(len(cols)):
    ax = plt.subplot(10, 6, i + 1)  # 绘制10x6的表格，当前数据特征维度为60
    ax.set_title(cols[i])  # 设置标题
    for j in range(len(index)):
        plt.bar(index[j], data_desc.loc[index[j], cols[i]])  # 对每个特征绘制describe柱状图
plt.show()


# Order的图形比较正常，因为最小值，中位数，最大值是错落分布，正常分布的，且均值和标准差分布也正常
# DOF Gross Floor Area图形可能有问题，显示最大值比其他的值都大很多(离均点,异常值)，如果最大值的数据数量较少，则考虑将其删除
# 发现：经度，维度特征的std极低，且数值分布特别均匀，说明这俩列特征对结果影响几乎为0，适当考虑过滤该特征


# 查看缺失值
def missing_values_table(df):
    # 计算每一列缺失值的个数
    mis_val = df.isnull().sum(axis=0)
    # 计算每列缺失值占该列总数据的百分比
    mis_val_percent = 100 * mis_val / data.shape[0]
    # 将每一列缺失值的数量和缺失值的百分比级联到一起,形成一个新的表格
    mis_val_table = pd.concat([mis_val, mis_val_percent], axis=1)
    # 重新给上步表格的列命名
    mis_val_table_ren_columns = mis_val_table.rename(columns={0: 'Missing Values', 1: '% of Total Values'})
    # 将百分比不为0的行数据根据百分比进行降序排序
    mis_val_table_ren_columns = mis_val_table_ren_columns[mis_val_table_ren_columns.iloc[:, 1] != 0].sort_values(
        '% of Total Values', ascending=False).round(1)
    # 打印概述
    print('Your selected dataframe has ' + str(df.shape[1]) + 'columns.\n'
                                                              'There are' + str(
        mis_val_table_ren_columns.shape[0]) + ' columns that have missing values.')
    # Return the dataframe with missing information
    return mis_val_table_ren_columns


missing_df = missing_values_table(data)
print(missing_df.head(3))
# 设置阈值将缺失比例超过百分之50的列删除
# 找出超过阈值的列
missing_df = missing_values_table(data)
missing_columns = list(missing_df.loc[missing_df['% of Total Values'] > 50].index)
print('We will remove %d columns.' % len(missing_columns))
data = data.drop(columns=list(missing_columns))
# print(data)
# 中位数填充剩下的空值 np.median获取中位数，如果原始数据存在空值就会返回空nan
for x in data.columns:
    # 去除object类型的列(object列不存在中位数)
    if str(data[x].dtypes) == 'object':
        continue
    if data[x].isnull().sum() > 0:
        # 取出每列非空元素求得中位数进行填充
        data[x] = data[x].fillna(value=np.median(data.loc[~data[x].isnull(), x]))
# 查看目标数据的分布情况
data['ENERGY STAR Score'].hist(bins=20)
plt.figure(figsize=(40, 20))
plt.scatter(data['ENERGY STAR Score'].index, data['ENERGY STAR Score'].values)
# 由图看到集中到60多出现一条线，说明数据集中在60多，没有找到离群数据
plt.show()
print(data['ENERGY STAR Score'].value_counts().sort_values().tail(1))

• 发现分布在65的数据量是最多的，没有发现离群数据
• 什么是离群点数据？
  • 存在着一些特别大或者特别小的值，这些可能是离群点或记录错误点，对我们结果会有一些影响的。那我们是需要将离群点数据进行过滤的。
  • 离群点：离群点是指一个数据序列中，远离序列的一般水平的极端大值和极端小值，且这些值会对整个数据的分析产生异常的影响。
  • 传统的过滤方式：
    • Q1 - 3 * IQ：Q1为序列中25%的中位数，IQ为Q3-Q1
    • Q3 + 3 * IQ：Q3为序列中75%的中位数，IQ为Q3-Q1
  • 离群点判定：
    • 极小的离群点数据：x < (q1 - 3 * iq)
    • 极大的离群点数据：x > (q3 + 3 * iq)
      
• 假设我们的目标数据为Site EUI (kBtu/ft²)
  • 寻找离群点

# data['Site EUI (kBtu/ft²)'].hist(bins=20)
# plt.figure(figsize=(15, 8))
# plt.scatter(data['Site EUI (kBtu/ft²)'].index, data['Site EUI (kBtu/ft²)'].values)
# plt.show()
# 离群点数据过滤
q1 = data['Site EUI (kBtu/ft²)'].describe()['25%']
q3 = data['Site EUI (kBtu/ft²)'].describe()['75%']
iq = q3 - q1
# data_copy就是离群的数据
data_copy = data[(data['Site EUI (kBtu/ft²)'] > (q1 - 3 * iq)) & (data['Site EUI (kBtu/ft²)'] < (q3 + 3 * iq))]
# 之后我们就可以对离群点做处理，替换replace还是删除
data_copy['Site EUI (kBtu/ft²)'].hist(bins=30)
plt.scatter(data_copy['Site EUI (kBtu/ft²)'].index, data_copy['Site EUI (kBtu/ft²)'].values)
plt.show()

• 特征数据的分布
  • 可以观测到特征的取值范围
  • 可以观测到特征不同数值的分布的密度
  • 可以观测到特征是连续性还是离散型
• 查看特征的不同取值数量

# 查看特征的不同取值数量
for x in data.columns:
    print('*' * 50)
    print(x, data[x].nunique())
    # 取值少的可能为类别性数据，取值多的为连续性数据
#  图形查看所有特征数据分布
import seaborn as sns

for col in data.columns:
    if 'int' in str(data[col].dtypes) or 'float' in str(data[col].dtypes):
        plt.hist(data[col], bins=50)
        sns.distplot(data.loc[~data[col].isnull(), col])
        plt.title(col)
        plt.show()
# 发现有很多特征都是长尾分布的，需要将其转换为正太或者近正太分布，长尾分布说明特征中少数的数值是离群点数据

• 长尾分布说明特征中少数的数值是离群点数据，需要将其转换为正太或者近正太分布了，log操作转换为近正太分布
• log操作转换为近正太分布

# log操作转换为近正太分布
# data['DOF Gross Floor Area']
sns.distplot(np.log(data.loc[~data['DOF Gross Floor Area'].isnull(), 'DOF Gross Floor Area']))
# plt.show()
# 直方图
for col in data.columns:
    if 'int' in str(data[col].dtypes) or 'float' in str(data[col].dtypes):
        plt.hist(data[col], bins=50)
        plt.title(col)
        plt.show()

• 类别型特征的特征值化
  • 结合着项目的目的和对非数值型字段特征的理解等手段，我们只选取出两个代表性特征Borough和Largest Property Use Type对其进行onehot编码实现特征值化

feature = data.loc[:, data.columns != 'ENERGY STAR Score']  # 提取特征数据
fea_name = feature.select_dtypes('number').columns  # 提取数值型特征名称
feature = feature[fea_name]  # 提取数值型特征
# 提取指定的两个类别型特征
categorical_subset = data[['Borough', 'Largest Property Use Type']]
categorical_subset = pd.get_dummies(categorical_subset)
feature = pd.concat([feature, categorical_subset], axis=1)

• 探索特征之间的相关性
  • corr查看特征与特征的相关性

print(feature.corr())  # corr查看特征与特征的相关性
plt.subplots(figsize=(30, 15))  # 指定窗口尺寸（单位英尺）
feature_corr = feature.corr().abs()  # 返回列与列之间的相关系数 abs求得是绝对值，相关系数与正负无关
# 数据为相关系数，显示数值，显示颜色条 这里需要导入模快 import seaborn as sns 也是一个绘图模块
sns.heatmap(feature_corr, annot=True)
plt.show()

• 去除相关性强的冗余特征，工具包封装如下

colsa = feature.columns  # 获取列的名称
corr_list = []
size = feature.shape[1]
# print(size)
high_corr_fea = []  # 存储相关系数大于0.5的特征名称
for i in range(0, size):
    for j in range(i + 1, size):
        if (abs(feature_corr.iloc[i, j]) >= 0.5):
            corr_list.append([feature_corr.iloc[i, j], i, j])  # features_corr.iloc[i,j]：按位置选取数据
sorted_corr_list = sorted(corr_list, key=lambda xx: -abs(xx[0]))
# print(sorted_corr_list)
for v, i, j in sorted_corr_list:
    high_corr_fea.append(colsa[i])
    # print("%s and %s = %.2f" % (cols[i], cols[j], v))  # cols: 列名
# 删除特征
feature.drop(labels=high_corr_fea, axis=1, inplace=True)
print(feature.shape)

• 查看特征和目标之间的相关性
  • 如果特征和标签之间是存在线性关系的才可以采用如下方式

target = data['ENERGY STAR Score']
target = pd.DataFrame(data=target, columns=['ENERGY STAR Score'])
# 级联target&feature
new_data = pd.concat((feature, target), axis=1)
# 计算相关性,之后我们就可以选择特征与目标相关性较大的数据进行特征的选取
fea_target_corr = abs(new_data.corr()['ENERGY STAR Score'][:-1])
print(fea_target_corr)

• 保存数据

# 改名字
new_data = new_data.rename(columns={'ENERGY STAR Score': 'score'})
# print(new_data)
new_data.to_csv('eda_data.csv')

• 建模 (该案例是回归问题)
  • 数据集导入及切分

from sklearn.model_selection import GridSearchCV, train_test_split

data = pd.read_csv('eda_data.csv').drop(labels='Unnamed:0', axis=1)
fea_name = [x for x in data.columns if x not in ['score']]
feature = data[fea_name]
target = data['score']
x_train, x_test, y_train, y_test = train_test_split(feature, target, test_size=0.2, random_state=2021)

• 选择的机器学习算法（回归问题）
  • 1.Linear Regression
    2.Support Vector Machine Regression
    3.Random Forest Regression
    4.lightGBM (忽略)
    5.xgboost
    • 我们只选择其默认的参数，这里先不进行调参工作，后续再来调参。
  • 由于模型的调用和评价方式是一样的，则封装如下工具函数

# Function to calculate mean absolute error
def mae(y_true, y_pred):
    return np.mean(abs(y_true-y_pred))
# Takes in a model, trains the model, and evaluates the model on the test set
def fit_and_evaluate(model):
    # Train the model
    model.fit(x_train, y_train)
    # Make predictions and evalute
    model_pred = model.predict(x_test)
    model_mae = mae(y_test, model_pred)
    # Return the performance metric
    return model_mae

• 尝试各种模型

# 线性回归
lr = LinearRegression()
lr_mae = fit_and_evaluate(lr)
print('Linear Regression Performance on the test set: MAE = %0.4f' % lr_mae)
# svm支向量机
svm = SVR(C=1000, gamma=0.1)
svm_mae = fit_and_evaluate(svm)
print('Support Vector Machine Regression Performance on the test set: MAE = %0.4f' % svm_mae)
# 随机森林
random_forest = RandomForestRegressor(random_state=60)
random_forest_mae = fit_and_evaluate(random_forest)
print('Random Forest Regression Performance on the test set: MAE = %0.4f' % random_forest_mae)
plt.style.use('fivethirtyeight')
model_comparison = pd.DataFrame({'model': ['Linear Regression', 'Support Vector Machine',
                                           'Random Forest'
                                           ],
                                 'mae': [lr_mae, svm_mae, random_forest_mae]})
model_comparison.sort_values('mae', ascending=False).plot(x='model', y='mae', kind='barh',
                                                          color='red', edgecolor='black')

plt.ylabel('')
plt.yticks(size=14)
plt.xlabel('Mean Absolute Error')
plt.xticks(size=14)
plt.title('Model Comparison on Test MAE', size=20)
plt.show()

• 看起来集成算法更占优势一些，这里存在一些不公平，因为参数只用了默认，但是对于SVM来说参数可能影响会更大一些。
• 模型调参 (这里用网格搜索找寻最佳参数)
  • 以随机森林参数调优为例

from sklearn.model_selection import GridSearchCV

parameters = {'n_estimators': [150, 200, 250], 'min_samples_split': [2, 3, 5, 10, 15]
    , "max_depth": [2, 3, 5, 10, 15]
    , 'min_samples_leaf': [1, 2, 4, 6, 8]
    , 'min_samples_split': [2, 4, 6, 10]
              }
model = RandomForestRegressor()
GS = GridSearchCV(estimator=model, param_grid=parameters, cv=5, scoring='neg_mean_absolute_error')
GS.fit(x_train, y_train)
print(GS.best_params_)