【数字信号处理】基于matlab LMD算法和ELMD算法管道泄漏信号处理【含Matlab源码 1985期】
一、局部分解理论研究
局部均值分解算法(Local Mean Decomposition, LMD) 作为处理非平稳随机信号的一种手段,得到了广泛应用,并成熟地应用于机械故障诊断、信号特征提取与分析等方面。LMD算法最大的特点就在于其对信号的自适应分解能力, 这种自适应能力主要体现在该方法能够通过数据自身特点,通过特定手段,将原始信号分为不同模态函数, 针对不同模态函数进一步处理。与此同时, 局部均值分解算法(LMD) 相较于模态分解的创始算法经验模态分解算法(Empirical Mode Decomposition, EMD) 而言,其具备端点效应小、迭代次数少等优势。本章将详述LMD算法基本原理及分解流程,并针对LMD存在的基本问题, 进行改进研究。
1 局部均值分解算法理论研究
2005年, JonathanS.Smith提出的一种新的非线性和非平稳信号分析方法一局部均值分解算法(LMD) , 并应用于脑电信号的分析中, 取得不错的效果。此外, 局部均值分解在机械故障诊断中也得到良好的应用。局部均值分解可以依据信号本身的特征进行自适应分解的,产生具有真实物理意义的PF分量,并由此得到能够清晰准确反映出信号能量在空间各尺度上分布规律的时频分布,有利于更加细致的对信号特征进行分析。
1.1局部均值算法(LMD) 分解流程
利用LMD分解, 可以将原始信号分解并产生若干有效PF分量, 将所有PF分量相加即可重构出原始信号。其中每个PF分量都是一个纯调频信号和包络信号的乘积,且每个PF分量的瞬时频率具有实际物理意义。LMD分解的具体流程如下:(1)原始信号x(t),找出x(t)上的所有局部极值点n,由相邻的两个极值点n,n.计算出的一个均值m,即
![]()
随后将得到的所有平均值m,用折线连接,连接过程采用滑动平均方法进行平滑处理,进而得到局部均值函数m,(t)。同时,利用相邻极值点计算包络估计值a,,即
![]()




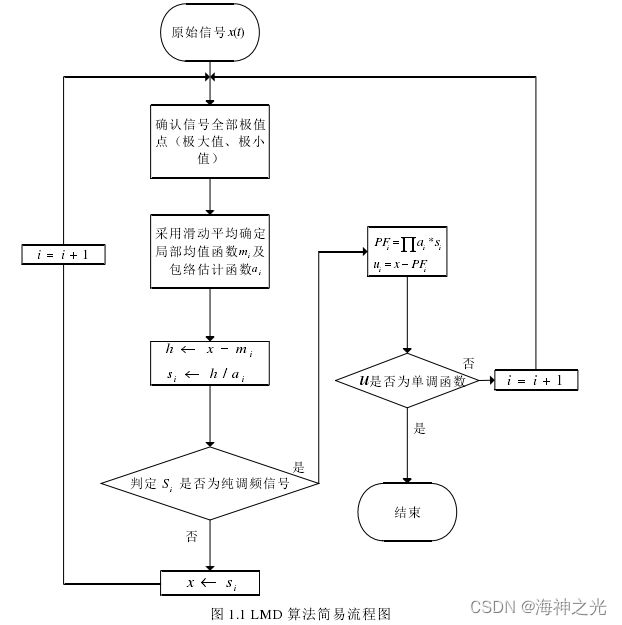
通过公式(2-12)可以发现,信号重构过程中,不会出现信息的丢失,保证了信号的完整性。具体流程图如下图1.1所示
(1)总体局部均值分解算法研究
模态混叠现象的发生一方面来自于算法本身,另一方面则会受到原始信号频率特征的影响。当待处理信号确定之后,信号特征频率变不会发生改变,因此,为抑制模态混叠现象的出现,从算法本身出发,引入噪声辅助信号处理方法,即在信号中加入白噪声来平滑脉冲干扰。因为在LMD分解过程中, 需要对极值点进行处理, 得到局部均值函数及包络估计函数,极值点的分布就会影响到包络的拟合情况。如果信号的极值点分布不均匀, 则极易产生模态混叠。因此, 在LMD中, 借助高斯白噪声辅助法, 对模态混叠进行抑制, 得到总体局部均值分解(Ensemble Local Mean Decomposition ELMD) 算法。ELMD分解, 是指在LMD分解前, 将不同有限幅值的白噪声信号加入待分解信号,利用白噪声均值为零,频谱能量分布均匀的特性,使得白噪声可以均匀的分布在整个时频空间中,并且不同时间尺度的信号会自动分布到与背景噪声相关的适当尺度上去。对于单次试验,由于噪声的添加,使得每次结果都会受到噪声的影响产生偏差,这是由于在分解过程中,信号包括原始信号及附加的白噪声。但随着试验的次数增加,由于零均值的特性,噪声将会相互抵消,进而得到消除,唯一持久稳固的部分便是信号本身, 因此可以认定集成均值的结果就是最终分解结果, 即EL MD算法。
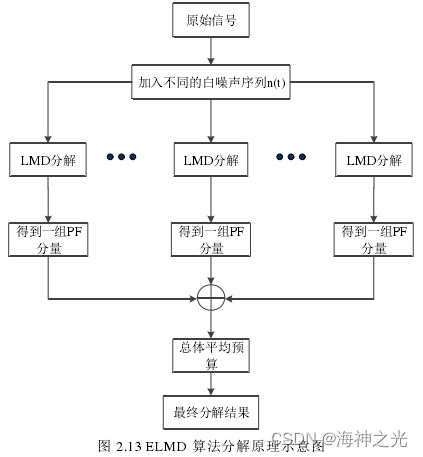
总体局部均值EL MD分解算法流程图如图2.13所示, 即对原始信号分别加入n组不同高斯白噪声, 分别进行LMD分解, 随后将得到的n组PF分量进行平均处理,得到最终的LMD分解结果。
二、部分源代码
clear;clc;close all;
x1=xlsread('5.xlsx');
VarName2=x1(:,2);
x=VarName2';
Nstd =0.1;
NR =100;
%[modes its]=eemd(ecg,0.1,100,1000);
modes = mlmd(x,Nstd,NR);
[a, b]=size(modes);
N=length(x);
fs=1000;
Ts=1/fs;
t=0:Ts:N*Ts;
t=t(1:N);
% 绘制仿真信号和其频谱图
figure(1)
subplot(211)
plot(t,x)
subplot(212)
y2=x;
L=length(y2);
NFFT = 2^nextpow2(L);
Y = fft(y2,NFFT)/L;
f = fs/2*linspace(0,1,NFFT/2);
plot(f,2*abs(Y(1:NFFT/2)))
PF=modes;
line=size(PF,1);
NN = length(PF(1,:));
n = linspace(0,1,NN);
for k1=0:4:line-1
figure('Color',[1 1 1]);
for k2=1:min(4,line-k1)
subplot(4,2,2*k2-1);
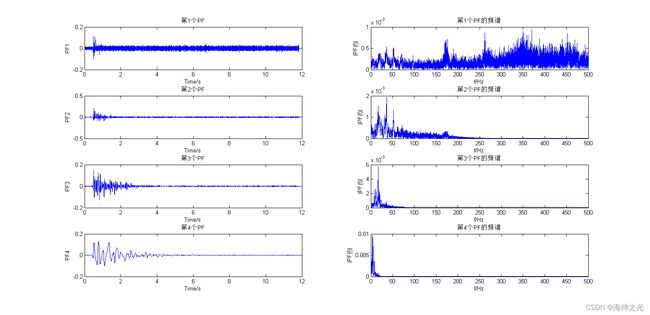
plot(t,PF(k1+k2,:));
title(sprintf('第%d个PF', k1+k2))
xlabel('Time/s')
ylabel(sprintf('PF%d',k1+k2));
subplot(4,2,2*k2)
[yf, f] = FFTAnalysis(PF(k1+k2,:), Ts);
plot(f, yf)
title(sprintf('第%d个PF的频谱', k1+k2))
xlabel('f/Hz')
ylabel('|PF(f)|');
end
end;
% 频谱分析
function [Y, f] = FFTAnalysis(y, Ts)
Fs = 1/Ts;
L = length(y);
NFFT = 2^nextpow2(L);
% y = y - mean(y);
Y = fft(y, NFFT)/L;
Y = 2*abs(Y(1:NFFT/2+1));
f = Fs/2*linspace(0, 1, NFFT/2+1);
end
function [pf,a,si,u] = lmd(x)
x=x';
c = x';
N = length(x);
A = ones(1,N);
PF = [];
AA=[];
SI=[];
U=[];
aii = 2*A;
while(1)
si = c;
a = 1;
while(1)
h = si;
maxVec = [];
minVec = [];
% look for max and min point
for i = 2: N - 1
if h (i - 1) < h (i) && h (i) > h (i + 1)
maxVec = [maxVec i];
end
if h (i - 1) > h (i) && h (i) < h (i + 1)
minVec = [minVec i];
end
end
% check if it is residual
if (length (maxVec) + length (minVec)) < 2
break;
end
% handle end point
lenmax=length(maxVec);
lenmin=length(minVec);
%left end point
if h(1)>0
if(maxVec(1)<minVec(1))
yleft_max=h(maxVec(1));
yleft_min=-h(1);
else
yleft_max=h(1);
yleft_min=h(minVec(1));
end
else
if (maxVec(1)<minVec(1))
yleft_max=h(maxVec(1));
yleft_min=h(1);
else
yleft_max=-h(1);
yleft_min=h(minVec(1));
end
end
%right end point
if h(N)>0
if(maxVec(lenmax)<minVec(lenmin))
yright_max=h(N);
yright_min=h(minVec(lenmin));
else
yright_max=h(maxVec(lenmax));
yright_min=-h(N);
end
else
if(maxVec(lenmax)<minVec(lenmin))
yright_max=-h(N);
yright_min=h(minVec(lenmin));
else
yright_max=h(maxVec(lenmax));
yright_min=h(N);
end
end
%get envelop of maxVec and minVec using
%spline interpolate
maxEnv=spline([1 maxVec N],[yleft_max h(maxVec) yright_max],1:N);
minEnv=spline([1 minVec N],[yleft_min h(minVec) yright_min],1:N);
mm = (maxEnv + minEnv)/2;
aa = abs(maxEnv - minEnv)/2;
mmm = mm;
aaa = aa;
preh = h;
h = h-mmm;
si = h./aaa;
a = a.*aaa;
aii = aaa;
B = length(aii);
C = ones(1,B);
bb = norm(aii-C);
if(bb < 1000)
break;
end
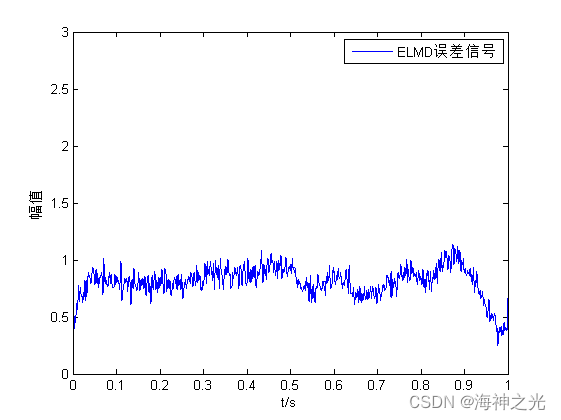
三、运行结果
四、matlab版本及参考文献
1 matlab版本
2014a或2019b
2 参考文献
[1]李博健.改进LMD算法在管道泄漏中的应用研究[D].东北石油大学
3 备注
简介此部分摘自互联网,仅供参考,若侵权,联系删除