Pytorch学习笔记09——多分类问题
Pytorch学习笔记09——多分类问题
在上一篇文章的糖尿病数据集当中,输出只有0和1俩种可能值。
P(y=0) = 1-P(y=1)
如何实现多分类问题?
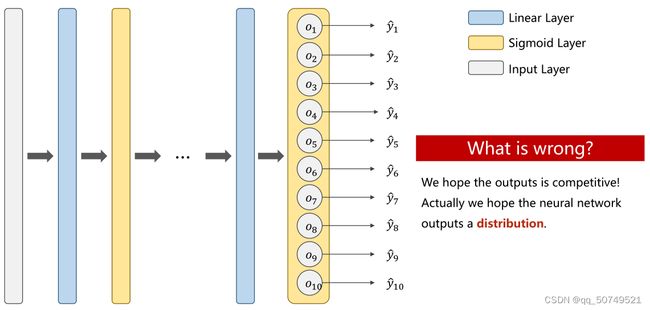
经过最后一步softmax后得到10个预测值,如果我们仍然用二分类的思维去想这个问题:
y1^hat属于第一类的概率是0.8, 不属于第一类的概率是0.2.
y2^hat属于第二类的概率是0.9, 不属于第二类的概率是0.1.
y3^hat属于第一类的概率是0.9, 不属于第一类的概率是0.1.
。。。。
y1^hat属于第一类的概率是0.3, 不属于第一类的概率是0.7.
这样就会产生矛盾了,我们希望输出是带有竞争性的,让他们的合为1,之间互相排斥。一个大了其他就小了。p(y = 0)、p(y = 1)…p(y = 9)整个我们希望他是符合一个概率分布的。
比如p(y=0)=0.8, p(y = 1、2…、8)=0.01,p(y = 10) = 0.12, 如下图所示,这是我们想要的表现。

Softmax就帮助我们做了这样一件事:
对最后一层输出的{y1, y2 …}作np.exp(), 计算总和Sum,再用np.exp(yi)/Sum就可以了。
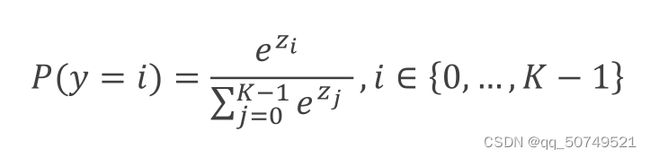
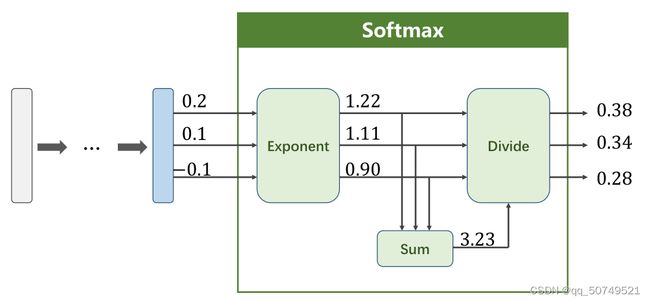
在上面的例子中,{0.2, 0.1, -0.1}经过softmax转成了{0.38, 0.34, 0.28}:
import numpy as np
import torch
x = torch.tensor([0.2, 0.1, -0.1])
y_softmax = np.exp(x)/np.exp(x).sum()
y_softmax
tensor([0.3780, 0.3420, 0.2800])
那么如何计算损失呢?
我们假设标签是1,就需要对1进行one-hot编码,与y_softmax长度对齐。

NLLLoss做的是红色方框里的事儿。我们需要自己写softmax。
import numpy as np
import torch
y = torch.tensor([1, 0, 0])
x = torch.tensor([0.2, 0.1, -0.1])
y_softmax = np.exp(x)/np.exp(x).sum()
loss = (-y * np.log(y_softmax)).sum()
loss.item()
0.9729189872741699
而crossentropy做的是下面红色方框的事儿。最后一层不需要再做softmax激活了,同样也不需要自己对标签one-hot编码。

import torch
y = torch.LongTensor([0])#注意使用长整型,0就表示one-hot后只有第0个是1
z = torch.Tensor([[0.2, 0.1, -0.1]])
criterion = torch.nn.CrossEntropyLoss()
loss = criterion(z, y)
loss.item()
0.9729189276695251
我们来看这样一段代码
criterion = torch.nn.CrossEntropyLoss()
Y = torch.LongTensor([2, 0, 1])#分别代表属于第2类、第0类、第1类
Y_pred1 = torch.Tensor([[0.1, 0.2, 0.9], #2
[1.1, 0.1, 0.2], #0
[0.2, 2.1, 0.1]]) #1
Y_pred2 = torch.Tensor([[0.8, 0.2, 0.3], #0
[0.2, 0.3, 0.5], #2
[0.2, 0.2, 0.5]])#2
loss1 = criterion(Y_pred1, Y)
loss2 = criterion(Y_pred2, Y)
print(loss1.item())
print(loss2.item())
Y_pred1很明显看起来更符合标签,结果也是如此。虽然[0.1, 0.2, 0.9]这里面并不是一个合为1的概率分布,但0.9也能看出来最大,是属于第二类的。
用全连接神经网络实现MNIST数据集分类
在mnist数据集当中,我们输入的是图像,这个图像上是0-9十个数字,我们需要进行十分类任务。那么如何将图像送到模型中训练呢?一种方式是我们可以把图像映射成一个矩阵,再送到模型中训练。
如下所示,这是一个28 * 28 = 784像素的图片,越深的地方越接近0,越亮的地方越接近1.


transform:pytorch读图像的时候,用的是python的PIL Image,
神经网络希望我们输入的数值比较小,这对训练是最有帮助的。 读入的时候值是0-255量化的,代表了256种亮度。我们要把他转成图像张量,并希望转成一个0-1之间的分布。
我们把这个黑白的叫做单通道的图像。我们看到的彩色图像有三个通道RGB.
正常处理的时候,我们读进来的图像是W * H* C样的,需要转成C * W * H,通道放第一位。这是为了在pytorch进行更高校的图像处理、卷积运算。
0-255压缩到0-1的浮点数。把28 * 28转换成1 * 28 * 28的图像张量.1 * 28 * 28, 1是通道,28分别是是宽和高。
在概率统计当中,我们学过把普通正态分布如何转换到标准正态分布N(0, 1):
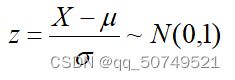
对于mnist数据集,均值mean为0.1307, 方差std为0.3081。
第一步,加载数据集:
batch_size = 64
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307, ), (0.3081, ))
])
train_dataset = datasets.MNIST(root='../dataset/mnist/',
train=True,
download=True,
transform=transform)
train_loader = DataLoader(train_dataset,
shuffle=True,
batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist',
train=False,
download=True,
transform=transform)
test_loader = DataLoader(test_dataset,
shuffle=False,
batch_size=batch_size)
把要下载的路径写到root里就可以自动下载了(无法下载记得挂)

我们来看一下train_loader和test_loader的信息
train_dataset
Dataset MNIST
Number of datapoints: 60000
Root location: …/dataset/mnist/
Split: Train
StandardTransform
Transform: Compose(
ToTensor()
Normalize(mean=(0.1307,), std=(0.3081,))
)
可以看到,这个训练集有60000个样本,我们构成的批量数据集是以batch_size=64为单位划分的,同时进行了Shuffle打乱操作。也就是说我们分成了60000/64=937块。训练时按照小批量进行训练。
test_dataset
Dataset MNIST
Number of datapoints: 10000
Root location: …/dataset/mnist/
Split: Test
StandardTransform
Transform: Compose(
ToTensor()
Normalize(mean=(0.1307,), std=(0.3081,))
)
Test测试集一共有10000个测试样本,同样也64个地测试。测试集不需要shuffle打乱,这方便我们以后查看哪里测试有问题。
四个.gz文件已经解压好了。
第二步:设计模型

class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.linear1 = torch.nn.Linear(784, 512)
self.linear2 = torch.nn.Linear(512, 256)
self.linear3 = torch.nn.Linear(256, 128)
self.linear4 = torch.nn.Linear(128, 64)
self.linear5 = torch.nn.Linear(64, 10)
self.relu = torch.nn.ReLU()
def forward(self, x):
x = x.view(-1, 784)
x = self.relu(self.linear1(x))
x = self.relu(self.linear2(x))
x = self.relu(self.linear3(x))
x = self.relu(self.linear4(x))
x = self.linear5(x)
return x
model = Net()
第三步:确定损失和优化器
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr = 0.01)
第四步:硬train一发
epoch_list = []
loss_list = []
loss_sum = 0
for epoch in range(10):
for index, data in enumerate(train_loader, 0):
inputs, labels = data
optimizer.zero_grad()
y_pred = model(inputs)
loss = criterion(y_pred, labels)
loss.backward()
optimizer.step()
loss_sum += loss.item()
batch = index
print('epoch = ', epoch, 'loss = ', loss_sum/batch)
epoch_list.append(epoch)
loss_list.append(loss_sum/batch)
loss_sum = 0
epoch = 0 loss = 1.8594086992702463
epoch = 1 loss = 0.463400487898349
epoch = 2 loss = 0.29753065994059075
epoch = 3 loss = 0.2263508649521061
epoch = 4 loss = 0.1784982799841618
epoch = 5 loss = 0.145680181410267
epoch = 6 loss = 0.1220758174344293
epoch = 7 loss = 0.10426992276661583
epoch = 8 loss = 0.09011199540051601
epoch = 9 loss = 0.07850728131541952

第五步:测试
total = 0
correct = 0
with torch.no_grad():
for data in test_loader:
images, labels = data
outputs = model(images)
_,predicted = torch.max(outputs.data, dim = 1)
total +=labels.size(0)
correct += (predicted == labels).sum().item()
print( 'Accuracy on test set: %d %%' % (100 * correct / total))
Accuracy on test set: 97 %
测试的时候,只需要前向传播计算输出即可,不涉及梯度。所以这里用了with torch.no_grad:
得到的输出outputs是一个(N, 10)的矩阵,对于这N个样本,我们只要找到每一行10个数里最大的数字就可以了,就能对应到属于哪一类。
_,predicted = torch.max(outputs.data, dim = 1)就是对output一行一行找最大值得操作。输出最大值及最大值索引。
Python 各种下划线都是啥意思_、xx、xx、__xx、xx、classname
End~~~