深度/机器学习基础知识要点：CTC算法
-
Connectionist Temporal Classification (CTC)
CTC适合语音识别和手写字符识别任务
-
定义
输入表示：符号序列 X = [ x 1 , x 2 , . . . , x T ] X=[x_{1},x_{2},...,x_{T}] X=[x1,x2,...,xT]
输出表示：符号序列 Y = [ y 1 , y 2 , . . . , y U ] Y=[y_{1},y_{2},...,y_{U}] Y=[y1,y2,...,yU]目标：找到输入X与输出Y之间精确的映射关系。
-
难点：
1、X和Y都是变长的
2、X和Y的长度比也是变化的
3、X和Y相应的元素之间没有严格的对齐(即 x t 与 y u x_{t}与y_{u} xt与yu不一定对齐)
-
-
损失函数的定义
对于给定的输入 X X X，我们训练模型希望最大化 Y Y Y的后验概率 P ( Y ∣ X ) , P ( Y ∣ X ) P(Y|X),P(Y|X) P(Y∣X),P(Y∣X)应该是可导的，这样我们就能利用梯度下降训练模型了。 -
预测
当我们已经训练好一个模型后，输入 X X X，我们希望输出 Y Y Y的条件概率最大，即Y ∗ = arg max Y p ( Y ∣ X ) Y*=\mathop{\arg\max}_{Y}p(Y|X) Y∗=argmaxYp(Y∣X)
希望尽量快速的得到 Y ∗ Y* Y∗ 值，利用CTC我们能在低投入情况下迅速找到一个近似的输出。
-
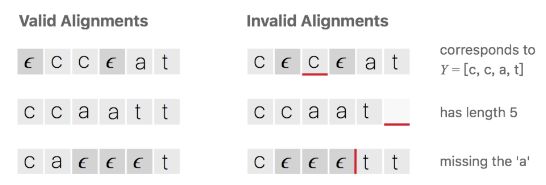
CTC的对齐
假设对于一段音频，我们希望的输出是 Y = [ c , a , t ] Y=[c,a,t] Y=[c,a,t] 这个序列，一种将输入输出进行对齐的方式如下图所示，先将每个输入对应一个输出字符，然后将重复的字符删除。
上述对齐方式有两个问题：
1、通常这种对齐方式是不合理的。比如在语音识别任务中，有些音频片可能是无声的，这时候应该是没有字符输出的。
2、对于一些本应含有重复字符的输出，这种对齐方式没法得到准确的输出。例如输出对齐的结果为 [ h , h , e , l , l , l , o ] [h,h,e,l,l,l,o] [h,h,e,l,l,l,o]，通过去重操作后得到的不是“hello”而是“helo”。为了解决上述问题，CTC算法引入的一个新的占位符用于输出对齐的结果。这个占位符
称为空白占位符，通常使用符号 ϵ \epsilon ϵ。则上图变成：
-
下图说明有效对齐和无效对齐
-
CTC算法的对齐方式有下列属性：
1、输入与输出的对齐方式是单调的，即如果输入下一输入片段时输出会保持不变或者也会移动到下一个时间片段
2、输入与输出是多对一的关系
3、输出的长度小于等于输入
-
-
损失函数
对于一对输入输出(X,Y)来说，CTC的目标是将下式概率最大化：
CTC算法采用动态规划的思想来求解输出的条件概率，下图说明的是通过动态规划来进行路径的合并：
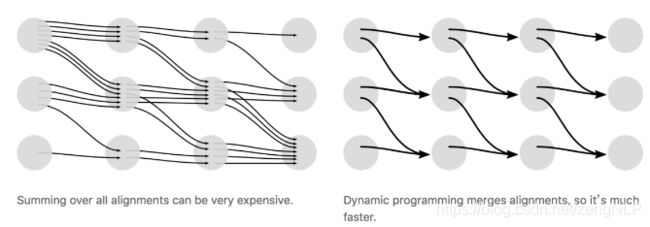假设我们现在有输入音频X对应的标定输出Y为单词“ZOO”，为了方便解释下面动态规划的思想，现在每个字符之间还有字符串的首位插入空白占位符 ϵ \epsilon ϵ，得到下面结果
Z = { ϵ , Z , ϵ , O , ϵ , O , ϵ } Z=\{\epsilon,Z,\epsilon,O,\epsilon,O,\epsilon\} Z={ϵ,Z,ϵ,O,ϵ,O,ϵ}定义：横轴是X的时间片单位为t，纵轴为Z序列单位为s。
根据CTC的对齐方式的三个特征，输入有9个时间片，标签内容是“ZOO”，P(Y|X)的所有可能的合法路径如下图：
α s , t \alpha_{s,t} αs,t表示上图中坐标为(s,t)节点的概率，该点的概率计算分为下面两种情况：
情况 1：
1）如果 α s , t = ϵ \alpha_{s,t}=\epsilon αs,t=ϵ，则 α s , t \alpha_{s,t} αs,t只能由前一个字符 α s − 1 , t − 1 \alpha_{s-1,t-1} αs−1,t−1或者本身 α s , t − 1 \alpha_{s,t-1} αs,t−1得到
2）如果 α s , t \alpha_{s,t} αs,t不等于 ϵ \epsilon ϵ，但是 α s , t \alpha_{s,t} αs,t为连续字符的第二个，即 α s = α s − 2 ( α s − 1 = ϵ ) \alpha_{s}=\alpha_{s-2}(\alpha_{s-1}=\epsilon) αs=αs−2(αs−1=ϵ)，则 α s , t \alpha_{s,t} αs,t只能由一个空白符 α s − 1 , t − 1 \alpha_{s-1,t-1} αs−1,t−1或者其本身 α s , t − 1 \alpha_{s,t-1} αs,t−1得到，而不能由前一个字符得到。上述两种情况中， α s , t \alpha_{s,t} αs,t可以由下式算出，其中 p t ( z s ∣ X ) p_{t}(z_{s}|X) pt(zs∣X)表示在时刻t输出字符 z s z_{s} zs的概率。
α s , t = ( α ( s , t − 1 ) + α ( s − 1 , t − 1 ) ) ⋅ p t ( z s ∣ X ) \alpha_{s,t}=(\alpha(s,t-1)+\alpha(s-1,t-1))\cdot p_{t}(z_{s}|X) αs,t=(α(s,t−1)+α(s−1,t−1))⋅pt(zs∣X)情况 2：
如果 α s , t \alpha_{s,t} αs,t不等于 ϵ \epsilon ϵ，则 α s , t \alpha_{s,t} αs,t可以由 α s , t − 1 \alpha_{s,t-1} αs,t−1， α s − 1 , t − 1 \alpha_{s-1,t-1} αs−1,t−1以及 α s − 2 , t − 1 \alpha_{s-2,t-1} αs−2,t−1得来，可以表示为
α s , t = ( α ( s , t − 1 ) + α ( s − 1 , t − 1 ) + α ( s − 2 , t − 1 ) ) ⋅ p t ( z s ∣ X ) \alpha_{s,t}=(\alpha(s,t-1)+\alpha(s-1,t-1)+\alpha(s-2,t-1))\cdot p_{t}(z_{s}|X) αs,t=(α(s,t−1)+α(s−1,t−1)+α(s−2,t−1))⋅pt(zs∣X)从上图可以看到合法路径由两个起始点，输出两个终止点，最后输出的条件概率为两个终止点输出概率的和。
-
CTC的特征
1、条件独立：CTC的一个非常不合理的假设是其假设每个时间片都是相互独立的，这是一个非常不好的假设。在OCR或者语音识别中，各个时间片之间是含有一些语义信息的，所以如果能够在CTC中加入语言模型的话效果应该会有提升。
2、单调对齐：CTC的另外一个约束是输入X与输出Y之间的单调对齐，在OCR和语音识别中，这种约束是成立的。但是在一些场景中例如机器翻译，这个约束便无效了。
3、多对一映射：CTC的又一个约束是输入序列X的长度大于标签数据 Y的长度，但是对于X的长度大于Y的长度的场景，CTC便失效了。 -
其他详情参考：
CTC算法详解