VFH*避障/局部路径规划算法

做个正直的人

VFH*是VFH、VFH+两个算法的持续改进，对这两个算法不熟悉的同学，不建议直接看这一篇文章。可以去看我写的两篇介绍VFH、VFH+算法的文章。

先说一下这三个算法的关系。VFH（Vector Field Histogram）的前身是VFF（Virtual Force Field），VFH+是对VFH的改进，VFH*又是对VFH+的改进。也就是下面这样的关系
$$VFF>>VFH>>VFH+>>VFH\ast$$
话不多说，直接上干货。

1、VFH+存在的问题——dead-end

VFH*之所以要改进VFH+，这是因为VFH+在某些情况下会出现很不希望出现的表现。请看下图，机器人检测到障碍物时，VFH+算法这个时候可以计算出两个可行的前进方向：A和B。VFH+这个时候是有很大的概率会选择A方向前进的。然而，很明显，如果机器人真的沿着A方向前进，那么很快机器人就会发现前方是一个dead-end（死胡同），机器人就不得不改变方向甚至原路返回后沿着B方向前进。

那我们就发现，这种情况下，机器人对待dead-end的表现是很差劲的。那我们就来分析一下，是什么导致机器人难以应对dead-end的呢？

不难发现，VFH+采用一个圆（实际上是传感器的数据，比如声呐）来检测障碍物，但是这一个圆的半径总归是有限的，这就导致机器人实际上能看到的视野也是十分有限的，那已知信息很少，自然控制效果也就比较差了。那么我们该采取什么手段来解决问题呢？

我们再来分析一下，VFH+之所以如此，是因为VFH+没有考虑如果真的沿着选择的方向前进后会遇到什么。如果他考虑了，那就有可能及早发现dead-end，从而尽早选择别的路。这就是VFH*算法。

2、VFH*算法

2.1 VFH*算法概述

VFH*所做的改进其实非常少，只有一步，那就是纳入了前瞻距离（Look-ahead），即通过提前探查一下如果真的沿着某一个方向前进会不会遇到dead-end，根据探查的结果，来选择更好的前进方向。

不过，虽然只是改进了一步，所做的工作却不少。下面我们来具体的描述一下这一个过程。

VFH*首先也是构建极坐标直方图，然后根据直方图中的openings来确定所有候选的前进方向。只不过VFH*在此时并不急于确定最终的前进方向，而是要沿着每一个方向进行探查。探查的过程类似于A*算法中的expansion操作。

假如说，机器人确定了N个候选的前进方向，那么以机器人的当前位置为根节点，沿着这N个前进方向进行探查。每一次探查的距离设置为$d_s$(这是探查阶段的第一个重要参数)，探查出来的新节点标记为projected node，然后计算该节点处的代价和启发函数值。然后，在新节点处继续探查。一直重复$n_g$次(这是VFH*算法的第二个重要的参数)。

在探查阶段完成之后，在搜索树中搜索那一条代价最短的路径。这一条路径VFH*算法规划出的避障路径。

2.1.1 VFH*的参数

总的说来，VFH*算法有三个主要的参数，$d_s$、$n_g$、$d_t$，并且这三者之间满足如下关系：
$$d_t=n_g\ast d_s$$

其中，$d_s$每一次探查的距离，建议设置为机器人的直径；$n_g$是设定的探查次数，一般设置为2；$d_t$总共探查的距离，最好接近机器人传感器的有效检测距离。

2.2.2 表示

VFH算法重点关注的是边的方向，因此我们的描述也把重点放在边上。

我们把机器人当前的位置记为primary node，把探查出来的节点记为projected node，它们有两个属性：position和orientation。

把在primary node处计算出的候选前进方向称为 primary candidate orientation。

把在projected node处计算出的候选前进方向称为 projected candidate orientation。

我们把每一个探查出来的边称为方向段。

2.2.3 算法步骤

VFH*算法在节点$i$处的探查总共分为5步：

1. 在节点$i$处，也就是projected position$(x_i,y_i)$构建极坐标直方图
2. 在直方图中确定所有的候选前进方向
3. 沿着所有的候选前进方向计算探查出来的新节点的位置和方向
4. 计算这些新节点的代价
5. 计算这些新节点的启发式距离。

前两步和VFH+完全一样，下面只介绍3-5步。

2.2 投影位置和方向

进行探查时探查出来的方向段，是用圆弧和直线来近似表示的。探查距离设置为$d_s$。
设置机器人向左转弯、向右转弯的最小转弯半径为$r_l$、$r_r$。其示意图如下图所示：

那么在沿着某一个候选前进方向探查时，首先判断机器人在投影距离内能不能到达到达这一方向。如果不能，那么投影轨迹就简单地用一个固定曲率的圆弧来代替。

区分向左探查和向右探查也是很有必要的，并且规定，允许向左、向右选择的方向范围应该在${\theta }_l$和${\theta }_r$之间，其中
$${\theta }_l={\theta }_i-d_s/r_l$$
$${\theta }_r={\theta }_i-d_s/r_r$$

说实话，作者的这一段描述，我是着实不理解。难道不就向着某一个方向新生长出来一个节点，然后在该节点处应用VFH+算法计算该点处的候选前进方向，然后计算代价函数并继续探查吗？怎么说的那么迷糊呢？

2.3 代价函数

在VFH+中使用的代价函数如下所示：

其中，第一项代表该方向和目标方向的差值；第二项代表该方向和机器人当前方向的差值；第三项代表该方向和上一次选择的方向之间的差值。如果希望VFH+是目标导向的，则需要满足${\mu }_1>{\mu }_2+{\mu }_3$。

在VFH*算法中，我们为每一个投影出的候选方向（方向段）计算代价，采用如下函数

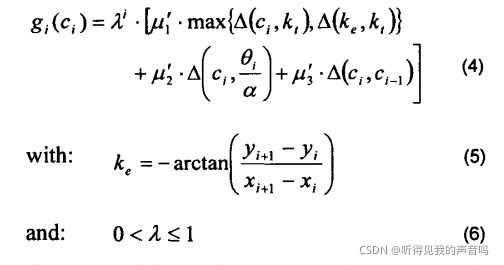
2.3.1 $k_e$项

(4)的第一项依然是代表目标导向。但是这个函数和VFH+用到的函数略有不同，在某一个projected node处，我们计算它的代价时不仅考虑了目标方向，还引入了另一项，那就是$k_e$，称为forward progress，这一项代表从该节点的父节点到该节点处的方向角，那么为什么要引入这一项呢？请看下图。

在每一个projected node处，候选前进方向都是和目标方向一致的，但是我们发现，节点的expansion却是在一个圆弧上，并不是靠近目标的，所以仅仅考虑该节点处的方向，不足以评价该节点的好坏，因此需要引入另一项，也就是$k_e$，该项代表该节点是靠近目标了还是远离目标了，因而可以更好的评价一个节点趋向目标点的程度。

值得强调的是，只有在计算连接projected node及其父节点的那一个方向段的代价时，才会考虑$k_e$，在计算机器人primary node处的方向段时不考虑$k_e$项。

2.3.2 平滑项

代价函数的第二项和第三项是用来决定机器人运动平滑程度的。为了保证机器人的目标导向性，需要满足
$${\mu }_1’>{\mu }_2’+{\mu }_3^{’}$$
同时为了强调primary 候选方向的重要性，需要满足
$${\mu }_1>{\mu }_1^{’}$$

2.3.3 折扣因子λ

代价函数中另一个很重要的因子是λ，该因子是基于这样的考虑，探查的越远，那么该处的节点对机器人的避障影响就越小，因此随着探查的深入，相应的代价也随之减小。
那如果我们不设置这一个折扣因子，会发生什么事？请看下图。

上图中，有A、B、C三条路径，如果不设置折扣因子（等同于把折扣因子设置为1），那么搜索阶段搜索到的代价最低的路径将会是B。为什么呀？直观看来明显应该是A比B更好呀。这是因为没有折扣因子的话，每一个方向段对代价的影响是相同的，很明显B在最后几次探查中，一直和目标方向一致，导致其代价比较小，因而B的代价就比A小了。而在引入折扣因子之后，就强化了离机器人较近的方向段，削弱了离机器人较远的方向段。这个时候，A就可以战胜B成为代价最小的路径了。

另外，上图中的探查次数$n_g$为7。我们可以发现，只要$n_g$再大一，B就会检测到障碍物，从而B的代价就会急剧增加。但是此时我们很可能依然无法判定A，因为此时，C依然是没有碰到障碍物，很可能C的代价还是比A小，我们依然没办法把A这一条我们期望的路径给挑出来。这说明仅仅通过调整探查深度$n_g$是没有办法达到目的的。必须通过这一个折扣因子λ才能够实现。

2.4 启发函数

启发式函数是用来评价这一个projected node 距离目标远近程度的，可以帮助算法更快地收敛。最简单的一个启发函数为

可以看得出来上面这个启发函数直接用$k_t$来代替$c_0$。这个函数只考虑了机器人当时的方向和前一节点处的方向，而没有考虑$k_e$。

我们可以选择一个更好的启发函数：
这一个函数考虑了$k_e$的影响，但是代价就是其计算量大了。

2.5 枝叶因子b

为了加快搜索阶段的执行效率，我们才可采取修剪搜索树的方法。

每一个projected node在扩展之后，都会有几个successor node，successor node的数量和这一个节点的候选前进方向的数量是一致的。我们一般将探查距离$d_s$设置为机器人的直径，这个值对于机器人所处的环境来说通常是很小的。因而这些新扩展出来的节点是很接近的，我们不妨把它们看成一个节点。

并且，我们在前面确定过机器人可以向左、向右制动的最大方向角。
$${\theta }_l={\theta }_i-d_s/r_l$$
$${\theta }_r={\theta }_i-d_s/r_r$$
那么所有那些，超过了这一个范围的新节点，都给整合成一个节点。并且在机器人的左侧方向和右侧方向我们均尽量只保留一枝，这样的话，一个节点的successor node个数很少会超过3。

最后我们在这一个树中搜寻代价最小的“枝”，这就是我们期望的那一条路径。

3、算法分析

我觉得这个算法思路是很好的。只是$n_g$这一个参数有些难整。
作者说，$n_g$设置的小一些，算法速度更快，但是处理dead-end的能力也较弱。$n_g$越大，处理dead-end的能力越强，但是计算量就大大增加。
并且作者说，$n_g$设置为2可以应对绝大多数情况。