MATLAB 画图总结小技巧-1：预设符号变量类型2：if 转 switch (逻辑值作为输入变量)3：matlab 拟合曲线后转换成匿名函数4：更快的查看每个模块包含的函数

1：预设符号变量类型

假设我们编写了如下代码：

syms x
f=x^3+x^2+9*x+9;
solve(f==0)

 此时求解结果为：

ans =
 
  -1
 -3i
  3i

但如果在求解前预设x为实数：

ans =
 
-1

 其他预设

Assume ‘x’ is	Syntax
real	assume(x,'real')
rational	assume(x,'rational')
positive	assume(x,'positive')
positive integer	assume(x,{'positive','integer'})
less than -1 or greater than 1	assume(x<-1)
an integer from 2 through 10	assume(in(x,'integer') & x>2 & x<10)
not an integer	assume(~in(z,'integer'))
not equal to 0	assume(x ~= 0)
even	assume(x/2,'integer')
odd	assume((x-1)/2,'integer')
from 0 through 2π	assume(x>0 & x<2*pi)
a multiple of π	assume(x/pi,'integer')

2：if 转 switch (逻辑值作为输入变量)

假如你编写了如下代码：

score=68
if 90<=score&&score<=100
    disp('优秀');
elseif 70<=score&&score<90
    disp('良好');
elseif 60<=score&&score<70
    disp('一般');
elseif score<60
    disp('不及格');
end

有个办法能够避免大量 if else：

就是拿逻辑值作为输入使用 switch:

score=68
switch true
    case 90<=score&&score<=100
        disp('优秀');
    case 70<=score&&score<90
        disp('良好');
    case 60<=score&&score<70
        disp('一般');
    case score<60
        disp('不及格');
end

 输出结果

score =

    68

一般

3：matlab 拟合曲线后转换成匿名函数

x=[2 2.5 3 3.5 4 4.5 5 5.5 6];
y=[41 38 34 32 29 28 25 22 20];
p=polyfit(x,y,3);
f=matlabFunction(poly2sym(p))

xx=2:.1:6;
plot(xx,f(xx),'LineWidth',2)
grid on

f =

  包含以下值的 function_handle:

    @(x)x.*(-8.57e+2./5.4e+1)+x.^2.*(2.56e+2./9.9e+1)-x.^3.*(5.8e+1./2.97e+2)+7.05e+2./1.1e+1

4：更快的查看每个模块包含的函数

我点开这个小三角，这个三角也太细节了叭hiahiahia，点开后会出现一个像电子词典样子的help文档合集:

5：sub2ind及ind2sub

假设我们要把全零矩阵第(2,3)个元素及第(3,2)个元素变为1，如果编写了如下代码：

A=zeros(4,4);
A([2,3],[3,2])=1

A =

     0     0     0     0

     0     1     1     0

     0     1     1     0

     0     0     0     0

我们会发现不只改变了两个元素，但我们可以通过sub2ind函数将双变量索引改为单变量索引，例如([4,4]为矩阵尺寸)：

A=zeros(4,4);
A(sub2ind([4,4],[2,3],[3,2]))=1

A =

     0     0     0     0

     0     0     1     0

     0     1     0     0

     0     0     0     0

ind2sub函数可以用来减少循环嵌套次数，举个简单的例子，假如编写了如下代码：

for i1=1:5
    for i2=1:3
        for i3=1:2
            disp([i1,i2,i3])
        end
    end
end

可以改写为如下代码(用处不多且需要注意顺序，远没上一条重要)：

sz=[5,3,2];
for i=1:prod(sz)
    [i3,i2,i1]=ind2sub(sz(end:-1:1),i);
    disp([i1,i2,i3])
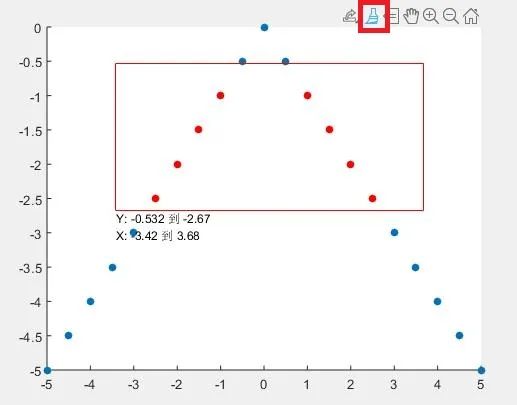
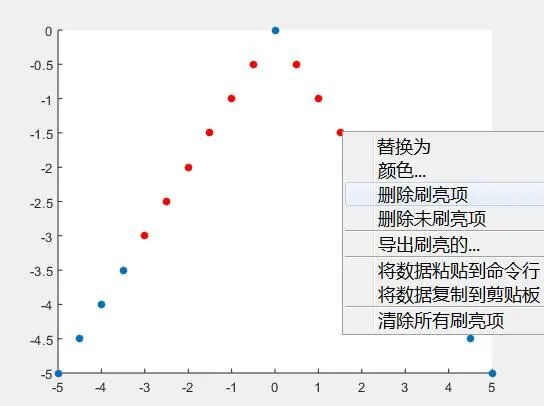
end

6：刷亮数据

不会有人还没点过这个小刷子叭：

点击后可以将部分数据刷亮，之后右键点击被刷亮的数据，可以把数据导出，换颜色，或者直接把数据删掉，交互式绘图大杀器有没有：

7：大小为0的矩阵

就比如我要创建一个[x1,y1;x2,y2;x3,y3;... ...]这样的矩阵，每一轮往最后加入新点，但每次加入点的个数未知，要添加次数也未知，我们就不如创建一个0xn大小的矩阵不断的往后面增添新的元素：

% 创建0行2列矩阵
P=zeros(0,2);
% 循环随机5-10之间的随机轮
for i=1:randi([5,10],[1,1]) 
    % 每次随机增加2-5行随机数
    P=[P;rand(randi([2,5],[1,1]),2)]
end

8：任意进制相互转换

就是先转成十进制，再转换为其他进制：

% 12进制转16进制
bs1=12;
bs2=16;
% 原字符
baseStr='1B';

% 转换
decStr=base2dec(baseStr,bs1);
result=dec2base(decStr,bs2)
% result='17'

因此有更简单的RGB颜色、16进制码相互转换函数:

RGB值转16进制码函数：

function HEX=RGB2HEX(RGB)
    hexVec=dec2base(RGB,16)';
    HEX=['#',hexVec(:)'];
end

调用：

hex=RGB2HEX([251,255,250])
% hex = '#FBFFFA' 

16进制码转RGB值函数：

function RGB=HEX2RGB(HEX)
    hexVec=reshape(HEX(2:end),2,[])';
    RGB=base2dec(hexVec,16)';
end

调用：

rgb=HEX2RGB('#FBFFFA')
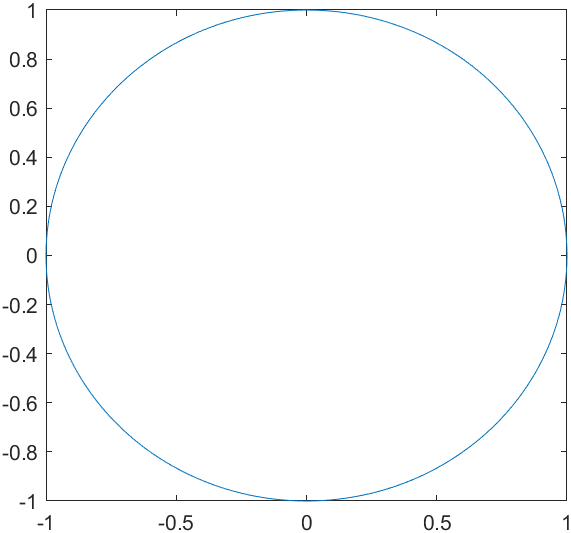
% rgb = [251,255,250]

9：虚平面绘图

MATLAB 支持虚平面绘图，就是实部对应X轴坐标，虚部对应Y轴坐标，使用虚平面绘图可以只使用一个数组便绘制隐函数，举个例子，使用虚平面绘图绘制圆形：

t=0:pi/100:2*pi;
plot(exp(t.*1i))

10：MATLAB高精度计算

一般MATLAB中如果两个数的数值相差小于eps，则认为数值相同，例如以下两个判断MATLAB都会认为是对的：

1==1+eps/2
1==1+1e-20

ans =

logical

   1

ans =

logical

   1

eps的数值为2.2204e-16，只要我们将精度设置的更高就不会出现上述问题，例如：

digits(50)
logical(vpa(1)==vpa(1)+vpa(1e-20))

ans =

logical

   0

再比如，我想显示圆周率的前100位小数：

digits(100)
pi100=vpa(pi)

pi100=3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068