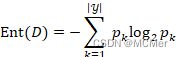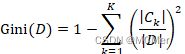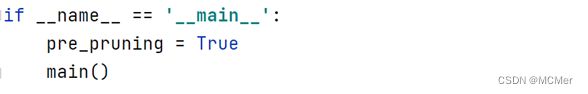西瓜书学习笔记---第四章 决策树

目录

一、题目要求

二、数据集介绍

 三、决策树模型

3.1 决策树模型介绍

3.2 决策树算法原理

3.2.1 决策树的建立

3.2.2 决策树的划分（1）—信息增益ID3

3.2.3 决策树的划分（2）—Gini指数CART

3.2.4 预剪枝pre-pruning

3.2.5 后剪枝post-pruning

3.3 决策树算法核心代码解释

四、运行结果

五、附件（见我的资源）

---

一、题目要求

4.3  编程实现基于信息熵进行划分选择的决策树算法，并为西瓜数据集3.0中的数据生成一颗决策树。

4.4 编程实现基于基尼指数进行划分选择的决策树算法，为西瓜数据集2.0生成预剪枝、后剪枝决策树，并与未剪枝决策树进行比较。

4.6 选择4个UCI数据集，对上述2种算法产生的未剪枝，预剪枝，后剪枝的决策树进行实验比较，并进行适当的统计显著性检验。

二、数据集介绍

        本次实验使用到三个数据集，分别是西瓜数据集2.0 ，西瓜数据集3.0，UCI分类数据集中的糖尿病数据集“Diabetes.xls”和乳腺癌数据集“breast_cancer.csv”。

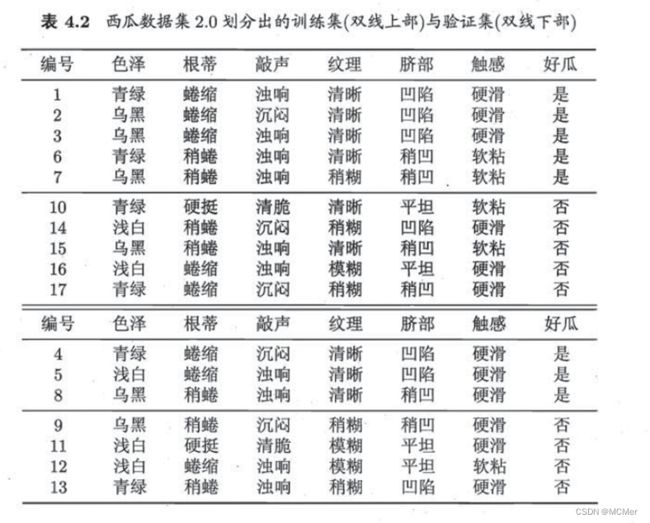
        西瓜数据集2.0包含17条信息，每条信息对应西瓜的6种属性（色泽、根蒂、敲声、纹理、脐部、触感），给出了该西瓜是否为好瓜，“是”表示该西瓜是好瓜，“否”表该西瓜不是好瓜。西瓜数据集2.0分为训练集和验证集两部分，其中训练集10条数据，验证集7条数据。西瓜数据集2.0的具体内容如下图所示。

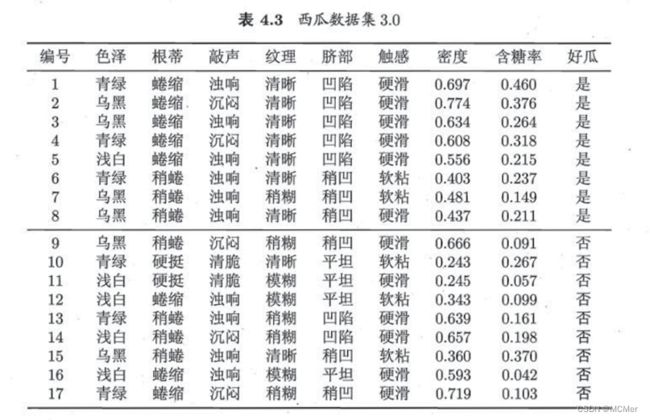
        西瓜数据集3.0包含17条信息，是对西瓜数据集2.0的扩展，在原来的基础上增加两个连续属性“密度”和“含糖率”。每条信息对应西瓜的8种属性（色泽、根蒂、敲声、纹理、脐部、触感、密度、含糖率），给出了该西瓜是否为好瓜，“是”表示该西瓜是好瓜，“否”表该西瓜不是好瓜。西瓜数据集3.0的具体内容如下图所示。

        鸢尾花“Iris”数据集共包含150条信息，每条信息对应鸢尾花的4种属性（花萼长度，花萼宽度，花瓣长度，花瓣宽度）均为连续变量，并给出了该鸢尾花的分类（setosa，virginica，versicolor）。

        气球“Balloons Data”数据集共包含20条信息，每条信息对应4种属性（color，size，act，age）均为离散变量，并给出了判断结果T,F。

        红酒“Wine”数据集共包含178条信息，每条信息对应红酒的13种属性（Alcohol, Malic acid, Ash, Alcalinity of ash, Magnesium, Total phenols，Flavanoids，Nonflavanoid phenols，Proanthocyanins，Color intensity，Hue，OD280/OD315 of diluted wines，Proline）均为连续变量，并给出了该红酒的分类（wine_1, wine_2, wine_3）。

 三、决策树模型

3.1 决策树模型介绍

        决策树是经典的分类模型，常用于二分类。决策树通过监督学习的方式生成一个树形结构，其中每个内部节点表示一个属性上的判断，每个分支代表一个判断结果的输出，最后每个叶节点代表一种分类结果。

        每次都找不同的切分点，将样本空间逐渐进行细分，最后把属于同一类的空间进行合并，就形成了决策边界，树的层次越深，决策边界的切分就越细，区分越准确，同时也越有可能产生过拟合。

        决策树学习算法主要由三部分构成：特征选择，决策树生成，决策树剪枝。

3.2 决策树算法原理

3.2.1 决策树的建立

        决策树的建立遵循如下流程：

         决策树的生成是一个递归过程，在决策树基本算法中，有三种情形会导致递归返回：（1）当前结点包含的样本完全属于同一类别，无需划分；（2）当前属性集为空，或是所有样本在所有属性上取值相同，无法划分；（3）当前结点包含的样本集为空，不能划分。

3.2.2 决策树的划分（1）—信息增益ID3

·信息熵(Entropy)

        信息熵(Entropy) 是度量样本集合纯度最常用的一种指标，假定当前样本集合D中第k类样本所占的比例为，则D的信息熵定义为：

        的值越小，则D的纯度越高，其中若，则定义。

        离散属性有V个可能的取值，用来进行划分，则会产生V个分支结点，其中第个分支结点包含了D中所有在属性a上取值为的样本，记为。则可计算出用属性对样本集D进行划分所获得的“信息增益”:

        一般而言，信息增益越大，则意味着使用属性a来进行划分所获得的“纯度提升”越大。ID3决策树学习算法以信息增益为准则来选择划分属性。ID3算法的核心是在决策树的各个结点上应用信息增益准则进行特征选择。具体做法是：

• · 从根节点开始，对结点计算所有可能特征的信息增益，选择信息增益最大的特征作为结点的特征，并由该特征的不同取值构建子节点；
• · 对子节点递归地调用以上方法，构建决策树；
• · 直到所有特征的信息增益均很小或者没有特征可选时为止。

• 判断数据集中的每个子项是否属于同一类：

• 判断数据集中的每个子项是否属于同一类：     if true:         return 类标签；     else:         寻找划分数据集的最佳特征         根据最佳特征划分数据集         创建分支节点         for 每个划分的子集             递归调用createBranch();         return 分支节点

   

  3.2.3 决策树的划分（2）—Gini指数CART

•        CART与ID3区别： CART中用于选择变量的不纯性度量是Gini指数； 如果目标变量是标称的，并且是具有两个以上的类别，则CART可能考虑将目标类别合并成两个超类别（双化）； 如果目标变量是连续的，则CART算法找出一组基于树的回归方程来预测目标变量。

  •         Gini 指数

           分类问题中假设有K个类，样本点属于第 k个类的概率为pk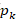，则概率分布的基尼指数为定义为：

    

           对于二分类问题和给定的样本集合D其基尼指数为:

    

           若样本集合D根据特征A是否取某一可能的值a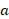分割为D1,D2两部分，则在特征A的条件下集合D的基尼指数定义为:

    

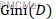            反映了数据集D的纯度，值越小，纯度越高。我们在候选集合中选择使得划分后基尼指数最小的属性作为最优化分属性。

           CART是一棵二叉树，采用二元切分法，每次把数据切成两份，分别进入左子树、右子树。而且每个非叶子节点都有两个孩子，所以CART的叶子节点比非叶子多1。相比ID3和C4.5，CART应用要多一些，既可以用于分类也可以用于回归。CART分类时，使用基尼指数（Gini）来选择最好的数据分割的特征，gini描述的是纯度，与信息熵的含义相似。CART中每一次迭代都会降低GINI系数。

    算法流程： 1. CART回归树预测回归连续型数据，假设X与Y分别是输入和输出变量，并且Y是连续变量。在训练数据集所在的输入空间中，递归的将每个区域划分为两个子区域并决定每个子区域上的输出值，构建二叉决策树。 2. 选择最优切分变量j与切分点s：遍历变量j，对规定的切分变量j扫描切分点s，选择使下式得到最小值时的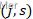对。其中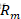是被划分的输入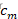空间，是空间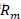对应的固定输出值。 3. 用选定的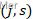对，划分区域并决定相应的输出值。 4. 继续对两个子区域调用上述步骤，将输入空间划分为M个区域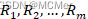,生成决策树。

• 3.2.4 预剪枝pre-pruning

  •         预剪枝就是在树的构建过程（只用到训练集），设置一个阈值（样本个数小于预定阈值或GINI指数小于预定阈值），使得当在当前分裂节点中分裂前和分裂后的误差超过这个阈值则分列，否则不进行分裂操作。所有决策树的构建方法，都是在无法进一步降低熵的情况下才会停止创建分支的过程，为了避免过拟合，可以设定一个阈值，熵减小的数量小于这个阈值，即使还可以继续降低熵，也停止继续创建分支。但是这种方法实际中的效果并不好。

            在划分之前，所有样本集中于根节点，若不进行划分，该节点被标记为叶节点，其类别标记为训练样例最多的类别。若进行划分在测试集上的准确率小于在根节点不进行划分的准确率，或增幅没有超过阈值，都不进行划分，作为一个叶节点返回当前数据集中最多的标签类型。

            优点：快速，可以在构建决策树时进行剪枝，显著降低了过拟合风险。由于预剪枝不必生成整棵决策树，且算法相对简单，效率很高，适合解决大规模问题。但是尽管这一方法看起来很直接， 但是怎样精确地估计何时停止树的增长是相当困难的。

            缺点：预剪枝基于贪心思想，本质上禁止分支展开，给决策树带来了欠拟合的风险。因为视野效果问题。也就是说在相同的标准下，也许当前的扩展会造成过度拟合训练数据，但是更进一步的扩展能够满足要求，也有可能准确地拟合训练数据。这将使得算法过早地停止决策树的构造。

  • 3.2.5 后剪枝post-pruning

    •         决策树构造完成后进行剪枝。剪枝的过程是对拥有同样父节点的一组节点进行检查，判断如果将其合并，熵的增加量是否小于某一阈值。如果确实小，则这一组节点可以合并一个节点，其中包含了所有可能的结果。后剪枝是目前最普遍的做法。

              后剪枝的剪枝过程是删除一些子树，然后用其叶子节点代替，这个叶子节点所标识的类别通过大多数原则(majority class criterion)确定。所谓大多数原则，是指剪枝过程中, 将一些子树删除而用叶节点代替,这个叶节点所标识的类别用这棵子树中大多数训练样本所属的类别来标识。相比于前剪枝，后剪枝方法更常用，是因为在前剪枝方法中精确地估计何时停止树增长很困难。

              优点：欠拟合风险小，泛化性能好。

              缺点：在生成决策树之后完成，自底向上对所有非叶节点进行逐一考察，训练的时间开销较大。

    • 3.3 决策树算法核心代码解释

    • 1. 离散数据集划分

    • def split_discrete_dataset(dataset, feature_index, value):
      # dataset:待划分集合, feature_index:指示划分所依据的属性, value:该属性用于划分的取值
          dataset_out = []  # 为return dataset 返回一个列表
          for featVec in dataset:  # 抽取符合条件的特征值
              if featVec[feature_index] == value:
                  reduced_feat = featVec[:feature_index]  # 该特征之前的特征仍然保留在dataset中
                  reduced_feat.extend(featVec[feature_index + 1:])  # 该特征之后的特征仍然保留在样本中
                  dataset_out.append(reduced_feat)  # 把去除掉feature_index特征的样本加入到list
          return dataset_out
      

      2. 连续数据集划分

    • def split_continuous_dataset(dataset, feature_index, value):
          dataset_out_0 = []
          dataset_out_1 = []
          for featVec in dataset:
              if featVec[feature_index] > value:
                  reduced_feat_1 = featVec[:feature_index]  # 该特征之前的特征仍然保留在dataset中
                  reduced_feat_1.extend(featVec[feature_index + 1:])  # 该特征之后的特征仍然保留在样本中
                  dataset_out_1.append(reduced_feat_1)
              else:
                  reduced_feat_0 = featVec[:feature_index]  # 该特征之后的特征仍然保留在dataset中
                  reduced_feat_0.extend(featVec[feature_index + 1:])  # 该特征之后的特征仍然保留在样本中
                  dataset_out_0.append(reduced_feat_0)
          return dataset_out_0, dataset_out_1  # 返回两个集合，分别为大于和小于该value
      

      3. ID3算法实现

      •         ID3算法核心有三部分，一分别是信息熵的计算，按照信息增益选取最优特征，已及ID3决策树的生成。

      • # 计算数据集的信息熵(Information Ent)
        def calc_InfoEnt(dataset):  # dataset每一列是一个属性(列末是label)
            num_entries = len(dataset)  # dataset每一行是一个样本
            label_counts = {}  # 给所有可能的分类创建字典label_counts
            for featVec in dataset:  # 按行循环
                current_label = featVec[-1]  # featVec的最后一个值为label
                if current_label not in label_counts.keys():  # 如果当前label还未在字典中出现
                    label_counts[current_label] = 0  # 创建该label的key
                label_counts[current_label] += 1  # 统计每一类label的数量
            InfoEnt = 0.0  # 初始化InfoEnt信息熵的值
            for key in label_counts:
                p = float(label_counts[key]) / num_entries  # 求出每一类label的概率
                InfoEnt -= p * np.math.log(p, 2)  # 信息熵计算公式
            return InfoEnt
        

        # 根据InfoGain选择当前最好的划分特征(以及对于连续变量还要选择以什么值划分)
        def ID3_best_split(dataset, label):
            feat_num = len(dataset[0]) - 1  # 根据dataset判断要划分的特征的数量
            base_Ent = calc_InfoEnt(dataset)  # 计算初始Ent
            best_infoGain = 0.0  # 初始化信息增益率
            best_feature = -1
            best_split = -1
            best_split_dict = {}
            for i in range(feat_num):
                # 遍历所有特征：取每一行的第i个，即得当前集合所有样本第i个feature的值
                feat_list = [example[i] for example in dataset]
                # 判断是否为离散特征
                if not (type(feat_list[0]).__name__ == 'float' or type(feat_list[0]).__name__ == 'int'):
                    # 对于离散特征：求若以该特征划分的增熵
                    unique_vals = set(feat_list)  # 从列表中创建集合set(获得得列表唯一元素值)
                    new_Ent = 0.0
                    for value in unique_vals:  # 遍历该离散特征每个取值
                        sub_dataset = split_discrete_dataset(dataset, i, value)  # 计算每个取值的熵
                        p = len(sub_dataset) / float(len(dataset))
                        new_Ent += p * calc_InfoEnt(sub_dataset)  # 各取值的熵累加
                    infoGain = base_Ent - new_Ent  # 得到以该特征划分的熵增
                    print(u"ID3中第%d个特征的信息增益为：%.3f" % (i, infoGain))
                    # 对于连续特征：求若以该特征划分的增熵(n个数据需要添加n-1个候选划分点，并选择最佳划分点)
                else:
                    # 产生n-1个候选划分点
                    sort_feat_list = sorted(feat_list)
                    split_list = []
                    for j in range(len(sort_feat_list) - 1):  # 产生n-1个候选划分点
                        split_list.append(round(((sort_feat_list[j] + sort_feat_list[j + 1]) / 2.0), 3))
                    best_split_Ent = 10000
                    # 遍历n-1个候选划分点：求第j个候选划分点划分时的增熵，并选择最佳划分点
                    for j in range(len(split_list)):
                        value = split_list[j]
                        new_Ent = 0.0
                        new_dataset = split_continuous_dataset(dataset, i, value)
                        sub_dataset_0 = new_dataset[0]
                        sub_dataset_1 = new_dataset[1]
                        p0 = len(sub_dataset_0) / float(len(dataset))
                        new_Ent += p0 * calc_InfoEnt(sub_dataset_0)
                        p1 = len(sub_dataset_1) / float(len(dataset))
                        new_Ent += p1 * calc_InfoEnt(sub_dataset_1)
                        if new_Ent < best_split_Ent:
                            best_split_Ent = new_Ent
                            best_split = j
                    best_split_dict[label[i]] = split_list[best_split]  # 字典记录当前连续属性的最佳划分点
                    infoGain = base_Ent - best_split_Ent  # 计算以该节点划分的熵增
                    print(u"ID3中第%d个特征的信息增益为：%.3f" % (i, infoGain))
                # 在所有属性(包括连续和离散)中选择可以获得最大熵增的属性
                if infoGain > best_infoGain:
                    best_infoGain = infoGain
                    best_feature = i
            # 若当前节点的最佳划分特征为连续特征，则需根据“是否小于等于其最佳划分点”进行二值化处理
            if type(dataset[0][best_feature]).__name__ == 'float' or \
                    type(dataset[0][best_feature]).__name__ == 'int':
                best_split_value = best_split_dict[label[best_feature]]
                label[best_feature] = label[best_feature] + '<=' + str(best_split_value)
                for i in range(np.shape(dataset)[0]):
                    if dataset[i][best_feature] <= best_split_value:
                        dataset[i][best_feature] = 1
                    else:
                        dataset[i][best_feature] = 0
            return best_feature
        

        # 递归产生决策树
        def ID3_createTree(dataset, labels, data_full, labels_full, data_test):
            class_list = [example[-1] for example in dataset]
            if class_list.count(class_list[0]) == len(class_list):
                # 类别完全相同，停止划分
                return class_list[0]
            if len(dataset[0]) == 1:
                # 遍历完所有特征时返回出现次数最多的
                return majorityCnt(class_list)
            temp_labels = copy.deepcopy(labels)
            best_feat = ID3_best_split(dataset, labels)
            best_featLabel = labels[best_feat]
            print(u"此时最优索引为：" + best_featLabel)
            ID3_Tree = {best_featLabel: {}}
            feat_values = [example[best_feat] for example in dataset]
            unique_vals = set(feat_values)
            unique_vals_full = set()
            if type(dataset[0][best_feat]).__name__ == 'str':
                current_label = labels_full.index(labels[best_feat])
                feat_values_full = [example[current_label] for example in data_full]
                unique_vals_full = set(feat_values_full)
            del (labels[best_feat])  # 划分完后, 即当前特征已经使用过了, 故将其从“待划分特征集”中删去
            # 针对当前用于划分的特征(beat_Feat)的每个取值，划分出一个子树
            for value in unique_vals:  # 遍历该特征余下的取值
                sub_labels = labels[:]
                if type(dataset[0][best_feat]).__name__ == 'str':
                    unique_vals_full.remove(value)  # 划分后删去
                ID3_Tree[best_featLabel][value] = ID3_createTree(split_discrete_dataset(dataset, best_feat, value), sub_labels,
                                                                 data_full, labels_full, data_test)
            # 连续特征在划分后处理成离散取值
            if type(dataset[0][best_feat]).__name__ == 'str':
                for value in unique_vals_full:
                    # 因为那些现有数据集中没取到的该特征的值，保留在了其中
                    ID3_Tree[best_featLabel][value] = majorityCnt(class_list)
            if pre_pruning is True:
                if tree_acc(ID3_Tree, data_test, temp_labels) >= major_acc(majorityCnt(class_list), data_test):
                    return majorityCnt(class_list)
        
            return ID3_Tree
        

        4. CART算法实现

        •         CART算法核心有三部分，一分别是Gini值的计算，按照Gini选取最优特征，已及CART决策树的生成。

        • # Gini值的计算
          for i in range(feat_num):
                  # 遍历所有特征：取每一行的第i个，即得当前集合所有样本第i个feature的值
                  feat_list = [example[i] for example in dataset]
                  unique_vals = set(feat_list)  # 从列表中创建集合set(获得得列表唯一元素值)
                  gini = 0.0
                  for value in unique_vals:
                      sub_dataset = split_discrete_dataset(dataset, i, value)  # 计算每个取值的熵
                      p = len(sub_dataset) / float(len(dataset))
                      sub_p = len(split_discrete_dataset(sub_dataset, -1, '坏瓜')) / float(len(sub_dataset))
                      gini += 2 * p * sub_p * (1 - sub_p)
                  # print(u"CART中第%d个特征的基尼值为：%.3f" % (i, gini))
          

          # 根据Gini选择当前最好的划分特征
          def CART_best_split(dataset):
              feat_num = len(dataset[0]) - 1  # 根据dataset判断要划分的特征的数量
              best_Gini = 99999.0  # 初始化Gini指数
              best_feature = -1
              for i in range(feat_num):
                  # 遍历所有特征：取每一行的第i个，即得当前集合所有样本第i个feature的值
                  feat_list = [example[i] for example in dataset]
                  unique_vals = set(feat_list)  # 从列表中创建集合set(获得得列表唯一元素值)
                  gini = 0.0
                  for value in unique_vals:
                      sub_dataset = split_discrete_dataset(dataset, i, value)  # 计算每个取值的熵
                      p = len(sub_dataset) / float(len(dataset))
                      sub_p = len(split_discrete_dataset(sub_dataset, -1, '坏瓜')) / float(len(sub_dataset))
                      gini += 2 * p * sub_p * (1 - sub_p)
                  # print(u"CART中第%d个特征的基尼值为：%.3f" % (i, gini))
                  if gini < best_Gini:
                      best_Gini = gini
                      best_feature = i
              return best_feature
          

          # 生成CRAT决策树
          def CART_creatTree(dataset, labels, test_dataset):
              class_list = [example[-1] for example in dataset]
              if class_list.count(class_list[0]) == len(class_list):
                  # 类别完全相同，停止划分
                  return class_list[0]
              if len(dataset[0]) == 1:
                  # 遍历完所有特征时返回出现次数最多的
                  return majorityCnt(class_list)
              best_feat = CART_best_split(dataset)
              best_featLabel = labels[best_feat]
              print(u"此时最优索引为：" + best_featLabel)
              CART_Tree = {best_featLabel: {}}
              del (labels[best_feat])
              # 得到列表包括节点所有的属性值
              feat_values = [example[best_feat] for example in dataset]
              unique_vals = set(feat_values)
          
              if pre_pruning is True:
                  ans = []
                  for index in range(len(test_dataset)):
                      ans.append(test_dataset[index][-1])
                  result_counter = Counter()
                  for vec in dataset:
                      result_counter[vec[-1]] += 1
                  leaf_output = result_counter.most_common(1)[0][0]
                  root_acc = cal_acc(test_output=[leaf_output] * len(test_dataset), label=ans)
                  outputs = []
                  ans = []
                  for value in unique_vals:
                      cut_testSet = split_discrete_dataset(test_dataset, best_feat, value)
                      cut_dataSet = split_discrete_dataset(dataset, best_feat, value)
                      for vec in cut_testSet:
                          ans.append(vec[-1])
                      result_counter = Counter()
                      for vec in cut_dataSet:
                          result_counter[vec[-1]] += 1
                      leaf_output = result_counter.most_common(1)[0][0]
                      outputs += [leaf_output] * len(cut_testSet)
                  cut_acc = cal_acc(test_output=outputs, label=ans)
          
                  if cut_acc <= root_acc:
                      return leaf_output
          
              # 【递归调用】针对当前用于划分的特征(beat_Feat)的每个取值，划分出一个子树
              for value in unique_vals:  # 遍历该特征【现存的】取值
                  sub_labels = labels[:]
                  CART_Tree[best_featLabel][value] = CART_creatTree(split_discrete_dataset(dataset, best_feat, value),
                                                                    sub_labels,
                                                                    split_discrete_dataset(test_dataset, best_feat, value))
          
              return CART_Tree
          

          5. 预剪枝算法实现

          •         预剪枝算法实现较为简单，就是在决策树划分过程加以判断，判断若进行划分在测试集上的准确率小于在根节点不进行划分的准确率，作为一个叶节点返回当前数据集中最多的标签类型。

            •     if pre_pruning is True:
                      if tree_acc(ID3_Tree, data_test, temp_labels) >= major_acc(majorityCnt(class_list), data_test):
                          return majorityCnt(class_list)
              

              6. 后剪枝算法实现

                      后剪枝算法相对复杂，剪枝的过程是对拥有同样父节点的一组节点进行检查，判断如果将其合并，准确率是否提高。如果提高，则这一组节点可以合并一个节点，其中包含了所有可能的结果。

              • def post_pruning(input_tree, dataset, data_test, labels):
                    first_str = list(input_tree.keys())[0]
                    second_dict = input_tree[first_str]
                    class_list = [example[-1] for example in dataset]
                    feat_key = copy.deepcopy(first_str)
                    label_index = labels.index(feat_key)
                    temp_labels = copy.deepcopy(labels)
                    del(labels[label_index])
                    for key in second_dict.keys():
                        if type(second_dict[key]).__name__ == 'dict':
                            if type(dataset[0][label_index]).__name__ == 'str':
                                input_tree[first_str][key] = post_pruning(second_dict[key],
                                                                          split_discrete_dataset(dataset, label_index, key),
                                                                          split_discrete_dataset(data_test, label_index, key),
                                                                          copy.deepcopy(labels))
                
                    if tree_acc(input_tree, data_test, temp_labels) <= major_acc(majorityCnt(class_list), data_test):
                        return input_tree
                    return majorityCnt(class_list)
                

                7. 决策树可视化

                        决策树采用字典的方式进行建立，但是字典可视效果较差，因此需要对决策树字典进行可视化处理。由于可视化部分并不是本章的重点，因此参考了网上广泛采用的plotTree.py文件进行决策树可视化，利用matplotlib库生成图形，详情可见附录。

              • 四、运行结果

                • 习题4.3

                       编程实现基于信息熵进行划分选择的决策树算法，并为西瓜数据集3.0中的数据生成一颗决策树。

                • 代码参见附录1，ID3.py生成ID3决策树的流程如下图所示：

                • 

                   生成的决策树如下所示：

                • 

                  • 习题4.4

                            编程实现基于基尼指数进行划分选择的决策树算法，为西瓜数据集2.0生成预剪枝、后剪枝决策树，并与未剪枝决策树进行比较。

                  • 代码参见附录2，CART_剪枝.py

                  • 生成CART未剪枝决策树的流程如下图所示：

                  • 

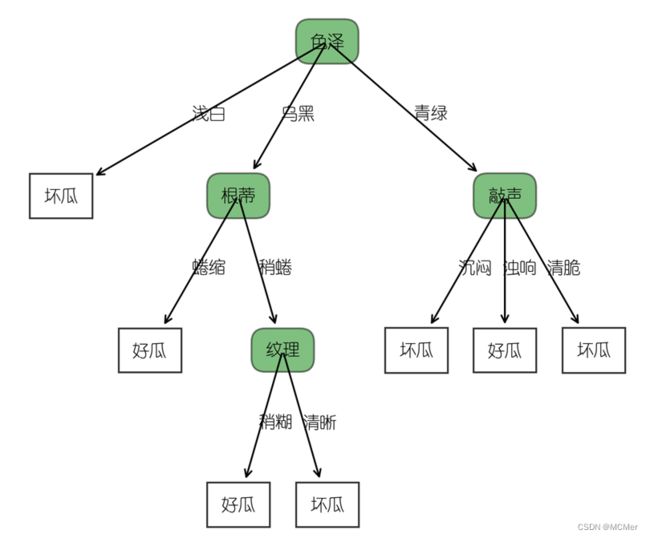
                     生成的未剪枝CART决策树如下所示：

                  • 

                     通过pre_pruning标志位来控制是否进行预剪枝操作

                  • 

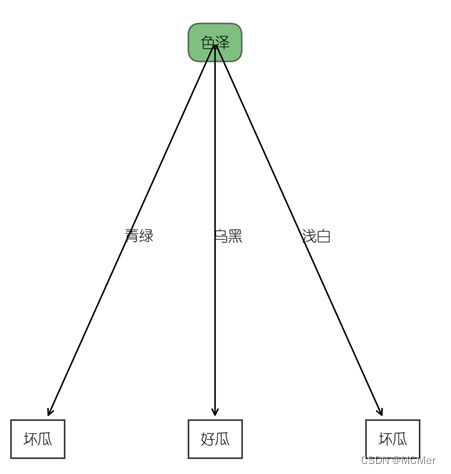
                     生成的预剪枝决策树如下所示：

                  • 

                    通过加载post_pruning()函数，来进行后剪枝操作

                    生成的后剪枝决策树如下所示：

                  • 

                    •         对比未剪枝、预剪枝和后剪枝生成的决策树，可以看出经过剪枝操作后决策树明显精简，其中后剪枝剪去了敲声和纹理两个内部结点，预剪枝减去色泽结点以外的所有结点。预剪枝比较快速，可以在构建决策树时进行剪枝，显著降低了过拟合风险，但是预剪枝基于贪心思想，本质上禁止分支展开，给决策树带来了欠拟合的风险。 

                    • 五、附件（见我的资源）

                    • 1. 习题4.3代码
                    • 2. 习题4.4代码
                    • 3. 习题4.6代码