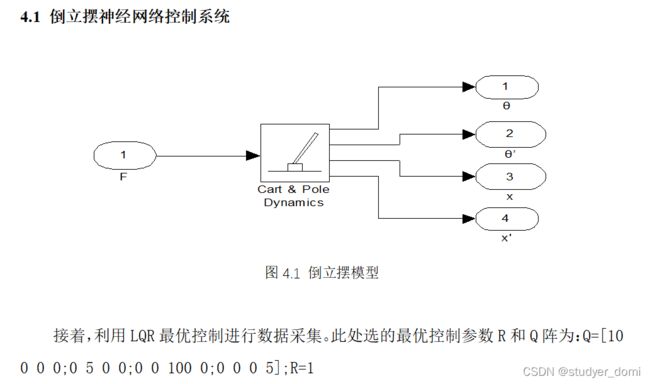
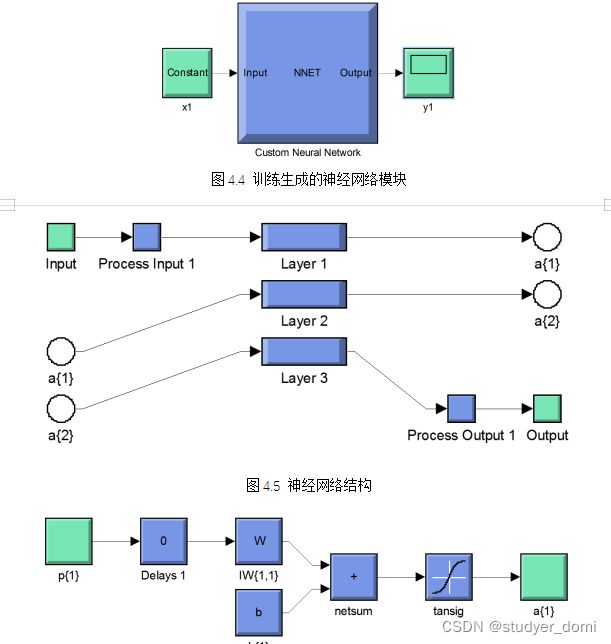
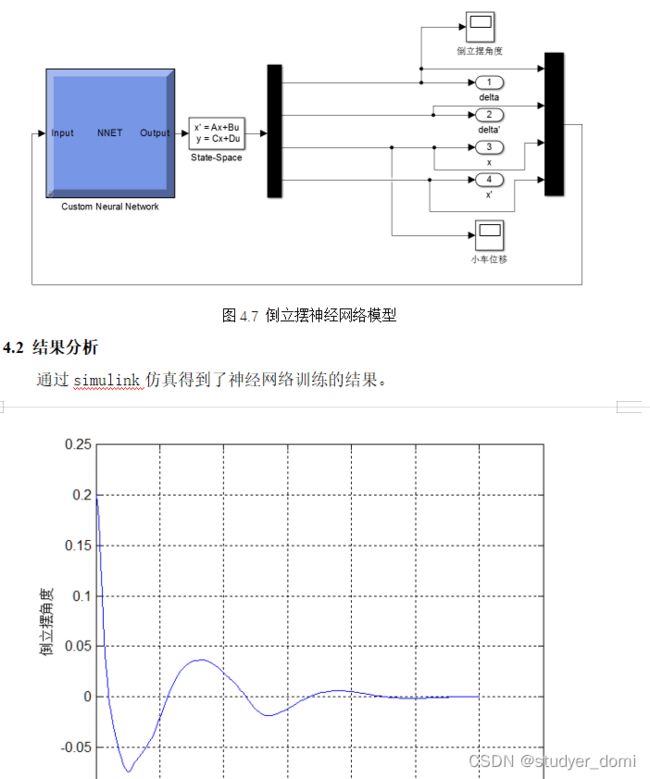
单级倒立摆的神经网络控制
倒立摆系统是一种典型的多变量、非线性、强耦合模型,它作为一种被控对象,用来检验控制理论的可行性和控制的稳定性。人工神经网络由于具有信息的分布存储、并行处理以及自学习能力等优点,在信息处理、模式识别、智能控制及系统建模等领域得到越来越广泛的应用。近年来,已有多种神经网络模型被提出并得以深入研究。神经网络从理论上可以逼近任意非线性函数,所以它特别适合控制像倒立摆这样的严重非线性、多变量系统。本文针对倒立摆,通过动力学知识,建立了倒立摆的数学模型,研究了它的传递函数和状态矩阵。通过数学软件MATLAB建立了simulink模型,分别先后提出了PID、LQR和神经网络三种控制方法,结果表明,相对于其他的2种控制方法,神经网络能够更加有效控制倒立摆。神经网络能够缩短响应时间,同时减少超调量。
关键词:倒立摆,PID, LQR,神经网络,MATLAB
倒立摆系统研究开始于20世纪50年代,早期主要集中于在直线倒立摆的建模和摆杆的平衡控制,即所谓的镇定问题。随着现代控制理论的发展,尤其是多变量线形系统理论及 最优理论的发展,70年代之后关于倒立摆系统的研究吸引了更多的关注。80年代后期,随着模糊控制的发展,用模糊控制来实现倒立摆的控制得到了大力的发展。90年代,神经网络控制开始发展,神经网络控制倒立摆以自学习为基础,用一个全新的概念进行信号处理,显示了巨大的潜力。神经网络方法用于倒立摆系统的研究更加广泛而且深入。此后的十多年以来,国内外众多学者对倒立摆系统的研究更加深入,而且取得了许多实质性额度突破,目前我国在全世界率先实现了四级倒立摆控制。
1.4.1 倒立摆系统在国外的研究现状
国外的倒立摆系统研究起步很早。在上个时代60年代,就开始对一级倒立摆系统进行研究。在60年代后期,作为一个典型的不稳定,严重非线性例证提出了倒立摆的概念,并用其检验控制方法对不稳定、非线性和快速性系统的控制能力,1966年,schacfer等人应用bang-bang控制原理实现了单级倒立摆的稳定控制,1972年sturegeon和loscutoff应用极点配置发对二级倒立摆设计了模拟控制器并使用了全纬观测器。1976年,S.Mori等设计的前馈-后馈复合控制器实现了一级倒立摆的稳定控制,并首先把倒立摆系统在平衡点附近线性化,利用状态空间的方法设计出比例微分观测器。1977年日本K.Furuta教授成功的稳定了而欸单级倒立摆,1978年K.Furuta等人采用微信处理实现了二级倒立摆控制。1980年他们有完成了二级倒立摆在倾斜轨道上的稳定控制,后来在1984年,他们应用最优状态调节器理论实现了具有双电机的三级倒立摆控制,并且采用精确线性化和近似线性化相结合的最优控制方法,实现了二级平面倒立摆的仿真与控制,1984年Wattes研究了利用 LQR(Linear Quadratic Regulator)方法控制控制倒立摆,并验证了改变性能矩阵 Q 和 R 可以得到不同的状态反馈量,从而产生不同的控制效果。从八十年代后期开始,倒立摆系统中的非线性特性得到较多的研究,并提出了一系列基于非线性分析的控制策略。1988年Charies W.Andorson在应用自学习模糊神经网络成功控制了一级摆,1992年 Furuta等人提出了倒立摆系统的变结构控制,1995 年 Fradkov 等人提出了倒立摆基于无源性的控制。另外 Wiklund 等人应用基于李亚普诺夫的方法控制了环形一级倒立摆,Yamakita等人给出了环形二级倒立摆的实验结果。1997 年日本的科研工作者们成功的实现了对平面倒立摆的控制,获得了非常好的控制效果,与此同时,瑞士国家工程研究院的 Bemhard Sprenger 等实现了直线运动机械臂的平面倒立摆的控制,并且具有很好的鲁棒性。 Christian Wachinger研究了平面中倒置的n杆摆的问题。 采用了描述形式和对应于普通微分方程组(ODE)的状态空间形式。 描述了用于解决ODE的模拟系统,并且开发了用于单杆和双杆壳的控制器。 此外,训练了用于控制倒立摆的任务的神经网络。VALERI MLADENOV研究了两个神经网络控制器将附接到推车的摆锤从初始向下位置摆动到直立位置并保持该状态。两个控制器都能够从不同的初始角度学习正在摆放的演示行为,并将直立位置的倒立摆平衡。Tim Callinan 采用人造神经网络(ANN)的领域,并将其应用于倒立摆控制问题。倒立摆通常用于对新的控制技术进行基准测量,因为它是一种高度非线性的不稳定系统。神经网络具有独特的特征,使得它们能够控制非线性系统。前馈和反复神经网络用于对倒立摆进行建模。还研究了多输出在线识别。开发了用于倒立摆的神经控制器。采用传统的控制方法来制定控制法来稳定倒立摆。训练前馈网络来模拟控制法。神经控制显示,如果系统发生干扰,神经网络就会学习抵消这种干扰。最后,实时掌握识别和控制知识倒立钻机。开发了一种在线自适应神经网络来建模实时系统。
1.4.2 倒立摆系统在国内的研究现状
国内是从 80 年代开始对倒立摆进行研究的,1982 年西安交通大学完成了二级倒立摆系统的研究和控制,采用了最优控制和降纬观测器,以模拟电路实现;1983年国防科技大学完成了一级倒立摆系统的研究和控制;1987 年上海机械学院完成了一、二级倒立摆系统的研制,并且完成了二级倒立摆在倾斜轨道上的控制。北京航空航天大学张明廉教授领导的课题组,提出了“拟人智能控制理论”框架,并于 1994 年 8 月成功地实现单电机控制的三级倒立摆。1995 年任章等应用振荡控制理论,通过在倒立摆支撑点的垂直方向上加入一个零均值的高频振荡信号,改善了倒立摆系统本身的稳定。1996 年翁正新等利用带观测器的∞H 状态反馈控制器对二级倒立摆系统进行了仿真控制。1997 年翁正新等利用同样的方法对倾斜轨道上的二级倒立摆进行了仿真控制。1998 年蒋国飞等将 Q 学习算法和BP 神经网络有效结合,实现了状态未离散化的倒立摆的无模型学习控制。2000 年刘妹琴等用进化 RBF 神经网络控制二级倒立摆。2001 年单波等利用基于神经网络的预测控制算法对倒立摆的控制进行了仿真。
我国的倒立摆研究虽然起步比较晚,但是随着用于倒立摆系统的控制理论和方法的广泛应用,国内很多大学和科研机构都对倒立摆进行了大量卓有成效的研究工作。现在,我国的倒立摆研究在某些方面已经走在了世界的前列。李德毅院士在国际上最早提出“隶属云”理论,并用该方法实现了三级倒立摆的智能控制;北京师范大学李洪兴教授的变论域模糊控制算法,也成功的应用于三级倒立摆的控制,效果极佳;2002 年 8 月,李洪兴教授应用变论域自适应模糊控制算法控制直线倒立摆,成功地实现了全球首例“四级倒立摆实物系统控制”,填补了当时的世界空白,继此之后,2003 年 4 月李洪兴教授领导的“复杂系统智能控制实验室”应用具有高维 PID 调节功能的变论域自适应控制理论实现了对平面运动二级倒立摆实物系统的控制,之后,于 2003 年 10 月在世界上第一成功实现了平面三级倒立摆实物系统的控制。由此项理论产生的方法和技术将在半导体及精密仪器加工、机器人技术、导弹拦截控制系统、航空器对接控制技术等方面具有广阔的开发利用前景。 郭维运用牛顿动力学方法对一阶倒立摆进行了数学建模, 并利用极点配置的方法设计了控制器, 最后在 M ATLAB 环境下进行了仿真研究。仿真结果表明, 该方案可以得到较为满意的结果。为了实现对绝对不稳定的非线性多变量倒立摆系统的控制, 刘文秀采用了状态反馈极点配置和 LQ R 控制 2 种方法。状态反馈极点配置是将多变量系统的闭环系统极点配置在期望的位置上, 从而使系统满足瞬态和稳态性能指标。LQ R 算法是在一定的性能指标下, 利用最少的控制能量, 来达到最小的状态误差。通过 M atlab 软件仿真实验, 发现 2 种控制方法对于倒立摆这种不稳定的系统有一定的控制作用, 证明了两种控制方案的可行性和有效性。 仿真表明二次型最优控制有较小的振荡和超调量, 对系统有更好的控制效果。肖力龙利用拉格朗日建模方法推导出直线一级倒立摆系统的数学模型,然后对其进行局部线性化,并由此推导出了系统的状态方程。接下来采用能量反馈的方法进行倒立摆的起摆控制,在平衡点附近切换并采用现代控制理论中的状态空问极点配置及线性二次型最优控制以实现稳定控制。对系统设计控制器,并进行了仿真,确定了控制器的各个参数。最后编写控制软件分别在SimulinkReal.Time Workshop与Visual C++6.0环境下实现了实时控制。仿真和实时控制结果表明该方法对单级直线倒立摆系统的起摆与稳定控制具有很好的效果。同时可以看到利用拉格朗日建模方法在实现倒立摆的稳定控制时(其数学模型中不含小车质量及小车与导轨间摩擦系数之参数)可以不依赖实际系统中某些参数的精确性。
PID控制器英文全称为Proportion-Integration-Differentiation,即比例-积分-微分控制器。 他由由比例单元 P、积分单元 I 和微分单元 D 组成。通过Kp,Ki和Kd三个参数的设定。PID控制器主要适用于基本线性和动态特性不随时间变化的系统。
PID 控制器是一个在工业控制应用中常见的反馈回路部件,这个控制器把收集到的数据和一个参考值进行比较,然后把这个差别用于计算新的输入值,这个新的输入值的目的是可以让系统的数据达到或者保持在参考值。和其他简单的控制运算不同,PID控制器可以根据历史数据和差别的出现率来调整输入值,这样可以使系统更加准确,更加稳定。可以通过数学的方法证明,在其他控制方法导致系统有稳定误差或过程反复的情况下,一个PID反馈回路却可以保持系统的稳定。
人脑是产生自然智能的源泉,是真正出色的并行计算机。人工神经网络(Artificial NeuralNetworks, 简称ANN)是在人类对其大脑神经网络认识理解的基础上人工构造的能够实现某种功能的神经网 络,它是理论化 的人脑神经网络的数学模型,是基于模仿大脑神经网络结构和功能而建立的一种非算法的信息处 理系统。
人工神经网络吸取了生物神经网络的许多优点,因而有其固有的特点:
(1)、高度并行性:人工神经网络是由许多相同的简单处理单元并联组合而成,使其对信息的处理 能力与效果惊人。
(2)、高度非线性全局作用:人工神经网络每个神经元接受大量其它神经元的输入,并通过并行网络产生输出,影响其它神经元。网络之间的这种相互制约和相互影响,实现了从输入状态到输出状态空间的非线性映射.从全局的观点来看,网络整体性能不是网络局部性能的简单迭加,而表现出某种集体性的行为。
(3)、良好的容错性与联想记忆功能:人工神经网络通过自身的网络结构能够实现对信息的记忆,而所记忆的 信息是存储在神经元之间的权值中。从单个权值中看不出所存储的信息内容,因而是分布式的存储方式,这使得网络具有良好的容错性,既能进行模式信息处理工作, 有能进行模式联想等的模式信息处理工作,又能进行模式识别工作。
(4)、十分强的自适应、自学习功能:人工神经网络可以通过训练和学习来获得网络的权值与结构,呈现出很强的自学习能力和对环境的适应能力。
3.1.1 人工神经网络发展的回顾
一般认为,最早用数学模型对神经系统中的神经元进行理论建模的是美国心理学家麦卡洛克(W.McCulloch)和数学家皮茨(W.Pitts)。他们于1943年建立了MP神经元模型。MP神经元模型首次简单的数学模型模仿出生物神经元活动功能,并揭示了通过神经元的相互连接和简单的数学计算,可以进行相当复杂的逻辑运算这一令人兴奋的事实1957年,美国计算机学家罗森布拉特(F.Rosenblatt)提出了著名的感知器(Perceptron)模型。它是一个具有连续可调权值矢量的MP神经网络模型,经过训练可达到对一定输入矢量模式进行识别的目的。1959年,当时的另外两位美国工程师威德罗(B.Widrow)和霍夫(M.Hoff)提出了自适应线性元件(Adaptive linear element,简称Adaline)。它是感知器的变化形式,尤其在权失量的算法上进行了改进,提高了训练收敛速度和精度。他们从工程实际出发,不仅在计算机上模拟了这种神经网络,而且还做成了硬件,并将训练后的人工神经网络成功地用于的小通讯中的回波和噪声,成为第一个用于解决实际问题的人工神经网络。1969年,人工智能的创始人之一明斯基(M.Minsky)和帕伯特(S.Papert)在合著的《感知器》一书中对以单层感知器为代表的简单人工神经网络的功能及局限性进行了深入分析。他们指出,单层感知器只能进行线性分类,对线性不可分的输入模式无能为力,而其解决的办法是设计出具有隐含层的多层神经网络,但是要找到一个有效修正权矢量的学习算法并不容易。这一结论使得当时许多神经网络研究者感到前途渺茫,客观上对神经网络理论的发展起了一定的消极作用。美国学者霍普菲尔德(J.Hopfield)对人工神经网络研究的复苏起到了关键性的作用。1982年,他提出了霍普菲尔的网络模型,将能量函数引入到对称反馈网络中,是网络稳定性有了明显的判据,并利用提出的网络的神经计算能力来解决条件优化问题。另外,霍普菲尔德网络模型可以用电子模拟线路来实现,从而由此还兴起了对新一代电子神经计算机的研究。另一个突破性的研究成果是儒默哈特(D.E.Rumelhart)等人在1986年提出的解决多层神经网络权值修正的算法——误差反向传播法,简称BP算法,找到了解决明斯基和帕伯特提出的问题的办法,从而给人工神经网络增添了活力。
![]()