图卷积神经网络(GCN)浅浅析

多层图卷积网络（GCN）的层间传播规则为：
$$H^{(l+1)}=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)}\right)$$
其中，$\tilde{A}=A+I_N$，$A$为图的邻接矩阵，$I_N$为单位矩阵。${\tilde{D}}_{ii}={\sum }_j{\tilde{A}}_{ij}$。$W^{(l)}$是特定层的可训练权重参数。$\sigma (\cdot )$是一个激活函数。

以下图为例来说明这些参数是如何产生的:

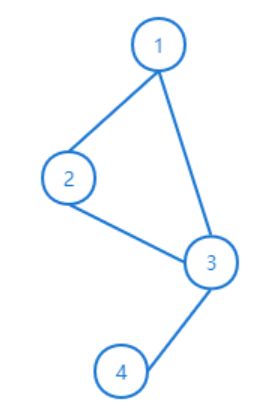
其邻接矩阵A为：

$$\begin{gathered} A: \\ [[0.1.1.0.] \\ [1.0.1.0.] \\ [1.1.0.1.] \\ [0.0.1.0.]] \end{gathered}$$

$\tilde{A}=A+I_N$为：

$$\begin{gathered} \tilde{A}: \\ [[1.1.1.0.] \\ [1.1.1.0.] \\ [1.1.1.1.] \\ [0.0.1.1.]] \end{gathered}$$

${\tilde{D}}_{ii}={\sum }_j{\tilde{A}}_{ij}$为（相当于度矩阵）：

$$\begin{gathered} \tilde{D}: \\ [[3.0.0.0.] \\ [0.3.0.0.] \\ [0.0.4.0.] \\ [0.0.0.2.]] \end{gathered}$$

${\tilde{D}}^{-\frac{1}{2}}$为：

$$\begin{gathered} {\tilde{D}}^{-\frac{1}{2}}: \\ [[0.577350270.0.0.] \\ [0.0.577350270.0.] \\ [0.0.0.50.] \\ [0.0.0.0.70710678]] \end{gathered}$$

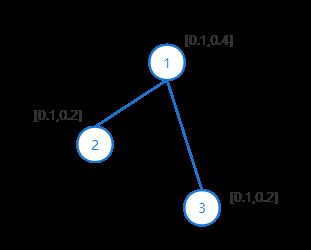
以下面一个简单的无向图说明计算代表什么含义：

计算公式为：
$$H^{(l+1)}=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)}\right)$$
先不考虑公式中的${\tilde{D}}^{-\frac{1}{2}}$，即只考虑$H^{(l+1)}=\sigma \left(\tilde{A}{H}^{(l)}{W}^{(l)}\right)$

邻接矩阵$A$和$\tilde{A}$为：
$$\begin{gathered} A= \\ [[011] \\ [100] \\ [100]] \\ \tilde{A}= \\ [[111] \\ [110] \\ [101]] \end{gathered}$$
图中每个节点的特征组成的特征向量矩阵为：
$$\begin{gathered} X= \\ [[0.10.4] \\ [0.20.3] \\ [0.10.2]] \end{gathered}$$
在只考虑邻接邻接矩阵时，即计算公式为：$H^{(l+1)}=\sigma \left(A{H}^{(l)}{W}^{(l)}\right)$。计算过程为（在未与权重相乘的情况下）：
$$\begin{gathered} [[011][[0.10.4][[0.2+0.10.3+0.2] \\ [100]\ast [0.20.3]=[0.10.4] \\ [100]][0.10.2]][0.10.4]] \end{gathered}$$
现在每一个节点的特征就变成了其所有邻居节点的特征值的和。例如第一个节点的特征值变为了[0.2+0.1 0.3+0.2]，这就i是2、3节点的和。

下面看一下在考虑邻接矩阵加上单位矩阵的情况下计算过程有什么含义，其计算公式为：$H^{(l+1)}=\sigma \left(\tilde{A}{H}^{(l)}{W}^{(l)}\right)$，计算过程为（在未与权重相乘的情况下）：
$$\begin{gathered} [[111][[0.10.4][[0.2+0.1+0.10.4+0.3+0.2] \\ [110]\ast [0.20.3]=[0.1+0.20.4+0.3] \\ [101]][0.10.2]][0.1+0.10.4+0.2]] \end{gathered}$$
在邻接矩阵加上单位矩阵之后，每个节点的特征值就变成了自身节点和所有邻居节点特征值进行求和。

如果某一个节点的邻居节点比较多，那么相加之后的特征值就变得非常的大，因此就需要对其进行归一化，而${\tilde{D}}^{-\frac{1}{2}}$的作用就起到了归一化的作用，因此GCN的层间传播规则就是$H^{(l+1)}=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)}\right)$。

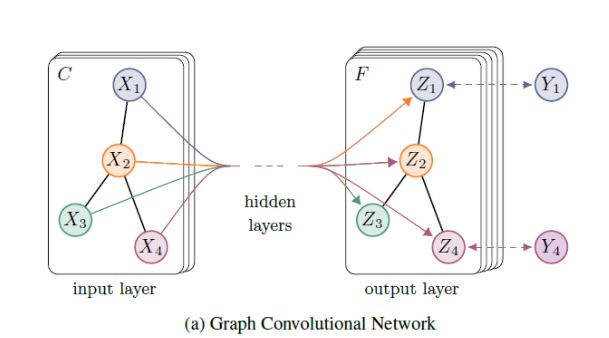
下图为GCN的一个示意图，输入一个特征维度为C的图结构，在经过GCN之后得到一个新的图，图中每一个节点的特征及其维度发生变化（由C维变为F维），但是图的结构始终不变。

最后一层GCN产生的图用于具体的任务。在分类任务中，一般对图中每一个节点进行分类，因此：

1. 最后一层GCN的隐层特征数等于类别数，直接用于softmax输出概率。
2. 在输出的F维特征后，再接一个全连接层，然后转维与类别数相同的维度。

总结一下

以具有对称邻接矩阵A的图上进行半监督的节点分类的两层GCN为例，首先在预处理步骤中计算$\hat{A}={\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$，模型的前向计算为：
$$Z=f(X,A)=\mathrm{softmax}\left(\hat{A}\mathrm{ReLU}\left(\hat{A}X{W}^{(0)}\right)W^{(1)}\right)$$
$W^{(0)}\in {\mathbb{R}}^{C\times H}$是一个具有$H$维特征的隐藏层的输入-隐藏权重矩阵。$W^{(1)}\in {\mathbb{R}}^{H\times F}$是一个隐藏到输出的权重矩阵。softmax激活函数。对于分类任务，使用交叉熵损失函数：
$$\mathcal{L}=-\sum _{l\in {\mathcal{Y}}_L}\sum _{f=1}^F{Y}_{lf}\ln Z_{lf}$$

代码部分

首先导入所使用的包。

import scipy.sparse as sp
import numpy as np
import torch
import math
from torch.nn.parameter import Parameter
import torch.nn as nn
import torch.nn.functional as F
import time
import argparse
import torch.optim as optim
from visdom import Visdom

代码地址：https://github.com/tkipf/pygcn

1、数据处理

cora数据集由机器学习论文组成。这些论文分为以下七类之一：

1. Case_Based
2. Genetic_Algorithms
3. Neural_Networks、
4. Probabilistic_Methods
5. Reinforcement_Learning
6. Rule_Learning
7. Theory

cora数据集包括两个文件：

1. cora.content文件为所有数据的信息，每行包括 节点编号 ，特征向量，所属类别。
2. cora.cites文件为边的信息，每行为节点1，节点2，代表这两个节点相连接构成一条边。

数据处理部分的主要作用为：

1. 利用边的信息生成邻接矩阵，然后对其进行归一化处理，在论文中对其进行归一化的处理方式为：$\hat{A}={\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$，而在代码实现中的归一化方式为：$\hat{A}={\tilde{D}}^{-1}\tilde{A}$。
2. 处理特征向量，并对特征向量进行归一化（论文中没有归一化，可有可无）。
3. 划分训练集、验证集和测试集。

具体代码如下。

def encode_onehot(labels):
    """
    将标签转为one_hot编码
    :param labels:
    :return:
    """
    #获取标签中所有的类别
    #set 创建一个无序不重复的集合
    classes = set(labels)
    #为每一个标签分配一个one-hot编码
    #identity函数用于一个n*n的单位矩阵(主对角线元素全为1，其余全为0的矩阵)。
    classes_dict = {c : np.identity(len(classes))[i,:] for i,c in enumerate(classes)}
    #将原来的标签转为one-hot编码
    labels_onehot = np.array(list(map(classes_dict.get,labels)),dtype = np.int32)
    return labels_onehot

def normalize(mx):
    '''
    行归一化稀疏矩阵
    :param mx:
    :return:
    '''
    #矩阵行求和
    rowsum = np.array(mx.sum(1))
    #求和的-1次方
    r_inv = np.power(rowsum,-1).flatten()
    #如果是inf，转换成0
    r_inv[np.isinf(r_inv)] = 0.
    #构造对角矩阵
    r_mat_inv = sp.diags(r_inv)
    #构造D^(-1)*A ， 归一化操作
    #在公式中是D^(-1/2)*A*D^(-1/2),这里是一个简化后的归一化操作
    mx = r_mat_inv.dot(mx)
    return mx


def sparse_mx_to_torch_sparse_tensor(sparse_mx):
    '''
    将一个庞大的稀疏矩阵转换为torch稀疏张量。
    :param sparse_mx:
    :return:
    '''
    sparse_mx = sparse_mx.tocoo().astype(np.float32)
    indices = torch.from_numpy(
        np.vstack((sparse_mx.row,sparse_mx.col)).astype(np.int64))
    values = torch.from_numpy(sparse_mx.data)
    shape = torch.Size(sparse_mx.shape)
    return torch.sparse.FloatTensor(indices,values,shape)



def load_data(path = "./data/cora/", dataset = "cora"):
    print('Loading {} dataset...'.format(dataset))

    #从文本文件加载数据
    #genfromtxt():从文本文件加载数据，同时处理数据。
    #idx_features_labels的形状：(节点数，编号+特征+类别) = (2708,1435)
    idx_features_labels = np.genfromtxt("{}{}.content".format(path,dataset),dtype = np.dtype(str))

    #取每一个节点的特征值，同时转为稀疏矩阵 .A可以取其值
    features = sp.csr_matrix(idx_features_labels[:,1:-1],dtype = np.float32)
    #将标签值转为one-hot
    labels = encode_onehot(idx_features_labels[:,-1])

    #获取每个节点的id
    idx = np.array(idx_features_labels[:,0],dtype = np.int32)
    #将所有的id按照顺序 构建一个 字典 key为源数据的节点顺序，value为从0到1的顺序值
    idx_map = {j:i for i,j in enumerate(idx)}
    #读取边信息，每行数据由两个节点，代表这两个节点相连接构成一条边
    edges_unordered = np.genfromtxt("{}{}.cites".format(path,dataset),dtype = np.int32)
    #对每个节点 重新编号
    #flatten() :对多维数据进行降维
    edges = np.array(list(map(idx_map.get,edges_unordered.flatten())),dtype = np.int32).reshape(edges_unordered.shape)
    #构建邻接矩阵
    #coo_matrix：生成坐标格式的矩阵
    adj = sp.coo_matrix((np.ones(edges.shape[0]),(edges[:,0],edges[:,1])),
                        shape = (labels.shape[0],labels.shape[0]),
                        dtype = np.float32)
    #计算转置矩阵
    adj = adj + adj.T.multiply(adj.T > adj) - adj.multiply(adj.T > adj)

    #对特征进行归一化，不是完全必要的
    features = normalize(features)
    #对A+I进行归一化，
    adj = normalize(adj + sp.eye(adj.shape[0]))

    #划分训练、验证、测试的样本
    idx_train = range(140)
    idx_val = range(200,500)
    idx_test = range(500,1500)

    #将numpy数据转为torch格式
    features = torch.FloatTensor(np.array(features.todense()))
    labels = torch.LongTensor(np.where(labels)[1])
    adj = sparse_mx_to_torch_sparse_tensor(adj)

    idx_train = torch.LongTensor(idx_train)
    idx_val = torch.LongTensor(idx_val)
    idx_test = torch.LongTensor(idx_test)

    return adj,features,labels,idx_train,idx_val,idx_test

2、GCN的计算过程

计算过程就是使用经过处理后的邻接矩阵与权重和特征向量进行运算，其运算公式为：$\left(\hat{A} X W\right) $。具体代码如下：

class GraphConvolution(nn.Module):
    """
    Simple GCN layer, similar to https://arxiv.org/abs/1609.02907
    """
    def __init__(self,in_features,out_features,bias = True):
        super(GraphConvolution, self).__init__()
        #输入特征维度
        self.in_features = in_features
        #输出特征维度
        self.out_features = out_features
        #权重参数
        self.weight = Parameter(torch.FloatTensor(in_features,out_features))
        #偏置
        if bias:
            self.bias = Parameter(torch.FloatTensor(out_features))
        else:
            self.register_parameter('bias',None)
        self.reset_parameters()
    #初始化参数
    def reset_parameters(self):
        stdv = 1. / math.sqrt(self.weight.size(1))
        self.weight.data.uniform_(-stdv,stdv)
        if self.bias is not None:
            self.bias.data.uniform_(-stdv,stdv)


    def forward(self,input,adj):
        #特征向量与权重相乘
        support = torch.mm(input,self.weight)
        #然后再与处理后的邻接矩阵相乘
        output = torch.spmm(adj,support)
        #是否加上偏置
        if self.bias is not None:
            return output + self.bias
        else:
            return output
    #用于显示属性
    def __repr__(self):
        return self.__class__.__name__ + ' ('\
            + str(self.in_features) + ' -> '\
            + str(self.out_features) + ')'

3、构建一个两层的GCN网络

使用上面的GCN的计算过程就可以搭建一个两层的GCN网络，其中还使用了dropout，其公式为：$\mathrm{softmax}\left(\hat{A}\mathrm{ReLU}\left(\hat{A}X{W}^{(0)}\right)W^{(1)}\right)$。代码如下：

class GCN(nn.Module):
    def __init__(self,nfeat,nhid,nclass,dropout):
        super(GCN, self).__init__()
        self.gc1 = GraphConvolution(nfeat,nhid)
        self.gc2 = GraphConvolution(nhid,nclass)
        self.dropout = dropout

    def forward(self,x,adj):
        x = F.relu(self.gc1(x,adj))
        x = F.dropout(x,self.dropout,training = self.training)
        x = self.gc2(x,adj)
        return F.log_softmax(x,dim = 1)

4、模型训练

定义一个计算准确度的函数。

def accuracy(output,labels):
    preds = output.max(1)[1].type_as(labels)
    correct = preds.eq(labels).double()
    correct = correct.sum()
    return correct / len(labels)

下面为训练模型的代码

#设置训练的参数
parser = argparse.ArgumentParser()
parser.add_argument('--no-cuda', action='store_true', default=False,
                    help='Disables CUDA training.')
parser.add_argument('--fastmode', action='store_true', default=False,
                    help='Validate during training pass.')
parser.add_argument('--seed', type=int, default=42, help='Random seed.')
parser.add_argument('--epochs', type=int, default=200,
                    help='Number of epochs to train.')
parser.add_argument('--lr', type=float, default=0.01,
                    help='Initial learning rate.')
parser.add_argument('--weight_decay', type=float, default=5e-4,
                    help='Weight decay (L2 loss on parameters).')
parser.add_argument('--hidden', type=int, default=16,
                    help='Number of hidden units.')
parser.add_argument('--dropout', type=float, default=0.5,
                    help='Dropout rate (1 - keep probability).')

#args = parser.parse_args()
args = parser.parse_known_args()[0]
args.cuda = not args.no_cuda and torch.cuda.is_available()

#设置随机种子
np.random.seed(args.seed)
torch.manual_seed(args.seed)
if args.cuda:
    torch.cuda.manual_seed(args.seed)

#加载数据
adj,features,labels,idx_train,idx_val,idx_test = load_data()

#加载模型和优化器
model = GCN(nfeat = features.shape[1],
            nhid = args.hidden,
            nclass = labels.max().item() + 1,
            dropout = args.dropout)
optimizer = optim.Adam(model.parameters(),
                       lr = args.lr,weight_decay = args.weight_decay)

#如果使用GPU，将数据传入GPU
if model.cuda():
    model.cuda()
    features = features.cuda()
    adj = adj.cuda()
    labels = labels.cuda()
    idx_train = idx_train.cuda()
    idx_val = idx_val.cuda()
    idx_test = idx_test.cuda()

#训练函数
def train(epoch,viz):
    t = time.time()
    model.train()
    optimizer.zero_grad()
    output = model(features,adj)
    #计算训练损失和正确率
    loss_train = F.nll_loss(output[idx_train],labels[idx_train])
    acc_train = accuracy(output[idx_train],labels[idx_train])
    loss_train.backward()
    optimizer.step()

    if not args.fastmode:
        model.eval()
        output = model(features,adj)

    #计算验证损失和正确率
    loss_val = F.nll_loss(output[idx_val],labels[idx_val])
    acc_val = accuracy(output[idx_val],labels[idx_val])
    viz.line(Y=np.column_stack((acc_train.cpu(),acc_val.cpu())),
             X=np.column_stack((epoch, epoch)),
                    win='line1',
                    opts=dict(legend=['acc_train','acc_val'],
                        title='acc',
                        xlabel='epoch',
                        ylabel='acc'),
                    update = None if epoch == 0 else 'append'
                    )
    viz.line(Y=np.column_stack((loss_train.detach().cpu().numpy(),loss_val.detach().cpu().numpy())),
             X=np.column_stack((epoch, epoch)),
                    win='line2',
                    opts=dict(legend=['loss_train','loss_val'],
                        title='loss',
                        xlabel='epoch',
                        ylabel='loss'),
                    update = None if epoch == 0 else 'append'
                    )
	'''
    print('Epoch: {:04d}'.format(epoch + 1),
          'loss_train: {:.4f}'.format(loss_train.item()),
          'acc_train: {:.4f}'.format(acc_train.item()),
          'loss_val: {:.4f}'.format(loss_val.item()),
          'acc_val: {:.4f}'.format(acc_val.item()),
          'time: {:.4f}s'.format(time.time()  - t))
    '''
             
#测试函数
def test():
    model.eval()
    output = model(features,adj)
    loss_test = F.nll_loss(output[idx_test],labels[idx_test])
    acc_test = accuracy(output[idx_test],labels[idx_test])
    print("Test set results:",
          "loss= {:.4f}".format(loss_test.item()),
          "accuracy= {:.4f}".format(acc_test.item()))

开始训练

t_total = time.time()
viz = Visdom(env='test1')
for epoch in range(args.epochs):
    train(epoch,viz)
print('Optimization Finished!')
print("Total time elapsed: {:.4f}s".format(time.time() - t_total))

# Testing
test()

Optimization Finished!
Total time elapsed: 8.1138s
Test set results: loss= 0.7548 accuracy= 0.8260

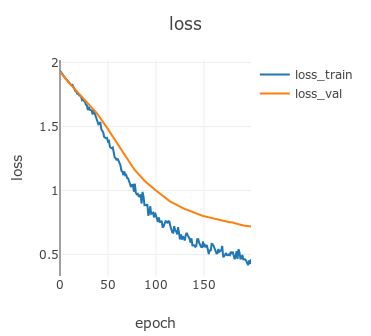
训练过程中损失可视化曲线为：

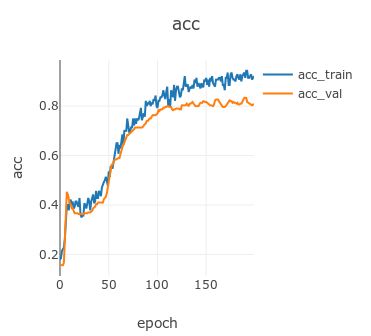
训练过程中准确率可视化曲线为：