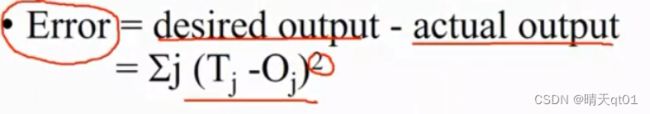【自然语言处理与文本分析】非结构文本转结构数据。BP神经网络,反向传播神经网络,神经网络优化的底层原理,梯度优化法
-
-
- BP(Back Propagation(BP)) Neuel Networks
-
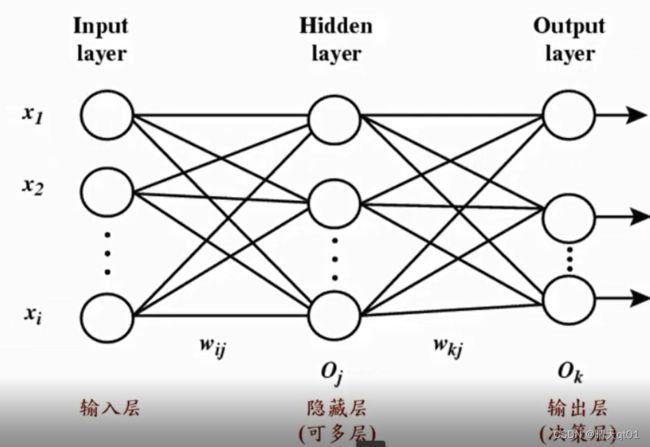
反向传播神经网络:多层感知机
输入层的神经元(接受外来数据)
异常层的神经元(用于增加处理问题的能力)
还有输出层的神经元(做决策)
神经键,就是权重值。用于连接神经元
隐藏层可以变多,层数越多,节点越多,说明处理问题的能力越多。
之后深度学习会说明,隐藏层数是越多越好,还是节点越多越好。
比如现在有10个数,我们要选择2个层,5个神经元,还是一个层10个神经元呢?
其实通过研究,还是选择多个层次,比较好,深度学习就是对多层次的研究
以往的BP神经网络,隐藏层一般都比较少只有一层,因为如果隐藏层数多,要求的数据也要多,否则就会出现过拟合的现象。
所以我们的神经网络一般都限制在1-2层(神经网络就没有这种情况)
也可以没有隐藏层
案例:
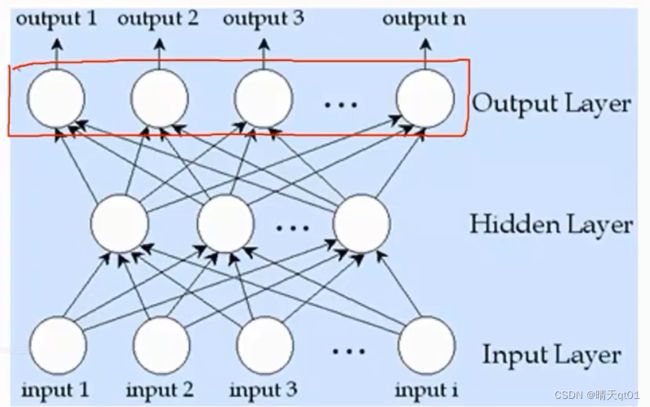
输出层只有一个神经元,说明它要做的问题,是二分类的问题,或者做的是回归的问题。输出层就只有一个。那么它可以处理的就都是比较简单,而且做二分类的神经网络。
如果输出节点是多分类的问题,有隐藏层,那么我们就可以做多分类的复杂节点,否则没有隐藏层,就只能做单分类问题。
案例:
输出层是5种不同杂志偏好的概率。
特别说明:以我们这个案例里面,他的输出层概率总和不一定要为1,因为一个人可以对多个杂志有偏好,我们就不用使用soft max函数处理。
遇到不同的问题。我们要用理解原理,才能知道怎么进行修改,确保结果正确。
我们这里一共有4个字段,作为输入字段。
神经网络只能接受数值型的输入,遇见类别型字段,神经网络的处理方法,一般会把它摊平,比如年龄有3个程度。我们就要用3个神经元对它进行处理。
只能接受数值输入。输入的数字,我们会希望它介于0-1之间。输出结果我们也会希望在0-1之间。
分类,有没有房子,有没有车子,各用一个节点。有输入1,无输入没有。区域也是一样。所以这次神经网络,我们有4个字段,使用了9个输入层神经元。
隐藏层和输入层,是完全连接。但是跨层不连接(BP神经网络特有的 fully connected),然后由左往右连接,不能回头。权重值,是由右往左来进行修改(back ground)。等会有案例。
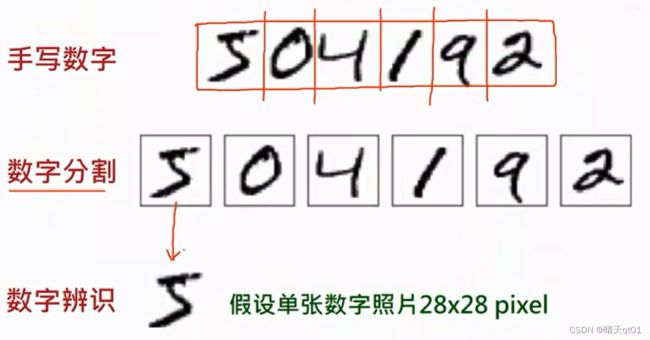
手写数字的识别案例:
神经网络的输入必须是固定值,所以像素的大小也得固定。
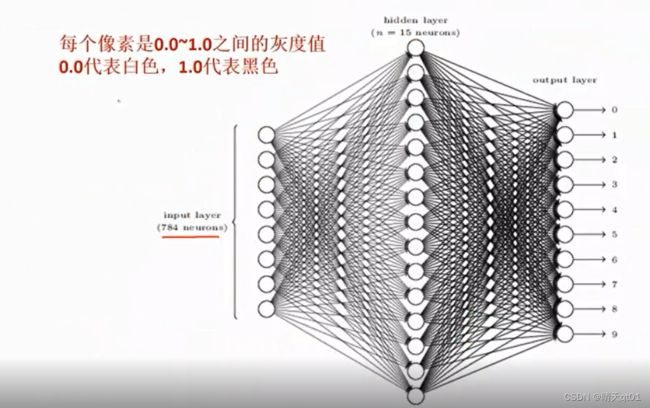
,它将每个点,当做一个神经元,白色代表最亮:可能就输入255,黑色代表最暗,代表0
这里面我们用0代表白色,1代表黑色。
0~1之间的灰度值。
所以我们做图形辨识的时候,我们一般都会把数值除以255,尽量让输入的数值为0~1之间,1为白色,0为白色。因为我们普遍认为0代表白色,所以也可以用1减去这个值。
输出0-9的概率值。因为这里只能选择一个数。所以我们可以用softmax对结果字段进行处理。
隐藏层越多,处理复杂问题的能力就越强。
但是如果你设置的太多,就会导致神经网络过拟合的问题,所以我们要拿捏好隐藏层的数量,数量比较少的隐藏层,才能体现它的学习能力。比较少的隐藏层和比较多的隐藏层结果相同的时候,我建议使用较少的隐藏层,因为,较多的隐藏层实际会导致它不是神经网络,更多的是去记忆点的位置。只有少的隐藏层,它才会真正去学习。
问题越复杂是怎么定义呢,
隐藏层最大数量=输入层的节点个数乘以输出层的节点个数开根号,
然后向下调整。比如我们这里输入层是9,输出层是5,结果就大约是6
我们就对6进行向下调整,看结果如何,比如隐藏层数量从6到4结果都是差不多不变,但是从4到3结果突然变差,那么就说明智能不足了,4个差不多。 这个要不断尝试,看它的泛化能力。
总结Bp神经网络的步骤:
1.建立网络架构:
输入层的表示方法(数值型,类别型,尽量0-1)
选择输入层的层数,隐藏层的节点个数。输入层的节点个数
2.选择训练数据
得到一组的权重值,让我们得到的输出向量与目标向量的误差最小
3.训练结果:
训练好的案例:
所以我们就说这个人,可能对汽车杂志,搞笑杂志感兴趣,结果因为不大于1,所以我们就将它视为概率。
但是如果这个时候训练结果并不好,那么我们就要back ground从右向左的对权重进行优化。
我们从原理上看,其实输入层和隐藏层直接的关联一般都是直接相连,不会进行处理,而隐藏层和输出层,的关联是具有构造的,构造唯一
复习一下构造内容
就是神经元的数值乘以它的权重,然后加上bias的值,然后通过激活函数(activation function)得到函数
激活函数也可以被叫做TransferFinction转变函数。
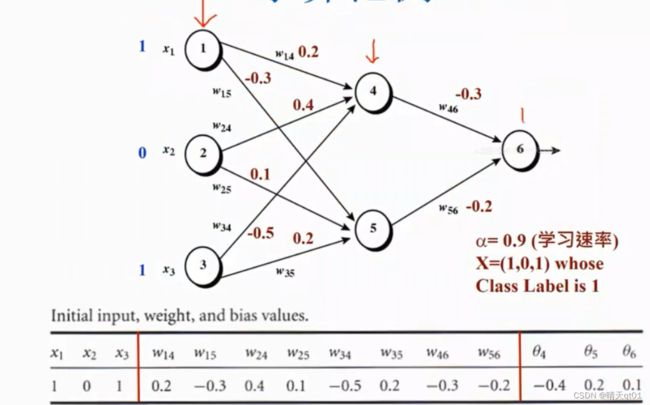
BP神经网络案例:
这是一个bp神经网络,里面有3个层次,输入层,输出层,隐藏层。而且是全线连接。
权重值随机产生。
Bias也就是里面的西塔 也是随机产生:在-1到1之间随机产生
手算介绍:
我们随机出权重,然后按路线计算隐藏层数值和输出结果,如上表。
得到0.474的结果,但是我们的目标结果是1,所以不是很理想,为什么不是很理想呢?因为我们都随机产生的权重和bias,这是从左往右逐步计算的结果。
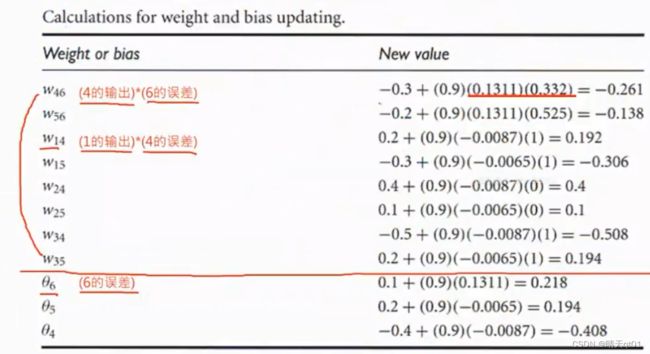
逆向权重和偏执项的修正:
那么我们现在就bakeward training逆向权重和偏执项的修正。
它会去修复隐藏层到输出层的组合函数,和激活函数。
这个修正好之后,然后再去修正输入层与隐藏层的内容。
我们在逐步从右向左修正误差的过程中,后面的误差是会影响到前面的。反向传递。
误差如何计算呢。
我们要将这个误差进行一个偏微分,就会出现极值,就可以进行修正。
这边直接给出微分结果。这些是偏微分的结果。
一般同一层的误差公式都是类似的。
这样我们就可以得到我们各项的误差(这些误差的通过)
然后我们也可以对权重的修改也得到公式建议调整的结果。一直进行跑逆向权重和偏执项的修正就可以收敛到比较好的结果。
这个修正不是一步到位的,可能进行500次,结果可能输出的就变成0.93
所以去跑神经网络是很耗费时间的。
为什么要怎么做呢,这个是为了一种情况,比如我现在的权重值是0.3,最佳值是0.25,但是你修改幅度设置很大。0.1,那么修改之后系统认为需要前进0.1,权重就变成了0.2,第二次修改又会变为0.3.来回反复,一直达不到最优。Leaning rate设置太大就会出现这种情况。所以如果学习效率设置的高,可能逼近的速度快,但是不能得到比较好的最佳值,如果比较少,可能会得到比较好的最佳值,但是它会花比较多的时间。
传统的神经网络都是我们主动设置leaning rate 。
但是在深度学习里面,就会使用动态的leaning rate 刚开始大,后面可能就小了
为什么我们需要调整多次呢,因为我们的逆向权重和偏执项的修正是通过一次微分求斜率,斜率的正负决定了权重要增加还是降低,这种方法被叫做梯度下降法,但是有时候实际的误差函数是有两个谷底的,所以我们就把BP神经网络求出的最佳值,叫做区域最佳值。