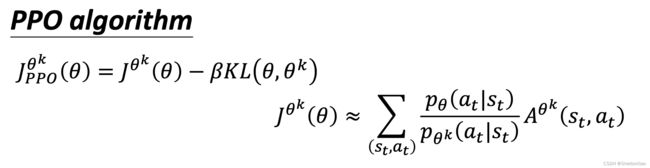【datawhale202207】强化学习:策略梯度和近端策略优化
结论速递
本篇小结了使用神经网络进行强化学习时的实现形式。为easy-rl蘑菇书的读书笔记。
神经网络此时实际上是解决输入为状态,输出为动作的多分类问题。初始化网络后,一个回合将获得多个状态-动作对,作为训练数据,蒙特卡洛法将在每个回合完成后更新网络。策略梯度是使用神经网络作为决策智能体时的优化学习目标,由多分类的交叉熵和单状态-动作对的奖励组合而成。这里的优化指的是梯度上升。
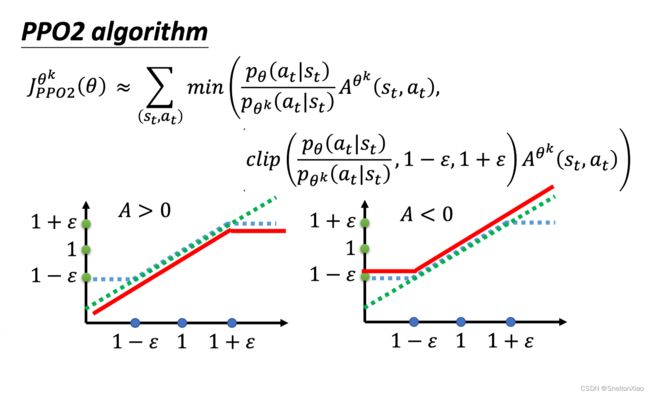
为了实现更大胆的探索,可以将探索智能体和决策智能体分开,实现异策略。此时需要注意重要性采样的问题,需要使探索智能体的动作与决策智能体尽可能接近。近端策略优化使用KL散度来完成这一限制。近端策略优化裁剪进一步把KL散度简化为裁剪(截断)函数来简化计算。
前情回顾
- 强化学习基础
目录
-
- 结论速递
- 前情回顾
- 1 策略梯度
-
- 1.1 策略梯度算法
-
- 1.1.1 强化学习与神经网络的对应
- 1.1.2 策略梯度
- 1.2 策略梯度技巧
-
- 1.2.1 添加基线
- 1.2.2 分配合适的分数
- 1.3 REINFORCE:蒙特卡洛策略梯度(基础实现)
-
- 1.3.1 蒙特卡洛策略梯度
- 1.3.2 蒙特卡洛vs时序差分方法
- 2 近端策略优化
-
- 2.1 同策略和异策略
-
- 2.1.1 异策略的具体意义
- 2.1.2 重要性采样
- 2.2 近端策略优化
-
- 2.2.1 策略限制
- 2.2.2 分类
- 参考阅读
1 策略梯度
1.1 策略梯度算法
1.1.1 强化学习与神经网络的对应
对策略(即智能体)是一个网络的情形,具体描述了强化学习各部分对应网络的部分。
对网络,本质上是针对环境反馈采取动作的多分类问题(状态-》动作):
- 输入:状态。环境反馈,可能是游戏场景图片,或是其他
- 输出:动作。动作的多分类概率
训练网络时:
- 数据:一个游戏完成,可以称为一个回合,形成一串序列数据,包含多个状态-动作对;同时可以得到总奖励(回报)R。
- 目标函数:策略梯度
- 训练方法:梯度上升更新神经元权重
1.1.2 策略梯度
每个游戏回合结束后,对应的轨迹 τ \tau τ,得到的回报为 R R R,则多次执行游戏可以得到期望:
R ˉ θ = ∑ τ R ( τ ) p θ ( τ ) \bar{R}_{\theta}=\sum_{\tau} R(\tau) p_{\theta}(\tau) Rˉθ=τ∑R(τ)pθ(τ)
假设 θ \theta θ 是一个很强的模型(对应模型里的参数),这个模型需要满足:
- 如果有一个回合 θ \theta θ 很快就死掉了,因为这种情况很少会发生,所以该回合对应的轨迹 τ \tau τ 的概率就很小;
- 如果有一个回合 θ \theta θ 都一直没有死,因为这种情况很可能发生,所以该回合对应的轨迹 τ \tau τ 的概率就很大。
神经网络正向传播的时候,是根据 θ \theta θ 算出某一个轨迹 τ \tau τ 出现的概率,接下来计算这个 τ \tau τ 的总奖励是多少。
总奖励使用这个 τ \tau τ 出现的概率进行加权,对所有的 τ \tau τ 进行求和,就是期望值。也可写成从 p θ ( τ ) p_{\theta}(\tau) pθ(τ) 这个分布采样一个轨迹 τ \tau τ,然后计算 R ( τ ) R(\tau) R(τ) 的期望值。
R ˉ θ = ∑ τ R ( τ ) p θ ( τ ) = E τ ∼ p θ ( τ ) [ R ( τ ) ] \bar{R}_{\theta}=\sum_{\tau} R(\tau) p_{\theta}(\tau)=E_{\tau \sim p_{\theta}(\tau)}[R(\tau)] Rˉθ=τ∑R(τ)pθ(τ)=Eτ∼pθ(τ)[R(τ)]
策略梯度由下式推导得到
∇ R ˉ θ = ∑ τ R ( τ ) ∇ p θ ( τ ) = ∑ τ R ( τ ) p θ ( τ ) ∇ p θ ( τ ) p θ ( τ ) = ∑ τ R ( τ ) p θ ( τ ) ∇ log p θ ( τ ) = E τ ∼ p θ ( τ ) [ R ( τ ) ∇ log p θ ( τ ) ] ≈ 1 N ∑ n = 1 N R ( τ n ) ∇ log p θ ( τ n ) = 1 N ∑ n = 1 N ∑ t = 1 T n R ( τ n ) ∇ log p θ ( a t n ∣ s t n ) \begin{aligned} \nabla \bar{R}_{\theta}&=\sum_{\tau} R(\tau) \nabla p_{\theta}(\tau)\\&=\sum_{\tau} R(\tau) p_{\theta}(\tau) \frac{\nabla p_{\theta}(\tau)}{p_{\theta}(\tau)} \\&= \sum_{\tau} R(\tau) p_{\theta}(\tau) \nabla \log p_{\theta}(\tau) \\ &=E_{\tau \sim p_{\theta}(\tau)}\left[R(\tau) \nabla \log p_{\theta}(\tau)\right]\\ &\approx \frac{1}{N} \sum_{n=1}^{N} R\left(\tau^{n}\right) \nabla \log p_{\theta}\left(\tau^{n}\right) \\ &=\frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}} R\left(\tau^{n}\right) \nabla \log p_{\theta}\left(a_{t}^{n} \mid s_{t}^{n}\right) \end{aligned} ∇Rˉθ=τ∑R(τ)∇pθ(τ)=τ∑R(τ)pθ(τ)pθ(τ)∇pθ(τ)=τ∑R(τ)pθ(τ)∇logpθ(τ)=Eτ∼pθ(τ)[R(τ)∇logpθ(τ)]≈N1n=1∑NR(τn)∇logpθ(τn)=N1n=1∑Nt=1∑TnR(τn)∇logpθ(atn∣stn)
则整个回合结束后得到的总奖励就是
1 N ∑ n = 1 N ∑ t = 1 T n R ( τ n ) log p θ ( a t n ∣ s t n ) \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}} R\left(\tau^{n}\right) \log p_{\theta}\left(a_{t}^{n} \mid s_{t}^{n}\right) N1n=1∑Nt=1∑TnR(τn)logpθ(atn∣stn)
1.2 策略梯度技巧
1.2.1 添加基线
由于探索环境的过程是采样的过程,对环境采样不充分可能导致观测数据偏态。
让奖励在0周围有益于充分采样。如下图,拉大每个分类的距离(把右变成左)
此时奖励函数为
∇ R ˉ θ ≈ 1 N ∑ n = 1 N ∑ t = 1 T n ( R ( τ n ) − b ) ∇ log p θ ( a t n ∣ s t n ) \nabla \bar{R}_{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}}\left(R\left(\tau^{n}\right)-b\right) \nabla \log p_{\theta}\left(a_{t}^{n} \mid s_{t}^{n}\right) ∇Rˉθ≈N1n=1∑Nt=1∑Tn(R(τn)−b)∇logpθ(atn∣stn)
对R(t)取期望作为基线,会是比较好的:
b ≈ E [ R ( τ ) ] b \approx E[R(\tau)] b≈E[R(τ)]
1.2.2 分配合适的分数
若对一个回合全程的所有状态-动作对采用整体的得到的奖励,会丢失中间过程的奖励信息。因此需要把中间状态-动作对的奖励单独定义出来。
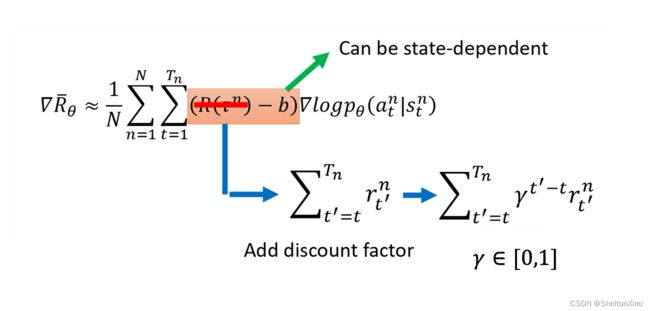
上式中把未来的奖励做一个折扣(discount),由此得到的回报被称为 Discounted Return(折扣回报)。
本质上其实是描述马尔可夫决策过程的中间状态点奖励,因此方程非常类似。
1.3 REINFORCE:蒙特卡洛策略梯度(基础实现)
1.3.1 蒙特卡洛策略梯度
这是最基础的训练方式了,即一个回合结束后进行一次训练,做一次更新。可以类比对每一条马尔科夫链(一个回合)进行一次奖励函数的更新。
具体实现上:
- 对每个状态动作对的目标函数(策略梯度):神经网络的输出和动作one-hot编码求交叉熵,再乘以奖励函数
- 对每个状态动作对的奖励函数:回合已完成,可以对每个状态计算奖励函数
未来总收益是这样计算的:
G t = ∑ k = t + 1 T γ k − t − 1 r k = r t + 1 + γ G t + 1 \begin{aligned} G_{t} &=\sum_{k=t+1}^{T} \gamma^{k-t-1} r_{k} \\ &=r_{t+1}+\gamma G_{t+1} \end{aligned} Gt=k=t+1∑Tγk−t−1rk=rt+1+γGt+1
1.3.2 蒙特卡洛vs时序差分方法
相比蒙特卡洛还是一个回合更新一次这样子的方式,时序差分 就是每个步骤都更新一下。每走一步,我就更新下,这样的更新频率会更高一点。它拿的是 Q-function 来去近似地表示我的未来总收益 G t G_t Gt。

2 近端策略优化
2.1 同策略和异策略
2.1.1 异策略的具体意义
- 如果要学习的 agent 跟和环境互动的 agent 是同一个的话, 这个叫做
on-policy(同策略)。 - 如果要学习的 agent 跟和环境互动的 agent 不是同一个的话, 那这个叫做
off-policy(异策略)。
如果我们采用异策略
用另外一个 policy, 另外一个 actor θ ′ \theta' θ′ 去跟环境做互动( θ ′ \theta' θ′ 被固定了)。用 θ ′ \theta' θ′ 收集到的数据去训练 θ \theta θ。假设我们可以用 θ ′ \theta' θ′ 收集到的数据去训练 θ \theta θ,意味着说我们可以把 θ ′ \theta' θ′ 收集到的数据用非常多次,我们可以执行梯度上升(gradient ascent)好几次,我们可以更新参数好几次, 都只要用同一笔数据就好了。因为假设 θ \theta θ 有能力学习另外一个 actor θ ′ \theta' θ′ 所采样出来的数据的话, 那 θ ′ \theta' θ′ 就只要采样一次,也许采样多一点的数据, 让 θ \theta θ 去更新很多次,这样就会比较有效率。
2.1.2 重要性采样
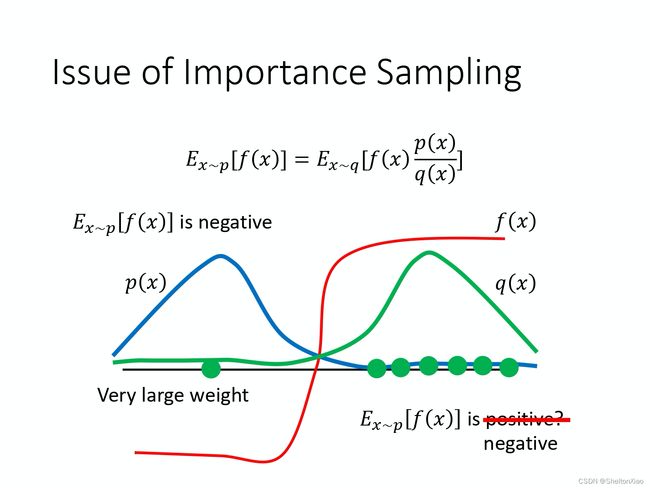
重要性采样的定义是使用另外一种分布q来逼近所求的分布p。
重要性采样
对于ー个随机变量,通常用概率密度函数来刻画该变量的概率分布特性。具体来说,给定随机变量的一个取值,可以根据概率密度函数来计算该值对应的概率(密度)。反过来,也可以根据概率密度函数提供的概率分布信息来生成随机变量的一个取值,这就是采样。因此,从某种意义上来说,采样是概率密度函数的逆向应用。与根据概率密度函数计算样本点对应的概率值不同,采样过程往往没有那么直接,通常需要根据待采样分布的具体特点来选择合适的采样策略。
假设有一个函数 f ( x ) f(x) f(x),要计算从 p 这个分布采样 x x x,再把 x x x 带到 f f f 里面,得到 f ( x ) f(x) f(x)。现在假设从q 去采样 x x x,尝试计算 f ( x ) f(x) f(x) 的期望值?
假设你的 x x x 都是从 p 采样出来的
E x ∼ p [ f ( x ) ] ≈ 1 N ∑ i = 1 N f ( x i ) E_{x \sim p}[f(x)] \approx \frac{1}{N} \sum_{i=1}^N f(x^i) Ex∼p[f(x)]≈N1i=1∑Nf(xi)
从q采样需要做一个修正。期望值 E x ∼ p [ f ( x ) ] E_{x \sim p}[f(x)] Ex∼p[f(x)] 其实就是 ∫ f ( x ) p ( x ) d x \int f(x) p(x) dx ∫f(x)p(x)dx,我们对其做如下的变换:
∫ f ( x ) p ( x ) d x = ∫ f ( x ) p ( x ) q ( x ) q ( x ) d x = E x ∼ q [ f ( x ) p ( x ) q ( x ) ] \int f(x) p(x) d x=\int f(x) \frac{p(x)}{q(x)} q(x) d x=E_{x \sim q}[f(x){\frac{p(x)}{q(x)}}] ∫f(x)p(x)dx=∫f(x)q(x)p(x)q(x)dx=Ex∼q[f(x)q(x)p(x)]
即
E x ∼ p [ f ( x ) ] = E x ∼ q [ f ( x ) p ( x ) q ( x ) ] E_{x \sim p}[f(x)]=E_{x \sim q}\left[f(x) \frac{p(x)}{q(x)}\right] Ex∼p[f(x)]=Ex∼q[f(x)q(x)p(x)]
也就是说从 q 里采样出来的每一笔数据,需要乘上一个重要性权重(importance weight) p ( x ) q ( x ) \frac{p(x)}{q(x)} q(x)p(x) 来修正这两个分布的差异。 q ( x ) q(x) q(x) 可以是任何分布,唯一的限制情况就是 q ( x ) q(x) q(x) 的概率是 0 的时候, p ( x ) p(x) p(x) 的概率不为 0,这样会没有定义。
重要性采样有一些问题。虽然理论上你可以把 p 换成任何的 q。但是在实现上,p 和 q 不能差太多。因为即使期望相同,方差也是有差距的。即采样不足时,若p和q差距很大,则目标函数方差很大,不利于学习**。
因此,需要让p和q尽可能接近。
2.2 近端策略优化
2.2.1 策略限制
利用KL散度衡量两个智能体在同一状态下行为(即输出动作)的差距,从而限制智能体的探索空间。
具体来说,在每个状态下,探索智能体的神经网络参数会更新很多次,以尽可能多的探索环境。但输出始终受到KL散度的限制。
2.2.2 分类
分为两类
参考阅读
1.强化学习蘑菇书