【机器学习算法】决策树-4 CART算法和CHAID算法
目录
CART分类树算法
CART字段选择依据
CART分类树的剪枝作法
CART处理连续型变量:
CHAID分类树算法
-CHAID的字段选择方式
剪枝方法:
我的主页:晴天qt01的博客_CSDN博客-数据分析师领域博主
CART分类树算法
-CART分类树的字段选择方法、CART分类树的剪枝作法。
CART(classification and Regression Tree)是一种建构二元分类回归树的算法
二元代表:分支固定,只能是2。能做分类树也能做回归树。
1984年Breiman,Friedman,Olsshen,stone所提出的分类树方法
它的基本逻辑和ID3和C4.5是相同的
主要是字段选择依据和剪枝方法与它们不同,它既不是用information gain 也不是用gain ritio
而是使用Gini index来作为字段选择依据(指标)
剪枝方法上,Bottom-up从上往下进行处理。但是它是配合验证数据集(validation data)用一个非常复杂的公式,来验证训练数据的错误率。而不是使用训练数据观察到的数据集来当错误率。
CART要将训练数据的一部分,拿出来但验证数据集。用验证数据集的真正错误率来评估。
CART字段选择依据
我们用案例来看:
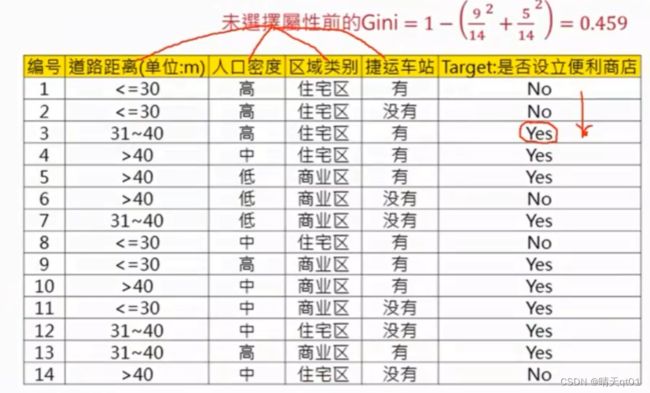
Gini公式很简单就是1-(类别占总体比例的平方之和)。它的数值是在0~0.5之间。越接近0.5,数值就越平均,越靠近0就越偏向某一类。比如全是同一类的时候,1-1=0,如果是一半一半就是1-1/4-1/4.
这个公式有与entropy有类似的功能,但是计算量小了很多对比log来说。所以这个会比较快。
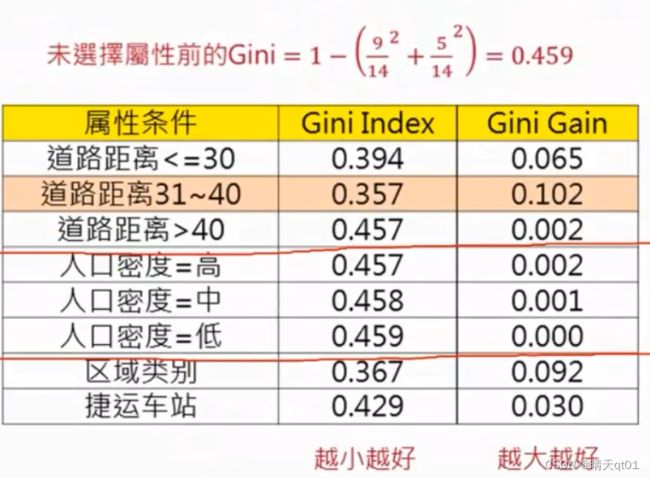
我们可以算出这个基础Gini值为0.459
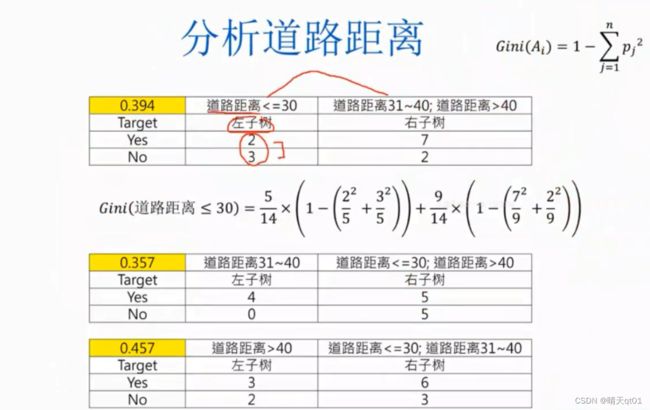
我们看第一个表格,算出第一次计算的Gini index的值是0.394,公式就是‘左子树’的比例乘gini值加上‘右子树’的比例乘以gini值。
那么这里我们对比最小的gini值就可以发现道路距离字段以第2个的分类为代表比较合适比较合适。
之前我们要考虑分类度的问题,CART只考虑2个分支,就可以忽略这一点。
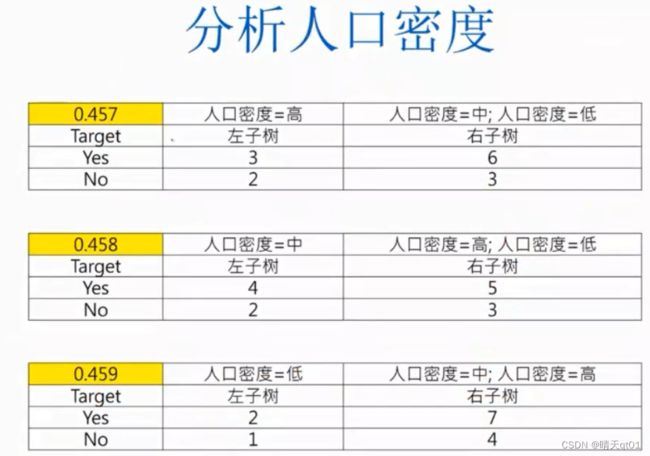
然后我们就可以选出人口密度的字段代表
我们就算出3个gini值,都差不多。
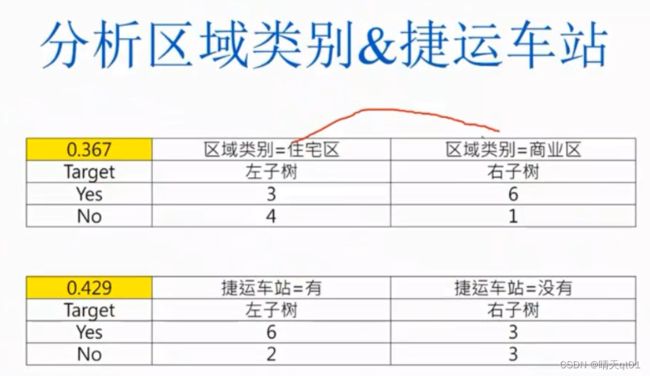
区域类别和便携车站都刚好只有2个那就不用选择了。
总结。
Gini gain是原来的gini值减去后来gini Index的值。
我们依据这个总表来选择需要的字段。:
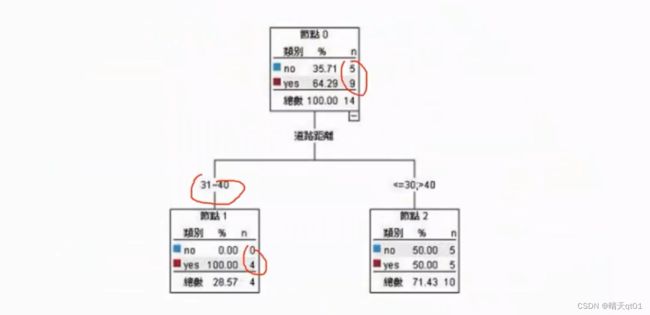
第一个字段就选择,最小gini值的到了距离31~40
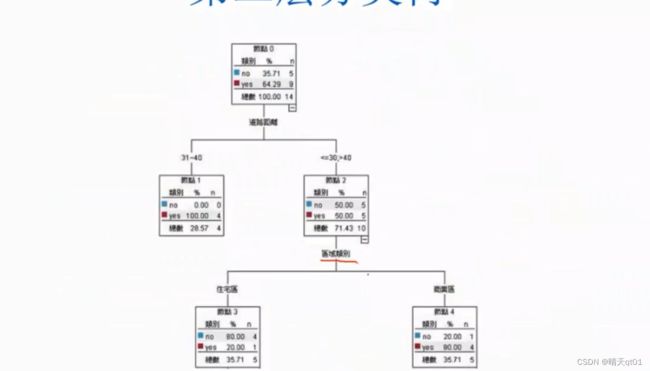
第二个字段就选择区域类别,因为它的gini值第二小
后面为了完全分类正确又可以展开2层
CART分类树的剪枝作法
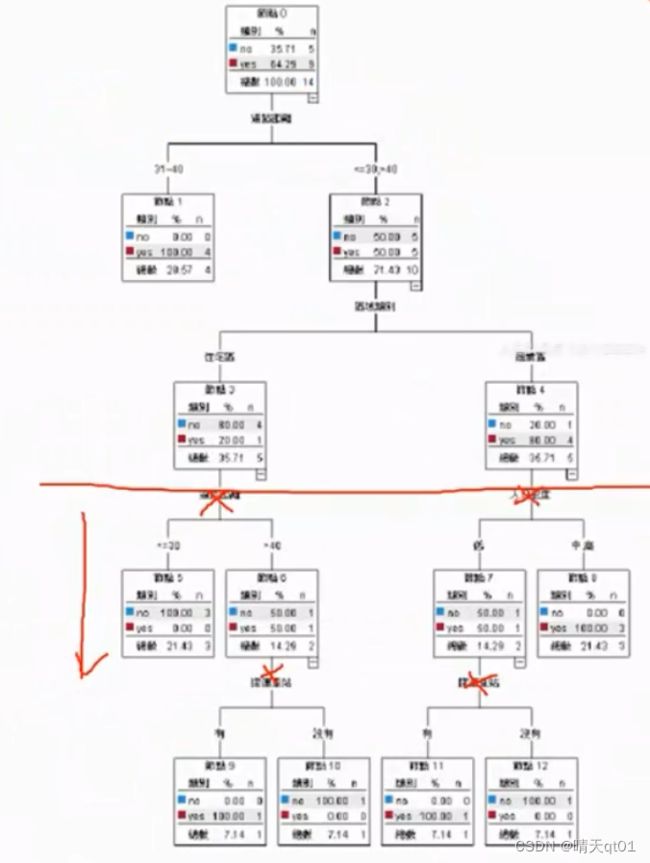
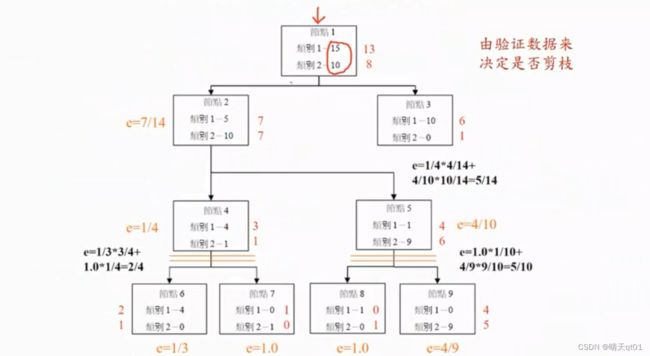
这个时候我们就可以考虑要不要把下面这些剪枝掉,因为我们明显可以看出的笔数很少,数据支撑依据不大。我们要由验证数据集来进行剪枝。
从下面的图可以看出来,结果全部的分类,训练数据集的准确率是百分百。然后我们把验证数据集放进来。
节点的错误率,是验证数据集的错误率。 预测结果是训练数据集的结果,错误率也是看训练数据集的结果。
节点错误率是加权得来的比如左下角的错误率是比例乘以错误率的求和
展开之后错误率的2/4,不展开错误率是1/4.所以不如不展开。
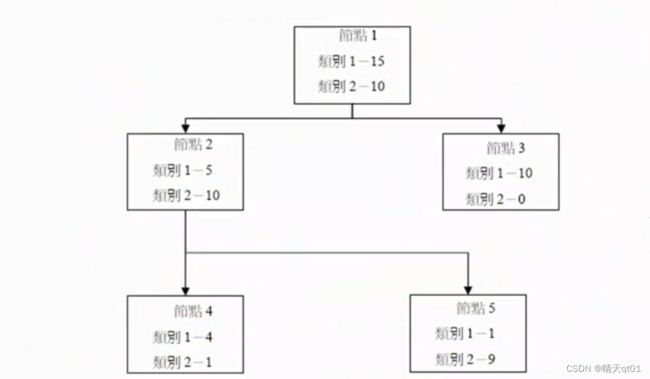
最后剪枝结果如下:
CART处理连续型变量:
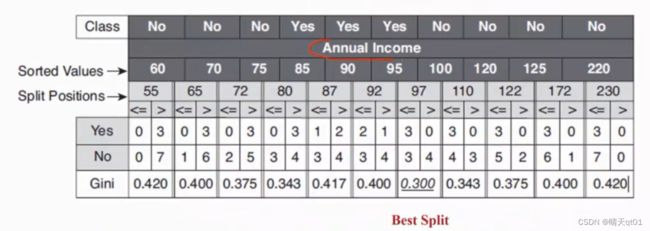
CART处理连续型变量是和C4.5是一样的。
这里有10个数据,所以我们就用10个数据的每个节点来作为分隔处理。求出其中最小的gini值,这里面我就以97为处理分隔的依据。
CHAID分类树算法
-CHAID的字段选择方式
CHAID是由统计学家提出的方法,字段选择方式它用的是卡方统计量。
卡方分布其实就是针对两个类别型字段是否分布相同。
而数值型字段,它会帮你自动离散化,变成类别型字段之后,分析它是否与目标字段有关。越大说明关系越显著,否则不明显。
案例:
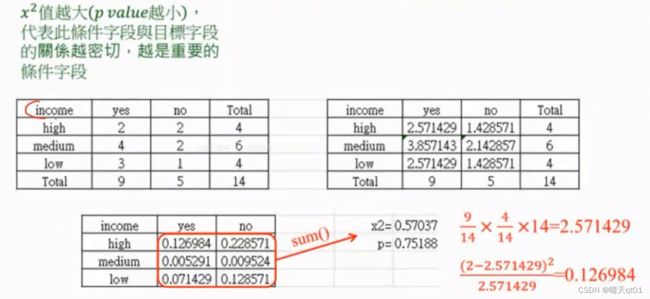
上表的列是收入高低,列是是否买电脑。
卡方统计量的计算,要先从数据里得出出现频次,然后再求出各自的期望。然后求二者的差值。进行求和
第二个求期望的表格,就相当于是认为二者独立,所以可以直接用二者的概率相乘,然后乘以总计。
如果左边的字段与右边的字段越像,就说明二者的关系越薄弱。
第三个表格就是求方差。求和之后,x2等于0.57,对应的概率为75%
说明二者比较薄弱。
我们计算一下全部的卡方概率
这里面的值肯定是越大越好,所以我们就会优先选择年龄作为分类的字段。
剪枝方法:
它会一直让树成长,但是如果P值过大,那么他就直接停止,所以是剪枝方法二从上到下的剪枝方法。Top-dowm
到目前为止,已经把我认为决策树中重要的分类树说完了,下面我们会说到回归树的算法