图解机器学习算法(6) | 决策树模型详解（机器学习通关指南·完结）

• 作者：韩信子@ShowMeAI
• 教程地址：http://www.showmeai.tech/tutorials/34
• 本文地址：http://www.showmeai.tech/article-detail/190
• 声明：版权所有，转载请联系平台与作者并注明出处

---

引言

决策树（Decision Tree）是机器学习中一种经典的分类与回归算法。在本篇中我们讨论用于分类的决策树的原理知识。决策树模型呈树形结构，在分类问题中，一颗决策树可以视作 if-then 规则的集合。模型具有可读性，分类速度快的特点，在各种实际业务建模过程中广泛使用。

（本篇内容会涉及到不少机器学习基础知识，没有先序知识储备的宝宝可以查看ShowMeAI的文章 图解机器学习 | 机器学习基础知识。

1.决策树算法核心思想

1）决策树结构与核心思想

决策树（Decision tree）是基于已知各种情况（特征取值）的基础上，通过构建树型决策结构来进行分析的一种方式，是常用的有监督的分类算法。

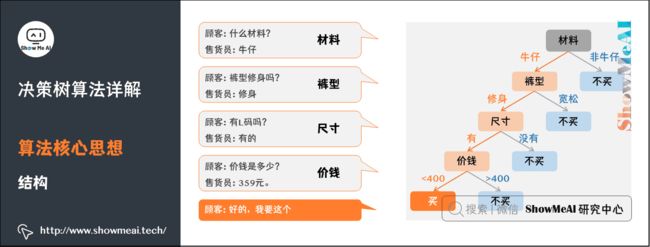
决策树模型（Decision Tree model）模拟人类决策过程。以买衣服为例，一个顾客在商店买裤子，于是有了下面的对话：

决策树是一种预测模型，代表的是对象属性与对象值之间的映射关系。决策树是一种树形结构，其中：

• 每个内部结点表示一个属性的测试
• 每个分支表示一个测试输出
• 每个叶结点代表一种类别

如上图买衣服的例子，第一个「内部结点」对应于属性「材料」上的测试，两个分支分别是该属性取值为「牛仔」和「非牛仔」两种可能结果。当取值为「牛仔」时，则对下个属性「裤型」进行测试；若取值为「非牛仔」时，则对应于「叶结点」——「不买」。

决策树模型核心是下面几部分：

• 结点和有向边组成。
• 结点有内部结点和叶结点俩种类型。
• 内部结点表示一个特征，叶结点表示一个类。

2）决策树的发展史

决策树在发展过程中，有过很多不同类型的模型，典型的模型如ID3、C4.5和CART等，下面我们来简单介绍一下发展史中不同的模型。

2.决策树生长与最优属性的选择

上面介绍的决策树发展史里，大家对于不同的决策树模型有一个基础的理解了，下面一部分，我们来一起看一下决策树是如何生长构成的。

1）决策树生长流程

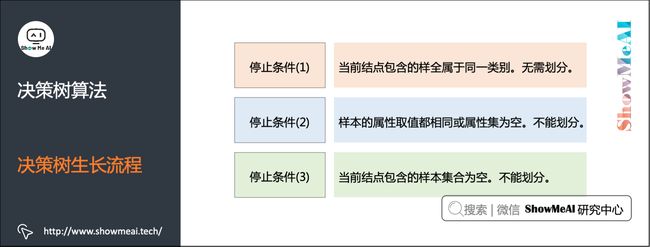
决策树的决策过程就是从根结点开始，测试待分类项中对应的特征属性，并按照其值选择输出分支，直到叶子结点，将叶子结点的存放的类别作为决策结果。简单说来，决策树的总体流程是自根至叶的递归过程，在每个中间结点寻找一个「划分」（split or test）属性。

如下图的伪代码，是详细的决策树生长（构建）流程。大家可以特别注意图中3类终止条件和返回的结果，而整个流程中，有非常核心的一步是「最优划分属性的选择」。

决策树停止生长的三个条件：

2）最优属性选择

下面我们来看看，决策树的最优划分属性选择，是怎么做的。

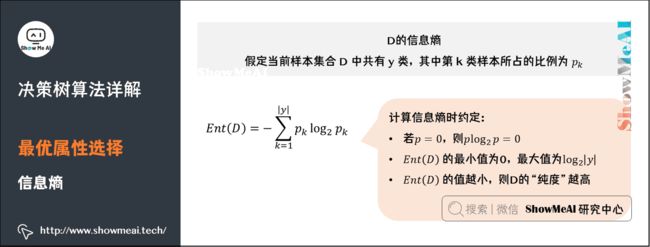
（1）信息熵

要了解决策树的「最优属性」选择，我们需要先了解一个信息论的概念「信息熵（entropy）」（相关知识可以参考ShowMeAI文章 图解AI数学基础 | 信息论），它是消除不确定性所需信息量的度量，也是未知事件可能含有的信息量，可以度量样本集合「纯度」。

对应到机器学习中，假定当前数据集$D$中有$y$类，其中第$k$类样本占比为$p_k$，则信息熵的计算公式如下：

$$Ent(D)=-\sum _{K=1}^{|y|}{p}_k{\log }_2{p}_k$$

但$p_k$取值为1的时候，信息熵为0（很显然这时候概率1表示确定事件，没有任何不确定性）；而当$p_k$是均匀分布的时候，信息熵取最大值$\log (|y|)$（此时所有候选同等概率，不确定性最大）。

（2）信息增益

大家对信息熵有了解后，我们就可以进一步了解信息增益（Information Gain），它衡量的是我们选择某个属性进行划分时信息熵的变化（可以理解为基于这个规则划分，不确定性降低的程度）。

$$\mathrm{Gain}(D,a)=\mathrm{Ent}(D)-\sum _{v=1}^v\frac{\left|D^v\right|}{|D|}\mathrm{Ent}\left(D^v\right)$$

信息增益描述了一个特征带来的信息量的多少。在决策树分类问题中，信息增益就是决策树在进行属性选择划分前和划分后的信息差值。典型的决策树算法ID3就是基于信息增益来挑选每一节点分支用于划分的属性（特征）的。

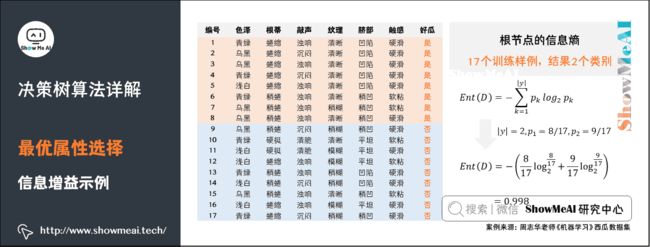
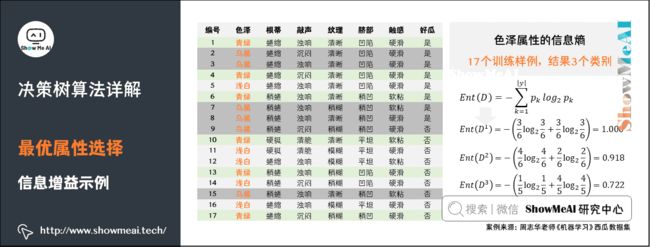
这里以西瓜数据集为例。

• 数据集分为好瓜、坏瓜，所以 $|y|=2$。
• 根结点包含17个训练样例，其中好瓜共计8个样例，所占比例为8/17。
• 坏瓜共计9个样例，所占比例为9/17。

将数据带入信息熵公式，即可得到根结点的信息熵。

以属性「色泽」为例，其对应的3个数据子集：

• $D1(色泽=青绿)$，包含{1,4,6,10,13,17}，6个样例，其中好瓜样例为$\left\{1,4,6\right\}$，比例为3/6，坏瓜样例为$\left\{10,13,17\right\}$，比例为3/6。将数据带入信息熵计算公式即可得到该结点的信息熵。

• $D2(色泽=乌黑)$，包含$\left\{2,3,7,8,9,15\right\}$，6个样例，其中好瓜样例为$\left\{2,3,7,8\right\}$，比例为4/6，坏瓜样例为$\left\{9,15\right\}$，比例为2/6。将数据带入信息熵计算公式即可得到该结点的信息熵。

• $D3(色泽=浅白)$，包含$\left\{5,11,12,14,16\right\}$，5个样例，其中好瓜样例为$\left\{5\right\}$，比例为1/5，坏瓜样例为$\left\{11,12,14,16\right\}$，比例为4/5。将数据带入信息熵计算公式即可得到该结点的信息熵。

色泽属性的信息增益为：

同样的方法，计算其他属性的信息增益为：

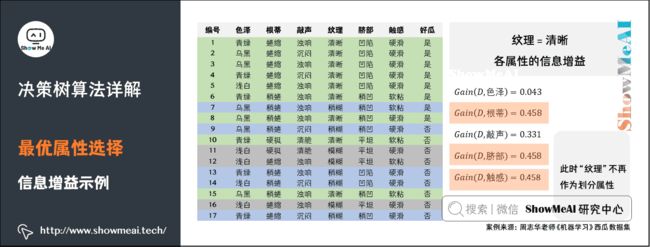
对比不同属性，我们发现「纹理」信息增益最大，其被选为划分属性：清晰$\left\{1,2,3,4,5,6,8,10,15\right\}$、稍糊$\left\{7,9,13,14,17\right\}$、模糊$\left\{11,12,16\right\}$。

再往下一步，我们看看「纹理」=「清晰」的节点分支，该节点包含的样例集合D1中有编号为$\left\{1,2,3,4,5,6,8,10,15\right\}$共计9个样例，可用属性集合为$\left\{色泽,根蒂,敲声,脐部,触感\right\}$（此时「纹理」不再作为划分属性），我们同样的方式再计算各属性的信息增益为：

从上图可以看出「根蒂」、「脐部」、「触感」3个属性均取得了最大的信息增益，可用任选其一作为划分属性。同理，对每个分支结点进行类似操作，即可得到最终的决策树。

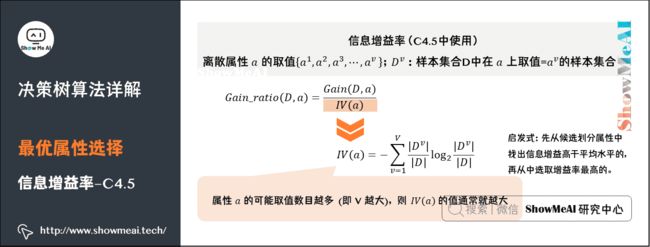
（3）信息增益率（Gain Ratio）

大家已经了解了信息增益作为特征选择的方法，但信息增益有一个问题，它偏向取值较多的特征。原因是，当特征的取值较多时，根据此特征划分更容易得到纯度更高的子集，因此划分之后的熵更低，由于划分前的熵是一定的。因此信息增益更大，因此信息增益比较偏向取值较多的特征。

那有没有解决这个小问题的方法呢？有的，这就是我们要提到信息增益率（Gain Ratio），信息增益率相比信息增益，多了一个衡量本身属性的分散程度的部分作为分母，而著名的决策树算法C4.5就是使用它作为划分属性挑选的原则。

信息增益率的计算细节如下所示：

$${\mathrm{Gain}}_{-}\mathrm{ratio}(D,a)=\frac{\mathrm{Gain}(D,a)}{\mathrm{IV}(a)}$$

$$IV(a)=-\sum _{v=1}^V\frac{\left|D^v\right|}{|D|}{\log }_2\frac{\left|D^v\right|}{|D|}$$

数学上用于信息量（或者纯度）衡量的不止有上述的熵相关的定义，我们还可以使用基尼指数来表示数据集的不纯度。基尼指数越大，表示数据集越不纯。

基尼指数（Gini Index）的详细计算方式如下所示：

$$\mathrm{Gini}(D)=\sum _{k=1}^{|y|}\sum _{k\prime \ne k}{p}_k{p}_{k^{\prime }}=1-\sum _{k=1}^{|y|}{p}_k^2$$

其中，$p_k$表示第$k$类的数据占总数据的比例，著名的决策树算法CART就是使用基尼指数来进行划分属性的挑选（当然，CART本身是二叉树结构，这一点和上述的ID3和C4.5不太一样）。

对于基尼指数的一种理解方式是，之所以它可以用作纯度的度量，大家可以想象在一个漆黑的袋里摸球，有不同颜色的球，其中第k类占比记作$p_k$，那两次摸到的球都是第k类的概率就是$p_k^2$，那两次摸到的球颜色不一致的概率就是$1-\Sigma p_k^2$，它的取值越小，两次摸球颜色不一致的概率就越小，纯度就越高。

3.过拟合与剪枝

如果我们让决策树一直生长，最后得到的决策树可能很庞大，而且因为对原始数据学习得过于充分会有过拟合的问题。缓解决策树过拟合可以通过剪枝操作完成。而剪枝方式又可以分为：预剪枝和后剪枝。

1）决策树与剪枝操作

为了尽可能正确分类训练样本，有可能造成分支过多，造成过拟合。过拟合是指训练集上表现很好，但是在测试集上表现很差，泛化性能差。可以通过剪枝主动去掉一些分支来降低过拟合的风险，并使用「留出法」进行评估剪枝前后决策树的优劣。

基本策略包含「预剪枝」和「后剪枝」两个：

• 预剪枝（pre-pruning）：在决策树生长过程中，对每个结点在划分前进行估计，若当前结点的划分不能带来决策树泛化性能的提升，则停止划分并将当前结点标记为叶结点。

• 后剪枝（post-pruning）：先从训练集生成一颗完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能的提升，则将该子树替换为叶结点。

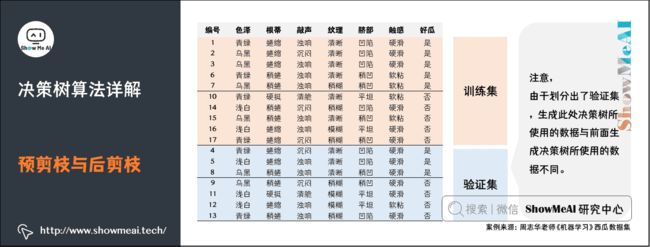
2）预剪枝与后剪枝案例

我们来看一个例子，下面的数据集，为了评价决策树模型的表现，会划分出一部分数据作为验证集。

在上述西瓜数据集上生成的一颗完整的决策树，如下图所示。

（1）预剪枝

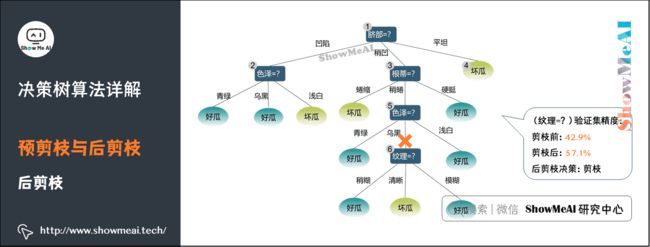
「预剪枝」过程如下：将其标记为叶结点，类别标记为训练样例中最多的类别。

• 若选「好瓜」，验证集中{4,5,8}被分类正确，得到验证集精度为3/7x100%=42.9%

• 根据结点②③④的训练样例，将这3个结点分别标记为「好瓜」、「好瓜」、「坏瓜」。此时，验证集中编号为{4,5,8,11,12}的样例被划分正确，验证集精度为5/7x100%=71.4%

  • 结点2（好瓜）：分类正确：{4,5}，分类错误：{13}
  • 结点3（好瓜）：分类正确：{8}，分类错误：{9}
  • 结点4（坏瓜）：分类正确：{11,12}

若划分后的验证集精度下降，则拒绝划分。对结点②③④分别进行剪枝判断，结点②③都禁止划分，结点④本身为叶子结点。

根据预剪枝方法，此处生成了一层决策树。这种最终得到仅有一层划分的决策树，称为「决策树桩」（decision stump）。

（2）后剪枝

我们在生成的完整决策树上进行「后剪枝」：

• 用验证集的数据对该决策树进行评估，样例$\left\{4,11,12\right\}$分类正确，而样例$\left\{5,8,9,13\right\}$分类错误，此时的精度为42.9%。

• 当对该决策树进行后剪枝，结点⑥的标记为好瓜，此时样例$\left\{4,8,11,12\right\}$分类正确，样例$\left\{5,9,13\right\}$分类错误，精度为57.1%。

剪枝后的精度提升了，因此该决策树需要在结点⑥处进行剪枝。

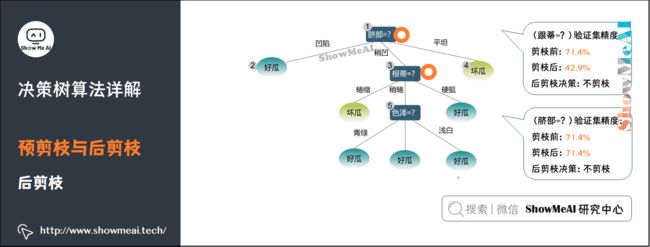
考虑结点⑤，若将其替换为叶结点，根据落在其上的训练样例$\left\{6,7,15\right\}$将其标记为「好瓜」，测得验证集精度仍为57.1%，可以不剪枝。

考虑结点②，若将其替换为叶结点，根据落在其上的训练样例$\left\{1,2,3,14\right\}$将其标记为「好瓜」，测得验证集精度提升至71.4%，决定剪枝。

对结点③和①，若将其子树替换为叶结点，则所得决策树的验证集精度分布为71.4%和42.9%，均未提高，所以不剪枝。得到最终后剪枝之后的决策树。

3）预剪枝与后剪枝的特点

时间开销：

• 预剪枝：训练时间开销降低，测试时间开销降低。
• 后剪枝：训练时间开销增加，测试时间开销降低。

过/欠拟合风险：

• 预剪枝：过拟合风险降低，欠拟合风险增加。
• 后剪枝：过拟合风险降低，欠拟合风险基本不变。

泛化性能：后剪枝通常优于预剪枝。

4.连续值与缺失值的处理

1）连续值处理

我们用于学习的数据包含了连续值特征和离散值特征，之前的例子中使用的都是离散值属性（特征），决策树当然也能处理连续值属性，我们来看看它的处理方式。

对于离散取值的特征，决策树的划分方式是：选取一个最合适的特征属性，然后将集合按照这个特征属性的不同值划分为多个子集合，并且不断的重复这种操作的过程。

对于连续值属性，显然我们不能以这些离散值直接进行分散集合，否则每个连续值将会对应一种分类。那我们如何把连续值属性参与到决策树的建立中呢？

因为连续属性的可取值数目不再有限，因此需要连续属性离散化处理，常用的离散化策略是二分法，这个技术也是C4.5中采用的策略。

具体的二分法处理方式如下图所示：

注意：与离散属性不同，若当前结点划分属性为连续属性，该属性还可以作为其后代结点的划分属性。

2）缺失值处理

原始数据很多时候还会出现缺失值，决策树算法也能有效的处理含有缺失值的数据。使用决策树建模时，处理缺失值需要解决2个问题：

• Q1：如何进行划分属性选择？

• Q2：给定划分属性，若样本在该属性上的值缺失，如何进行划分？

缺失值处理的基本思路是：样本赋权，权重划分。我们来通过下图这份有缺失值的西瓜数据集，看看具体处理方式。

仅通过无缺失值的样例来判断划分属性的优劣，学习开始时，根结点包含样例集 D 中全部17个样例，权重均为1。

• 根结点选择「色泽」属性时，有3个缺失值，因此样例总数为14。

• 此时好瓜样例为$\left\{2,3,4,6,7,8\right\}$，比例为6/14，坏瓜样例为$\left\{9,10,11,12,14,15,16,17\right\}$，比例为8/14。

将数据带入信息熵计算公式即可得到该结点的信息熵。

令$\widetilde{D^1}$、$\widetilde{D^2}$、$\widetilde{D^3}$分别表示在属性「色泽」上取值为「青绿」「乌黑」以及「浅白」的样本子集：

• $\widetilde{D^1}(色泽=青绿)$，包含$\left\{4,6,10,17\right\}$，4个样例，其中好瓜样例为$\left\{4,6\right\}$，比例为2/4，坏瓜样例为$\left\{10,17\right\}$，比例为2/4。将数据带入信息熵计算公式即可得到该结点的信息熵。

• $\widetilde{D^2}(色泽=乌黑)$，包含$\left\{2,3,7,8,9,15\right\}$，6个样例，其中好瓜样例为$\left\{2,3,7,8\right\}$，比例为4/6，坏瓜样例为$\left\{9,15\right\}$，比例为2/6。将数据带入信息熵计算公式即可得到该结点的信息熵。

• $\widetilde{D^3}(色泽=浅白)$，包含$\left\{11,12,14,16\right\}$，4个样例，其中好瓜样例为$\left\{\varphi \right\}$，比例为0/5，坏瓜样例为$\left\{11,12,14,16\right\}$，比例为4/4。将数据带入信息熵计算公式即可得到该结点的信息熵。

于是，样本集D上属性「色泽」的信息增益可以计算得出，Gain(D,纹理)=0.424信息增益最大，选择「纹理」作为接下来的划分属性。

更多监督学习的算法模型总结可以查看ShowMeAI的文章 AI知识技能速查 | 机器学习-监督学习。

视频教程

可以点击 B站 查看视频的【双语字幕】版本

【双语字幕+资料下载】MIT 6.036 | 机器学习导论(2020·完整版)

【双语字幕+资料下载】MIT 6.036 | 机器学习导论(2020·完整版)

https://www.bilibili.com/video/BV1y44y187wN?p=12

ShowMeAI图解机器学习算法系列（完整版）

• ShowMeAI 图解机器学习算法(1) | 机器学习基础知识
• ShowMeAI 图解机器学习算法(2) | 模型评估方法与准则
• ShowMeAI 图解机器学习算法(3) | KNN算法及其应用
• ShowMeAI 图解机器学习算法(4) | 逻辑回归算法详解
• ShowMeAI 图解机器学习算法(5) | 朴素贝叶斯算法详解
• ShowMeAI 图解机器学习算法(6) | 决策树模型详解
• ShowMeAI 图解机器学习算法(7) | 随机森林分类模型详解
• ShowMeAI 图解机器学习算法(8) | 回归树模型详解
• ShowMeAI 图解机器学习算法(9) | GBDT模型详解
• ShowMeAI 图解机器学习算法(10) | XGBoost模型最全解析
• ShowMeAI 图解机器学习算法(11) | LightGBM模型详解
• ShowMeAI 图解机器学习算法(12) | 支持向量机模型详解
• ShowMeAI 图解机器学习算法(13) | 聚类算法详解
• ShowMeAI 图解机器学习算法(14) | PCA降维算法详解

ShowMeAI系列教程精选推荐

• 大厂技术实现：推荐与广告计算解决方案
• 大厂技术实现：计算机视觉解决方案
• 大厂技术实现：自然语言处理行业解决方案
• 图解Python编程：从入门到精通系列教程
• 图解数据分析：从入门到精通系列教程
• 图解AI数学基础：从入门到精通系列教程
• 图解大数据技术：从入门到精通系列教程
• 图解机器学习算法：从入门到精通系列教程
• 机器学习实战：手把手教你玩转机器学习系列
• 深度学习教程：吴恩达专项课程 · 全套笔记解读
• 自然语言处理教程：斯坦福CS224n课程 · 课程带学与全套笔记解读
• 深度学习与计算机视觉教程：斯坦福CS231n · 全套笔记解读