【深度学习基础】从零开始的炼丹生活09——循环神经网络
往期回顾:
06——深度学习中的正则化
07——深度模型中的优化
08——卷积网络
为了处理一维序列数据,我们转向神经网络框架中另一强大的特化,循环神经网络。(主要参考《深度学习》和cousera上吴恩达的课程)
循环神经网络(recurrent neural network)或 RNN ,是一类用于处理序列数据的神经网络。大多数循环网络都能处理可变长度的序列。循环网络强调参数共享,这使得模型能够扩展到不同形式的样本并进行泛化。例如 “我八点吃的早饭” 和 “我早饭在八点吃” ,要提取时间信息。如果我们训练一个前馈网络,需要分别学习句子每个位置的所有语言规则,而循环网络在几个时间步内共享相同的权重,不需要在每个位置都分别学习。

循环网络的计算图有两种表现方式,如图。左边循环图展开后就是右边展开图。
一、循环神经网络
RNN 的设计模式主要有以下几种:
- 每个时间步都有输出,并且隐藏单元之间有循环连接的循环网络。如图:
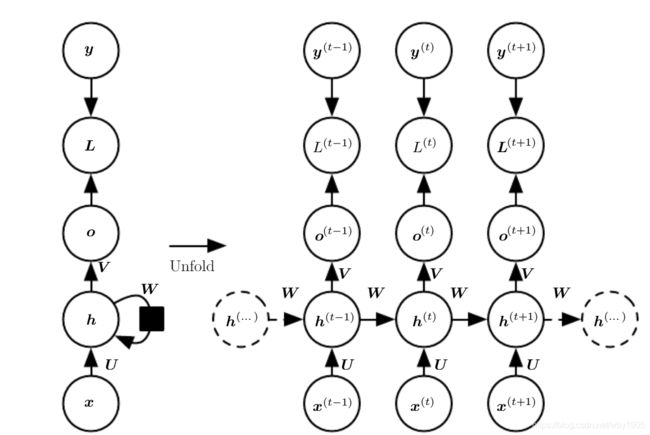
- 每个时间步产生一个输出,只有当前时刻的输出到下个时刻的隐藏单元之间有循环连接的循环网络。如图:

- 隐藏单元之间存在循环连接,读取整个序列后产生单个输出的循环网络,如图:
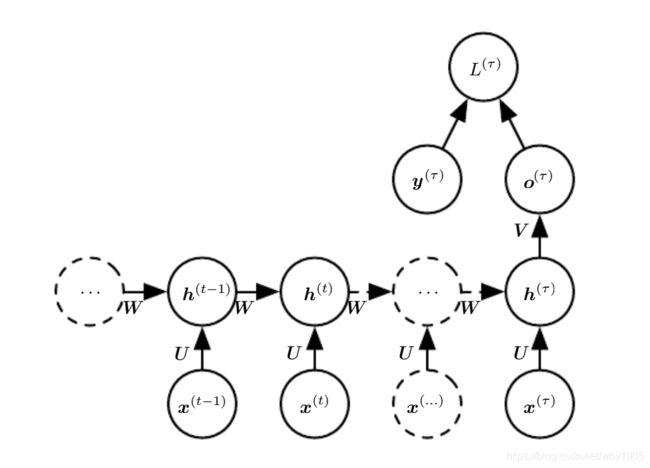
现在我们研究第一种情形的 RNN 前向传播公式。这种循环网络可以计算任何图灵可计算的函数。我们使用 tanh 作为激活函数,RNN 从特定的初始状态 h ( 0 ) \boldsymbol h^{(0)} h(0)出发,开始前向传播。从 t = 1 t=1 t=1 到 t = τ t=\tau t=τ 的每个时间步,我们应用以下更新方程: a ( t ) = b + W h ( t − 1 ) + U x ( t ) h ( t ) = tanh ( a ( t ) ) o ( t ) = c + V h ( t ) y ^ ( t ) = softmax ( o ( t ) ) \begin{aligned}\boldsymbol a^{(t)} &= \boldsymbol{b+Wh^{(t-1)}+Ux^{(t)}}\\ \boldsymbol h^{(t)}&=\boldsymbol{\tanh(a^{(t)})}\\ \boldsymbol o^{(t)}&=\boldsymbol {c +Vh^{(t)}}\\ \boldsymbol {\hat y^{(t)}}&=\text{softmax}(\boldsymbol o^{(t)}) \end{aligned} a(t)h(t)o(t)y^(t)=b+Wh(t−1)+Ux(t)=tanh(a(t))=c+Vh(t)=softmax(o(t))这个循环网络将一个输入序列映射到相同长度的输出序列。与 x \boldsymbol x x 序列配对的 y \boldsymbol y y 的总损失就是所有时间步的损失之和。例如, L ( t ) L^{(t)} L(t) 为给定的 x ( 1 ) , … , x ( t ) \boldsymbol {x^{(1)},\dots,x^{(t)}} x(1),…,x(t) 后 y ( t ) \boldsymbol y^{(t)} y(t) 的负对数似然,则: L ( { x ( 1 ) , … , x ( τ ) } , { y ( 1 ) , … , y ( τ ) } ) = ∑ t L ( t ) = − ∑ t log p model ( y ( t ) ∣ { x ( 1 ) , … , x ( t ) } ) \begin{aligned} L &\big (\{\boldsymbol {x^{(1)},\dots,x^{(\tau)}}\},\{\boldsymbol {y^{(1)},\dots,y^{(\tau)}}\}\big)\\ &=\sum_tL^{(t)}\\ &=-\sum_t\log p_\text{model}(y^{(t)}|\{\boldsymbol {x^{(1)},\dots,x^{(t)}}\})\end{aligned} L({x(1),…,x(τ)},{y(1),…,y(τ)})=t∑L(t)=−t∑logpmodel(y(t)∣{x(1),…,x(t)})
关于各个参数计算这个损失函数的梯度计算成本很高,因为它不能通过并行化来降低,每个时间步只能一前一后的计算。前向传播中各个状态必须保存,以在反向传播中被使用。因此应用于展开图且代价为 O ( τ ) \mathcal O(\tau) O(τ) 的反向传播算法称为通过时间反向传播(back-propagation through time, BPTT),所以隐藏单元之间存在循环的网络非常强大但训练代价也很大。
导师驱动过程和输出循环网络
对于第二种情形,仅在一个时间步的输出和下一个时间步的隐藏单元间存在循环连接的网络确实没有第一种那么强大,因为缺乏隐藏到隐藏的循环连接。例如,它不能模拟通用图灵机。但消除了隐藏到隐藏循环使得任何基于比较时刻 t 的预测和时刻 t 的训练目标的损失函数中的所有时间步都解耦了。使得训练可以并行化。因为训练集提供了输出的理想值,因此没有必要先计算前一时刻的输出。
由输出反馈的模型的循环连接模型可用**导师驱动过程(teacher forcing)**进行训练。如图:
训练时我们将训练集中正确的输出反馈到下一个时间步。而当模型部署后,我们用模型的输出近似正确的输出,并反馈回模型。这样可以避免通过时间来传播。
当然,只要模型一个时间步的输出与下一时间步计算的值存在连接,导师驱动过程就可以使用。因此某些模型要同时使用导师驱动和 BPTT 。
如果之后网络在闭环中使用,即上图的循环连接,完全使用导师驱动会出现缺点,训练期间网络看到的输入和测试时看到的有很大的不同。一种解决方法是同时使用导师驱动和自由运行的输入进行训练。另一种方式是通过随意选择生成值或真实的数据值作为输入以减小训练时和测试时看到的输入之间的差别。这种方法利用了课程学习策略。
二、双向 RNN
之前我们所说的 RNN 都是在时刻 t 的状态只能从过去的序列以及当前的输入中捕获信息,但是在许多情况下,我们要输出的 y ( t ) \boldsymbol y^{(t)} y(t) 的预测可能依赖于整个输入序列。
双向循环神经网络就是为此发明的。它在需要双向信息的应用中很成功。双向 RNN 结合时间上从序列起点开始移动的 RNN 和另一个时间上从序列末尾开始移动的 RNN. 如图:

这允许输出单元能够计算同时依赖于过去和未来且对时刻 t 的输入值最敏感的表示,而不必指定 t 周围固定大小的窗口。
这种思想可以扩展到二维,如图像。由 4 个 RNN 组成,每一个沿着上下左右中的一个方向计算。相比卷积网络,应用于图像的 RNN 计算成本更高,但允许同一特征图的特征之间存在长期横向的相互作用。
三、基于编码 - 解码的序列到序列结构
RNN 可以将输入序列映射成固定大小的向量,也可以将固定大小的向量映射成一个序列,同时之前我们也说了可以将一个输入序列映射到等长的序列。本节讲述如何将输入序列映射到不一定等长的输出序列。这在机器翻译,问答等都有应用。
我们将 RNN 的输入称为“上下文”,我们希望产生上下文的表示 C C C 这个 C C C 可能是一个向量或者向量序列。
用于映射可变长度到另一可变长度序列的 RNN 架构称为编码 - 解码或序列到序列架构,如图:
它的想法很简单:
- 编码器(encoder) 或 读取器(reader) RNN 处理输入序列。输出上下文 C C C (通常是最终隐藏状态)。
- 解码器(decoder) 或 写入器(writer) RNN 以固定长度的向量为条件产生输出序列。
这种架构的两个网络的长度可以不同,两个 RNN 共同训练以最大化 log P ( y ( 1 ) , … , y ( n y ) ∣ x ( 1 ) , … , x ( n x ) ) \log P(\boldsymbol{y^{(1)},\dots,y^{(n_y)}|x^{(1)},\dots,x^{(n_x)}}) logP(y(1),…,y(ny)∣x(1),…,x(nx)) (关于训练集中所有 x 和 y 对的平均)。编码器 RNN 的最后一个状态 h n x \boldsymbol h_{n_x} hnx 通常被当作输入的表示 C C C 并作为解码器 RNN 的输入。
如果 C C C 是一个向量,那么解码器就是之前说的向量到序列 RNN ,它的输入既可以提供为 RNN 的初始状态,或连接到每个时间步的隐藏单元。也可以两种方式结合。
此架构的一个明显不足就是编码器 RNN 的输出上下文 C C C 的维度太小而难以适当地概括一个过长的序列。因此可以让它变为可变长度的序列,由此产生了将序列 C C C 的元素和输出序列的元素相关联的注意力机制(attention mechanism).
关于注意力机制的进一步阅读,请看:
深度学习中的注意力机制
从0到1再读注意力
四、深度循环网络
大多数 RNN 中的计算可以分解为 3 块参数及其相关的变换:
- 从输入到隐藏状态
- 从前一隐藏状态到下一隐藏状态
- 从隐藏状态到输出
将 RNN 的状态分为多层有许多好处,如图: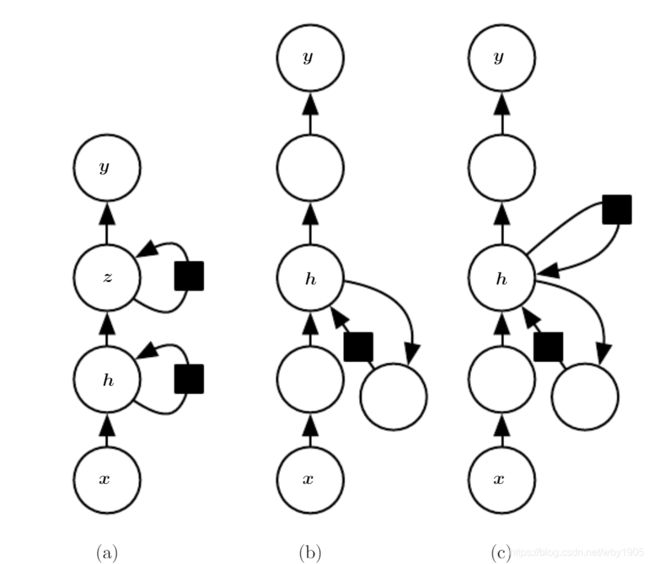
(a)所示层次结构中较低的层起到了将原始输入转化为对更高层的隐藏状态更合适表示的作用。(b) 展示了可以向输入到隐藏、隐藏到隐藏以及隐藏到输出的部分引入更深的计算(如 MLP ),但这会导致优化困难。针对这个问题,提出了©的结构,引入了跳跃连接来缓解路径延长的效应。
五、长期依赖的挑战
经过许多阶段传播后的梯度倾向于消失(大部分情况)或爆炸。循环网络涉及相同函数的多次组合,每个时间步一次,这些组合可能导致很多问题。
一种解决方案是回声状态网络,具体请看
回声状态网络(ESN)原理详解(附源码实现)
还有一种方法是设计工作在多个尺度的模型,使模型的某些部分在细粒度时间尺度上操作并能处理小细节,而其他部分在粗时间尺度上操作并把遥远过去的信息有效地传递。有许多同时构建粗细时间尺度的策略。
1. 时间维度的跳跃连接
增加跳跃连接使得到粗时间尺度的一种方法。但这依然存在延迟和单步连接,使得梯度依然可能随时间指数爆炸。因此不是所有的长期依赖都能在这种方式下良好地表示。
2. 渗漏单元和一系列不同时间尺度
获得导数乘积接近 1 的另一种方式使设置线性自连接单元,使得连接的权重接近 1。线性自连接的隐藏单元可以模拟滑动平均的行为。这种单元称为渗漏单元(leaky unit),它应用更新: μ ( t ) ← α μ ( t − 1 ) + ( 1 − α ) v ( t ) \mu^{(t)}\leftarrow \alpha\mu^{(t-1)}+(1-\alpha)v^{(t)} μ(t)←αμ(t−1)+(1−α)v(t)
d 时间步的跳跃连接可以确保单元总能被 d 个时间步前的那个值影响。使用权重接近 1 的线性自连接是确保该单元可以访问过去值的不同方式。通过调节 α ,可以更平滑的调整记忆效果。
3. 删除连接
另一种方法是在多个时间尺度组织 RNN 状态。它涉及主动删除长度为一的连接并用更长的连接替换。
一种方式是使循环单元变成渗漏单元,但不同的单元组关联不同的固定时间尺度;另一种方式是使显式且离散的更新发生在不同时间,不同的单元组有不同的频率。
六、长短期记忆和其他门控 RNN
实际应用时较为有效的序列模型称为 门控 RNN(gated RNN)。包括基于长短期记忆(long short-term memory) 和基于 门控循环单元(gated recurrent unit) 的网络。
像渗漏单元一样,门控 RNN 想法也是基于生成通过时间的路径,其中的导数既不消失也不爆炸。门控 RNN 将连接权重推广为在每个时间步都可能改变的连接权重。此外,让网络在使用旧的信息后进行遗忘也是很有用的,这也是门控 RNN 所做的事。
1. LSTM
LSTM 引入了自循环的思想,以产生梯度长时间持续流动的路径。且一个关键的扩展是使自循环的权重视上下文而定,而非固定的。 LSTM 除了外部的 RNN 循环外,还具有内部的自环,因此 LSTM 不是简单地向输入和循环单元的仿射变换后施加一个逐元素的非线性。
LSTM 块的基本结构如图(cousera版本):
LSTM 网络比简单的循环架构更易于学习长期依赖。
2. 其他门控 RNN
LSTM 哪些部分是真正必需的?
GRU 给出了一个答案,它与 LSTM 的主要区别就是单个门控单元同时控制遗忘因子和更新状态单元的决定。
更新门像条件渗漏累计器一样可以线性门控任意维度,从而可以选择遗忘或是记住之前的状态。复位门控制当前状态中哪些部分用于计算下一个目标状态,在过去状态和未来状态之间引入了附加的非线性效应。
围绕这一主题可以设计更多的变种。
例如复位门的输出可以在多个隐藏单元间共享,或者,全局门的乘积和一个据部门结合以结合全局控制和局部控制。但是很多变种的性能并没有太大提升,甚至不如原版。
七、外显记忆
智能需要知识并且可以通过学习获取知识,但是知识是不同的并且种类繁多,有些知识是隐含的、潜意识的且难以用语言表达。神经网络擅长存储隐性知识,但它们难以记住事实。有推测称这是因为神经网络缺乏工作存储系统,即类似人类为实现一些目标而明确保存和操作相关信息片段的系统。
为了解决这一问题, Weston et al.(2014) 引入了记忆网络,其中包括一组可以通过寻址机制来访问的记忆单元。 Gaves et al.(2014) 引入的神经图灵自动机,不需要明确地监督指示采取哪些行动而能学习从记忆单元读写任意内容,并通过使用基于内容的软注意机制,允许端到端的训练。

每个记忆单元可以看作是 LSTM 或 GRU 中记忆单元的扩展。不同的是网络输出一个内部状态来选择从哪个单元读取或写入。无论是软或随机硬性的,用于选择一个地址的机制与先前介绍的注意力机制形式相同。
外显记忆可以使得信息和梯度在非常长的持续时间内传播。
扩展阅读:
DeepNLP的表示学习·词嵌入来龙去脉·深度学习(Deep Learning)·自然语言处理(NLP)·表示(Representation)
自然语言处理nlp全领域综述