上采样:
即放大图像。其目的是在更高分辨率的显示设备上。图像放大几乎都是采用内插值方法,即在原有图像像素的基础上在像素点之间采用合适的插值算法插入新的元素。上采样有3种常见的方法:双线性插值(bilinear),反卷积(Transposed Convolution),反池化(Unpooling)。
下采样:
即缩小图像。其目的是1、使得图像符合显示区域的大小;2、生成对应图像的缩略图。
反卷积:
我们首先已经知道,3*3的过滤器用于连接输入矩阵的9个值和输出矩阵的1个值,卷积运算形成了一种多对一的关系。
而反卷积与之相反,反卷积运算形成了一种一对多的关系,它想把矩阵中的1个值和另一个矩阵的9个值联系起来。反卷积不是正向卷积的完全逆过程,因为反卷积只能保证得到的矩阵和原矩阵大小一致,但各元素的值不一定能一致。用一句话来解释反卷积的过程就是:反卷积是一种特殊的正向卷积,先按照一定的比例通过补0来扩大输入图像的尺寸(padding),接着转置过滤器,再进行正向卷积。
在解释反卷积之前,我们先再回顾一下卷积的过程,不过我们把卷积这一步骤再详细的解释一下,那就是如果这是过滤器:
这是输入矩阵:
那么实际上卷积的过程是这样的:
将过滤器转换成稀疏矩阵,也就是这样操作:
因为输入矩阵有4行,所以这个操作也要重复四遍,变成这个样子:
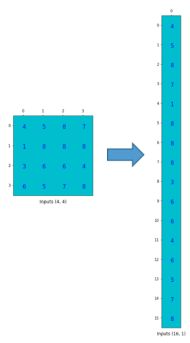
然后输入矩阵需要像全连接层那样变成一列:
最后把稀疏矩阵乘上输入矩阵,就得到了输出矩阵,也就完成了卷积计算。
只需要把这个4*1的列向量,变成2*2的矩阵就可以了!
Fine,这就是卷积的结果,跟以前所认识的是一样的,只不过我们把conv2D拆开看了看它是如何运作的而已。
好了,我们现在可以讲解反卷积了!
既然差不多是逆过程,那么从数学公式来讲,如果输出矩阵是Y,输入矩阵是X,稀疏矩阵是C那么就有:
![]()
实际上刚才所讲的过程已经印证了这个事情,不是吗?好,既然如此,如果我们知道了Y和C,如何求X呢?答案是:
![]()
可能你难以接受,但事实上我们就是这么做的。刚才也说了,反卷积并不能得到与原矩阵一模一样的矩阵,只能得到和原矩阵大小一样的矩阵。
接受了这一点,我们继续讲。按照公式,我们需要将稀疏矩阵转置,然后去乘输出矩阵,这样就得到了输入矩阵。不过同样的,我们也要把Y给变换成正向卷积中的X那样,一列的样子。
老规矩,把得到的列变成矩阵:
wow,amazing,这是我独享的moment!我得到了一个与原矩阵一样大小的矩阵,但是元素却不相同。但它就是这个样子的,这就是反卷积的整个过程了。
通过这个图,可以看到,同一个过滤器,卷积的时候是9对1,反卷积的时候是1对9.