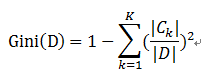【机器学习实战 2】、决策树-ID3-C4.5-CART
机器学习实战,决策树
- 前言
- 一、决策树是什么?
- 二、划分标准—熵
-
- 1、熵
- 2.信息增益(ID3算法)
- 3.信息增益率(C4.5算法)
- 4.基尼指数( CART算法)
- 三、三种算法实现分类
-
- 1、数据集:
- 2、ID3算法:
- 3、Matplotlib注解绘制决策树
- 4、测试ID3算法
- 5、测试C4.5算法
- 6、测试CART算法
- 四、总结
前言
提示:这里可以添加本文要记录的大概内容:
例如:随着人工智能的不断发展,机器学习这门技术也越来越重要,本文介绍决策树,决策树可以使用不熟悉的数据集合,并从中提取出一系列规则,机器学习算法最终将使用决策树(从数据集创造的规则)。
提示:
引用博客
https://www.cnblogs.com/muzixi/p/6566803.html
推荐博客https://blog.csdn.net/zjsghww/article/details/51638126
一、决策树是什么?
决策树 是表示基于特征对实例进行分类的树形结构
从给定的训练数据集中,依据特征选择的准则,递归的选择最优划分特征,并根据此特征将训练数据集进行分割,使得各子数据集有一个最好的分类的过程。
决策树算法3要素:
1、特征选择
2、决策树生成
3、决策树剪枝
1、关于决策树生成
决策树的生成过程就是,选择满足划分准则的特征不断的将数据集划分为纯度更高,不确定性更小的子集的过程。
对于当前数据集D的每一次的划分,都希望根据某特征划分之后的各个子集的纯度更高,不确定性更小。
2、划分标准–特征选择:
目的:
使用某特征对数据集划分之后,各数据子集的纯度要比划分前的数据集D的纯度高(不确定性要比划分前数据集D的不确定性低。)
注意:
1. 划分后的纯度为各数据子集的纯度的加和(子集占比*子集的经验熵)。
2. 度量划分前后的纯度变化 用子集的纯度之和与划分前的数据集D的纯度 进行对比。
特征选择的准则主要有以下三种:信息增益,信息增益率,基尼指数
二、划分标准—熵
了解信息增益前,先了解什么是熵
1、熵
定义为信息的期望值,用来度量信息的不确定性(纯度)
定义:假设随机变量X的可能取值有x1,x2, … , xn
对于每一个可能的取值xi,其概率 P(X=xi) = pi , ( i = 1,2, … , n)
因此随机变量X的熵:
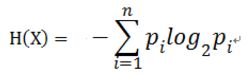
对于样本集合D来说,随机变量X是样本的类别,即,假设样本有k个类别,每个类别的概率是
![]()
其中|Ck|表示类别k的样本个数,|D|表示样本总数
则对于样本集合D来说 熵 为:
D样本集合的不确定性,熵越大
也就可以说熵越大,样本的不确定性就越大。
2.信息增益(ID3算法)
定义: 数据集以某特征划分前后,熵的差值
已经了解到熵越大,样本的不确定性就越大。因此可以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。
信息增益 = entroy(划分前) - entroy(划分后)
书中公式:
![]()
ID3算法:
使用所有特征划分数据集D,计算得到多个特征划分数据集D的信息增益,从这些信息增益中选择最大的特征,将此特征作为树结点开始下一次划分。
缺点:信息增益偏向取值较多的特征
原因:当某特征的取值较多时,根据此特征划分就会有更多次划分,更容易得到纯度更高的子集,因此划分之后的熵更低,由于划分前的熵是一定的,因此信息增益更大,因此信息增益比较偏向取值较多的特征。
3.信息增益率(C4.5算法)
为了解决ID3 的上述缺点,提出信息增益率作为划分标准
信息增益比 = 惩罚参数 * 信息增益
书中公式:
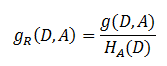
注意:H表示信息熵,g表示信息增益,
其中的HA(D)表示,对于样本集合D,将当前特征A作为随机变量x(取值是特征A的各个特征值),求得的经验熵。
缺点:信息增益率偏向取值较少的特征
原因: 当特征取值较少时HA(D)的值较小,因此其倒数较大,因而信息增益比较大。因而偏向取值较少的特征。
使用信息增益率时,基于以上缺点,并不是直接选择信息增益率最大的特征,而是现在候选特征中找出信息增益高于平均水平的特征,然后在这些特征中再选择信息增益率最高的特征。
4.基尼指数( CART算法)
定义:基尼指数(基尼不纯度):表示在样本集合中一个随机选中的样本被分错的概率。
注意: Gini指数越小表示集合中被选中的样本被分错的概率越小,也就是说集合的纯度越高,反之,集合越不纯。
即 基尼指数(基尼不纯度)= 样本被选中的概率 * 样本被分错的概率
说明:
1. pk表示选中的样本属于k类别的概率,则这个样本被分错的概率是(1-pk)
2. 样本集合中有K个类别,一个随机选中的样本可以属于这k个类别中的任意一个,因而对类别就加和
3. 当为二分类是,Gini§ = 2p(1-p)
样本集合D的Gini指数 : 假设集合中有K个类别,则:
三、三种算法实现分类
1、数据集:
烂尾炎数据集:appendicitis 100条
并拆分为训练集和验证集。
二极管显示数据集:LED7digit 500条
并拆分为训练集和验证集。
2、ID3算法:
使用所有特征划分数据集D,计算得到多个特征划分数据集D的信息增益,从这些信息增益中选择最大的特征,将此特征作为树结点开始下一次划分。
信息增益 = entroy(划分前) - entroy(划分后)
先构建计算熵的函数:
获取数据集的样本个数以计算样本类别概率,然后需要统计每个类别的个数,遍历数据集即可,用字典labelCounts保存。然后即可计算熵
def calcShannonEnt(dataSet):
numEntries = len (dataSet) #先获取数据集的样本个数
labelCounts = {}
for featVec in dataSet: #遍历数据集,统计每个类别的个数
currentLabel = featVec[-1]
if currentLabel not in labelCounts:
labelCounts[currentLabel] = 0
labelCounts[currentLabel] +=1
shannonEnt = 0.0
for key in labelCounts: #计算熵
prob = float(labelCounts[key]) / numEntries
shannonEnt -= prob * log(prob,2)
return shannonEnt
创建数据集,调用函数计算熵
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
calcShannonEnt(dataSet)
#结果为 0.9709505944546686
通过计算信息增益,来选择最佳划分特征,构建下面的函数
伪代码:
首先获取数据的特征个数
计算初始熵
设置最大信息增益为0
按序遍历每个特征
获取每个特征的取值
遍历每个取值
获取特征为对应取值的所有数据,构成子集
对子集计算熵,乘以子集在数据集的比例
将子集的熵累加
计算信息增益
#计算信息增益率。
取最大信息增益
def chooseBestFeatureToSplit(dataSet,flag):
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0;bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
if(flag == 'ratio'):
if(calcfectShannonEnt(dataSet,i) == 0):
infoGain = infoGain/1
else:
infoGain = infoGain/calcfectShannonEnt(dataSet,i)
#print(infoGain)
if(infoGain > bestInfoGain ):
bestInfoGain = infoGain
bestFeature = i
#print(bestFeature)
#print(infoGain)
return bestFeature
划分数据集的函数
伪代码:
遍历数据集:
判断样本对应特征取值是否为value
是,则将该样本中对应特征剔除
将剔除特征后的样本聚集到retDataSet中
返回retDataSet
def splitDataSet(dataSet, axis, value):
retDataSet = []
for featVec in dataSet:
if featVec[axis] ==value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
至此已经完成了从构造决策树算法的子模块,ID3算法的工作原理如下:
获得原始数据集,根据信息增益最大的特征划分数据集。第一次划分结束后,数据将向下传递到子树的一个节点,在这个节点上再次划分数据,可以采用递归的原则处理
递归结束的条件:
遍历完所有特征,或者所有个分支下的所有实例都具有相同的分类,此时得到一个叶子节点。任何到达叶子节点的数据必然属于叶子节点的分类。
如果数据集已经处理了所有的属性,但是类标签依然不是唯一的,此时我们一般采用多数表决的方法决定该叶子节点的分类。。
下面实现生成决策树的代码:
伪代码:
'''
递归生成决策树
:param dataSet: 数据集
:param labels: 标签
:return: 字典形式的决策树
:flag: gain-信息增益 ratio-信息增益率 jini
'''
#获取全部样本的标签v
#如果样本表圈完全相同则停止划分(标签列表中第一个标签的个数等于标签列表个数)
#如果遍历完所有特征是返回出现次数最多的类别
#选择最佳特征
#创建根节点
#删除根节点特征
#获取根节点特征值下的所有制
# 遍历该标签下的值进行划分,构建子树 递归
return myTree
def createTree(dataSet, labels, flag):
'''
递归生成决策树
:param dataSet: 数据集
:param labels: 标签
:return: 字典形式的决策树
:flag: gain-信息增益 ratio-信息增益率 jini
'''
#获取全部样本的标签v
classList = [example[-1] for example in dataSet] # 取标签
#样本表圈完全相同则停止划分(标签列表中第一个标签的个数等于标签列表个数)
if classList.count(classList[0]) == len(classList):
return classList[0]
#如果遍历完所有特征是返回出现次数最多的类别
if len(dataSet[0]) == 1:
return majorityCnt(classList)
#选择最佳特征
bestFeat = chooseBestFeatureToSplit(dataSet, flag) #索引
bestFeatLabel = labels[bestFeat] #值
#创建根节点
myTree = {bestFeatLabel: {}}
# del(labels[bestFeat]) # del 会直接修改原数据 造成 'no surfacing' is not in list 的错误
#删除根节点特征
subLabels = labels[:]
del(subLabels[bestFeat])
#获取根节点特征值下的所有制
featValues = [example[bestFeat] for example in dataSet] # 该特征下的值
uniquevals = set(featValues)
# 根据该标签下的值进行划分 递归
for value in uniquevals:
subLabels = subLabels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels, flag)
return myTree
递归的第二个停止条件是使用完了所有特征,仍然不能将数据集划分成仅含唯一类别的分组,则返回次数最多的类别作为返回值,通过以下函数实现
def majorityCnt(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys():
classCount[vote] = 0
classCount[vote] += 1
sortedClassCount =sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
构建决策树如下
labels = ['no surfacing', 'flippers']
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
myTree = createTree(dataSet,labels,1)
#myTree
#{'flippers': {0: 'no', 1: 'yes'}}
#{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
3、Matplotlib注解绘制决策树
构建绘制决策树所需的函数
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
createPlot.ax1.annotate(nodeTxt, xy=parentPt,
xycoords ='axes fraction',
xytext =centerPt, textcoords ='axes fraction',
va = "center", ha ="center", bbox = nodeType, arrowprops = arrow_args)
def getNumLeafs(myTree):
# 初始化叶节点的计数
numLeafs = 0
# 从myTree的所有节点获取第一个节点(根节点)
firstStr = list(myTree.keys())[0]
# 通过跟节点的key取出根key对应的value
secondDict = myTree[firstStr]
# 遍历根key的value(value包含根key包含的余下所有的子节点)
# 上一级的value包含下一级的key,因此通过递归,可以不断取到下一层的value
for key in secondDict.keys():
# 只要获取到的value的是字典的类型,就进行递归,接着往下取叶节点
if type(secondDict[key]).__name__ == 'dict':
# 每次递归调用该函数都会获取到该节点下的所有叶节点,并进行计数
numLeafs += getNumLeafs(secondDict[key])
# 如果获取的vlaue不再是字典,说明已经是最后一个子节点,进行一次加1操作
else: numLeafs += 1
return numLeafs
def getTreeDepth(myTree):
# 树的层数与获取叶节点的步骤相似,区别在于
# 叶节点数每遍历一次,如果遍历到叶子节点,那么将计数加一,累计叶子节点的个数;
# 树层数的计数在递归的过程中,如果遍历到叶子节点,就会将计数值置为1,只保留max的计数。
# 将这一层的深度记为1
# 初始化一个记录最大深度的变量
maxDepth = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
# 每次递归都进行依次+1的计数操作
thisDepth = 1 + getTreeDepth(secondDict[key])
# 如果没有遍历到dict,只有只有一层
else: thisDepth = 1
# 每一个key对用的子节点串(每一条路径)都会有一个最大值,记录其中最大的那个
if thisDepth > maxDepth: maxDepth = thisDepth
return maxDepth
def plotMidText(cntrPt, parentPt, txtString):
# 分别计算填充文文本位置的x,y坐标
xMid = (parentPt[0] - cntrPt[0])/2.0 + cntrPt[0]
yMid = (parentPt[1] - cntrPt[1])/2.0 + cntrPt[1]
# createPlot方法的ax1属性为一个plot视图,此处为视图添加文本
createPlot.ax1.text(xMid,yMid,txtString)
def plotTree(myTree, parentPt, nodeTxt):
# 获取叶节点数
numleafs = getNumLeafs(myTree)
depth = getTreeDepth(myTree)
# 获取树的第一个key(根节点)
firstStr = list(myTree.keys())[0]
# 子节点的坐标计算
# 子节点 X坐标=节点的x偏移量 + (叶节点数 )
cntrPt = (plotTree.xOff + (1.0 + float(numleafs))/2.0/plotTree.totalW,plotTree.yOff)
# 填充父子节点键的文本
plotMidText(cntrPt, parentPt, nodeTxt)
# 绘制树节点
plotNode(firstStr,cntrPt,parentPt,decisionNode)
# 通过第一个key取获取value
secondDict = myTree[firstStr]
# 树的Y坐标偏移量
plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
# 对比value(所有节点名称,通过节点名称获取到对应的dict)
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
# 如果遍历到字典,将调用本身绘制子节点
plotTree(secondDict[key],cntrPt,str(key))
else: # 已经遍历不到字典,此处已经是最后一个,将其画上
plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
# 绘制子节点
plotNode(secondDict[key],(plotTree.xOff, plotTree.yOff),cntrPt, leafNode)
# 添加节点间的文本信息
plotMidText((plotTree.xOff, plotTree.yOff),cntrPt, str(key))
# 确定y的偏移量
plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
def createPlot(inTree):
fig = plt.figure(1, facecolor='White')
fig.clf()
# 不需要设置x,y的刻度文本
axprops = dict(xticks= [], yticks=[])
# 添加子图
createPlot.ax1 = plt.subplot(111,frameon=False, **axprops)
# 设置plotTree方法中的变量
# 总的宽度 = 叶子节点的数量
plotTree.totalW = float(getNumLeafs(inTree))
# 总的高度 = 树的层数
plotTree.totalD = float(getTreeDepth(inTree))
# 定义plotTree的xOff, yOff属性的初始值
plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0
# 调用plotTree方法
plotTree(inTree, (0.5, 1), '')
plt.show()
生成决策树
data = pd.read_csv("dataset1train.csv",header = None)
data = py.array(data)
data = data.tolist()
labels = ['m1','m2','m3','m4','m5','m6','m7']
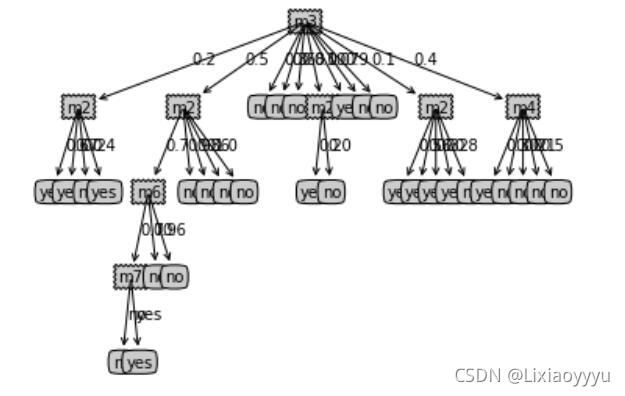
myTree1 = createTree(data,labels,'gain')
createPlot(myTree1)
4、测试ID3算法
依靠训练数据集构造了决策树之后,构建分类函数执行分类。
def classify(inputTrees, featLabels, testVec):
firstStr = list(inputTrees.keys())[0]
secondDict = inputTrees[firstStr]
featIndex = featLabels.index(firstStr) #寻找决策属性在输入向量中的位置
classLabel = -1 #-1是作为flag值
for key in secondDict.keys():
if testVec[featIndex] == key: #如果对应位置的值与键值相等
if type(secondDict[key]).__name__ == 'dict':
#继续递归查找
classLabel = classify(secondDict[key],featLabels, testVec)
else:
classLabel = secondDict[key] #查找到子节点则返回子节点的标签
#标记classLabel为-1当循环过后若仍然为-1,表示未找到该数据对应的节点则我们返回他兄弟节点出现次数最多的类别
return getLeafBestCls(inputTrees) if classLabel == -1 else classLabel
然后由于可能存在找不到对应叶子节点的数据,需要对此处理,返回他兄弟节点出现次数最多的类别,构建以下函数:
#求该节点下所有叶子节点的列表
def getLeafscls(myTree, clsList):
numLeafs = 0
firstStr = list(myTree.keys())[0]
secondDict = myTree[firstStr]
for key in secondDict.keys():
if type(secondDict[key]).__name__ == 'dict':
clsList =getLeafscls(secondDict[key],clsList)
else:
clsList.append(secondDict[key])
return clsList
#返回出现次数最多的类别
def getLeafBestCls(myTree):
clsList = []
resultList = getLeafscls(myTree,clsList)
return max(resultList,key = resultList.count)
计算验证集准确率
def culprecision(inputTree,featLabels,data_test):
count = 0
for example in data_test:
if(classify(inputTree,featLabels,example) == example[-1]):
count +=1
return count/len(data_test)
测试生成的决策树
data = pd.read_csv("dataset1train.csv",header = None)
data = py.array(data)
data = data.tolist()
labels = ['m1','m2','m3','m4','m5','m6','m7']
myTree1 = createTree(data,labels,'gain')
createPlot(myTree1)
data_test = pd.read_csv("dataset1test.csv",header = None)
data_test = py.array(data)
data_test = data_test.tolist()
culprecision(myTree1,labels,data_test)
#precision:0.8117647058823529
5、测试C4.5算法
C4.5参考的划分标准是最大增益率,只需改进ID3算法部分代码即可
1、添加标志 flag 来判断使用ID3还是C4.5
2、同时计算完信息增益后除以对应特征的熵求得信息增益率。
def chooseBestFeatureToSplit(dataSet,flag):
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0;bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy
if(flag == 'ratio'):
if(calcfectShannonEnt(dataSet,i) == 0):
infoGain = infoGain/1
else:
infoGain = infoGain/calcfectShannonEnt(dataSet,i)
#print(infoGain)
if(infoGain > bestInfoGain ):
bestInfoGain = infoGain
bestFeature = i
print(bestFeature)
print(infoGain)
return bestFeature
计算对应特征的熵:
def calcfectShannonEnt(dataSet,i):
numEntries = len (dataSet)
featureCounts = {}
for featVec in dataSet:
currentfeature = featVec[i]
if currentfeature not in featureCounts:
featureCounts[currentfeature] = 0
featureCounts[currentfeature] +=1
shannonEnt = 0.0
for key in featureCounts:
prob = float(featureCounts[key]) / numEntries
shannonEnt -= prob * log(prob,2)
return shannonEnt
生成决策树
def createTree(dataSet, labels, flag):
'''
递归生成决策树
:param dataSet: 数据集
:param labels: 标签
:return: 字典形式的决策树
:flag: gain-信息增益 ratio-信息增益率 jini
'''
#获取全部样本的标签v
classList = [example[-1] for example in dataSet] # 取标签
#样本表圈完全相同则停止划分(标签列表中第一个标签的个数等于标签列表个数)
if classList.count(classList[0]) == len(classList):
return classList[0]
#如果遍历完所有特征是返回出现次数最多的类别
if len(dataSet[0]) == 1:
return majorityCnt(classList)
#选择最佳特征
bestFeat = chooseBestFeatureToSplit(dataSet, flag) #索引
bestFeatLabel = labels[bestFeat] #值
#创建根节点
myTree = {bestFeatLabel: {}}
# del(labels[bestFeat]) # del 会直接修改原数据 造成 'no surfacing' is not in list 的错误
#删除根节点特征
subLabels = labels[:]
del(subLabels[bestFeat])
#获取根节点特征值下的所有制
featValues = [example[bestFeat] for example in dataSet] # 该特征下的值
uniquevals = set(featValues)
# 根据该标签下的值进行划分 递归
for value in uniquevals:
subLabels = subLabels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels, flag)
return myTree
测试C4.5算法
data = pd.read_csv("dataset1train.csv",header = None)
data = py.array(data)
data = data.tolist()
labels = ['m1','m2','m3','m4','m5','m6','m7']
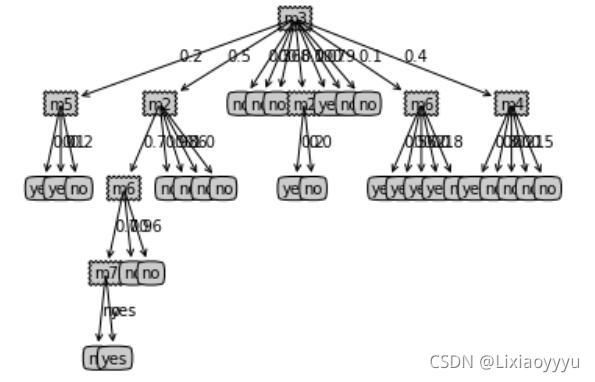
myTree2 = createTree(data,labels,'ratio')
createPlot(myTree2)
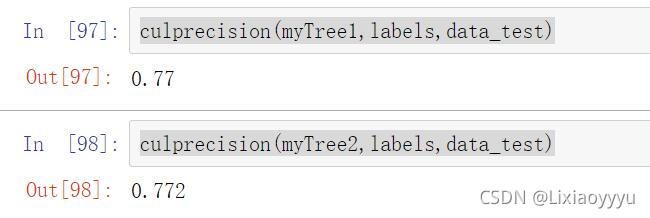
比较两个算法准确率
culprecision(myTree1,labels,data_test)
0.8117647058823529
culprecision(myTree2,labels,data_test)
0.8117647058823529
可能是由于数据集太小,而出现变化很小。
6、测试CART算法
CART算法的划分标准是最小基尼值数,先构建计算基尼指数的函数
def calcGini(dataSet):
numEntries = len (dataSet)
labelCounts = {}
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts:
labelCounts[currentLabel] = 0
labelCounts[currentLabel] +=1
Gini = 0.0
for key in labelCounts:
prob = float(labelCounts[key]) / numEntries
Gini += prob * log(prob,2)
Gini = 1 - Gini
return Gini
再对chooseBestFeatureToSplit(dataSet,flag)改造,使它能够处理三种算法。
def chooseBestFeatureToSplit(dataSet,flag):
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet)
bestInfoGain = 0.0
if(flag == 'gini'):
bestGini = calcGini(dataSet)
bestFeature = -1
for i in range(numFeatures):
featList = [example[i] for example in dataSet]
uniqueVals = set(featList)
newEntropy = 0.0
newGini = 0.0
if(flag == 'ratio' or flag =='gain'):
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
if(flag == 'gini'):
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newGini += prob * calcGini(subDataSet)
if(flag == 'gain'):
infoGain = baseEntropy - newEntropy
if(flag == 'ratio'):
infoGain = baseEntropy - newEntropy
if(calcfectShannonEnt(dataSet,i) == 0):
infoGain = infoGain/1
else:
infoGain = infoGain/calcfectShannonEnt(dataSet,i)
#print(infoGain)
if(flag == 'gini'):
if(newGini < bestGini):
bestGini = newGini
bestFeature = i
print(bestFeature)
print(newGini)
else: #flag == 'ratio' flag == 'gain'
if(infoGain > bestInfoGain ):
bestInfoGain = infoGain
bestFeature = i
print(bestFeature)
print(infoGain)
return bestFeature
生成对应的决策树
myTree3 = createTree(data,labels,'gini')
createPlot(myTree3)
culprecision(myTree3,labels,data_test)
#0.8117647058823529
四、总结
熵用来衡量信息的不确定性,不确定性越大,熵越大
通过选择最大信息增益、最大信息增益率作为标准对数据集进行划分,可以减小信息的不确定性
最大信息增益的缺点是:趋向于特征值多的特征
最大信息增益率的缺点是:趋向于特征值少的特征
基尼指数表示信息的纯度,信息纯度越高,基尼指数越小
通过选择最小基尼指数作为标准划分数据集可以调高数据集的纯度