联邦学习-安全树模型 SecureBoost之XGBoost
文章目录
- 1 联邦学习背景
- 2 联邦学习树模型方案
- 5 XGBoost概述
- 6 树的目标函数
-
- 6.1 加法模型
- 6.2 泰勒展开
- 7 树的生成策略
- 8 树的生成算法
- 9 参考资料
- 10 番外篇
1 联邦学习背景
鉴于数据隐私的重要性,国内外对于数据的保护意识逐步加强。2018年欧盟发布了《通用数据保护条例》(GDPR),我国国家互联网信息办公室起草的《数据安全管理办法(征求意见稿)》因此数据在安全合规的前提下自由流动,成了大势所趋。这些法律法规的出台,不同程度的对人工智能传统处理数据的方式提出更多的挑战。
AI高度发展的今天,多维度高质量的数据是制约其进一步发展的瓶颈。随着各个组织对于数据的重视程度的不断提升,跨组织以及组织内部不同部门之间的数据合作将变得越来越谨慎,造成了数据大量的以孤岛的形式存在
![]()
联邦学习的本质是基于数据隐私保护一种分布式机器学习技术或机器学习框架。它的目标是在保证数据隐私安全及合法合规的基础上,在模型无损的前提实现共同建模,提升AI模型的效果,进行业务的赋能。
那么既然是建模,在工业界最近若干年比较出名的大致可以分为GBDT和神经网络了,但是由于联邦学习的特性,需要对用户的特征与Label进行隐私安全保护,所以需要采用同态加密、秘钥分享、差分隐私等隐私计算手段保障安全。但是基于此带来了比较大的挑战,神经网络的复杂运算,指数、对数等会给建模提出非常大的难题,以目前的硬件与软件加密技术还是非常困难的,但是对于SecureBoost来说,只需要进行简单的同态运算就解决,达到和Xgboost同样的建模效果,所以本篇文章会和大家分享下联邦学习的安全树模型-Secure Boost。
BTW,目前神经网络虽然比较难做安全屏障,无法很好的做到计算性能与模型性能的Balance,但是经过笔者长期的思考,已经有了一个自己认为靠谱的方案,后续会逐步验证,如果最终验证靠谱,会和大家Share出来一起分享。
由于树模型相对来说知识较多,所以无法一步到位解决清晰SecureBoost,故本文章分成以下主题来进行,主要的脉络就是:决策树 -> 集成方法Bagging & Boosting -> GBDT -> XGBoost -> Secure Boost Tree。希望读者可以通过这一系列文章,对联邦学习的SecureBoost方法有一个整体的全方位的掌握。
其实,对于树模型系列来说,笔者以前做算法的时候,也在大量的使用,并且觉得自己是理解到位的,但是在我写联邦学习安全树模型的时候,发现很多的地方并没有理解透彻,有很多细节是没有考虑到的,写着写着就会发现自己的理论厚度不够,细节没有吃透。后来也花了大量的精力和时间去充电,这个事情也让我明白了,很多东西你看起来懂了,其实并没有懂,只有去真正的用心的去做过一遍,你才有些懂了,无论做什么事情脚踏实地才是最重要的。
2 联邦学习树模型方案
众所周知,上古时期的机器学习,受限于大数据、大算力与大框架的三座大山,传统的统计机器学习方法大方异彩,基本是LR、Xgboost的天下,LR属于线性的模型,无法充分的拟合非线性的数据分布。但是GBDT则属于非线性的模型,虽然说相对深度学习来说,他的非线性拟合能力并不是那么强大,但是也可以在有限的程度下,对非线性的分布进行形式化,从而形成核心的竞争力。在当时的情况下,也算是一个新的比特大陆,一个机器学习从业者,只要会用Xgb、理解Xgb基本都会有大把的公司欢迎加入。
在工业界搜广推的场景中,基本上都可以看到Xgboost的身影,基本可以说一个Xgb能用的明白,就可以在工业界占据一个位置。同时在Kaggle竞赛中,Xgb也是经常作为黑马出现。所以说Xgb就是一个大杀器,兵峰所致,所向披靡。即使在现在深度学习大行其道的情况下,Xgb依然活跃,在一些领域数据量不是那么巨大的情况下,Xgb依然在继续发光发热。
哲学告诉我们,万事万物都不是作为孤立的存在,都有着千变万化的联系。故针对联邦学习而言,我们既要做安全的深度网络模型,也要做安全的Xgb模型,那么在前两章介绍了《联邦学习-安全树模型 SecureBoost之Desicion Tree》和《联邦学习-安全树模型 SecureBoost之集成学习》,我们已经介绍了决策树、集成学习、Bagging、Boosting、GBDT后,基础部分基本就下Xgb了,那么本章介绍下XGBoost,后续再来一章介绍 安全的XGBoost也就是SecureBoostTree
5 XGBoost概述
XGBoost属于Ensemble Learning集成学习的范畴,属于Boosting方法,基于残差去训练模型来拟合真实数据场景,基于梯度直方图进行高效计算,实现了超大规模并行计算Boosting Tree,是目前最快最好的开源Boosting Tree框架,比常见的其他框架快10倍以上。类似的实现方式还有LightGBM、HistGradientBoostingClassifier等。
实现里面体现算法与工程深度融合的优雅方式,相对于GBDT,XGBoost有以下几方面的优化:
- GBDT将目标函数泰勒展开到一阶,而xgboost将目标函数泰勒展开到了二阶,Xgboost保留更多有关目标函数的信息
- GBDT是给新的基模型寻找新的拟合标签(前面加法模型的负梯度),而xgboost是给新的基模型寻找新的目标函数(目标函数关于新的基模型的二阶泰勒展开)
- xgboost加入了L2正则化项,有利于模型获得更低的方差。
- xgboost增加了自动处理缺失值特征的策略。通过把带缺失值样本分别划分到左子树或者右子树,比较两种方案下目标函数的优劣,从而自动对有缺失值的样本进行划分,无需对缺失特征进行填充预处理
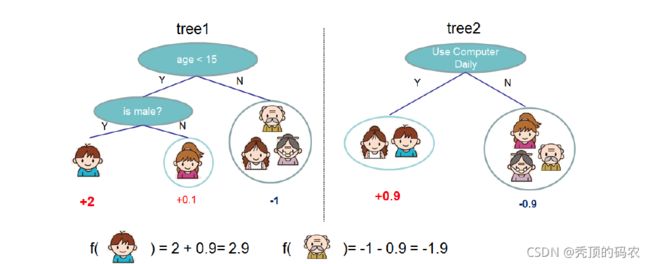
举个例子:下图中,由两棵树构成了一个boosting算法,下面和大家分享下这个例子。
- 训练样本中一共有五个,爷爷、奶奶、妈妈、儿子、女儿。
- 第一棵树里面,首先按照年龄是否小于15分成两个节点,右边结点的爷爷、奶奶、妈妈全是负类(不爱打游戏),无需再分割。左结点再按照性别分割,分为儿子和女儿,最终形成三个叶子结点,确定了三个输出值。
- 第二棵树里面,首先按照是否经常使用Computer划分为两个结点,并且因为继续分裂不再有信息增益,因此不再分裂,形成两个叶子结点。
- 推理过程:将“儿子”这个样本输入到这个由两棵树构成的boosting算法中,第一课Tree的输出值为2,那么加上第二棵tree的输出值0.9,则最后输出预测值2.9。
机器学习里面关于监督学习有个非常重要的理念,机器学习关键三部曲,模型、策略、算法。故Xgb的模型属于基模型的累加,策略是损失最小化(常见的损失函数是MSE与Logistic),算法采用分位近似计算枚举最佳分裂点。
6 树的目标函数
首先,提到目标函数,大家耳熟能详的用于分类的MSE以及用于回归的Logistics,XGB
的损失函数也可以使用这两个以及任意的支持二阶导数的损失函数,同时由于XGB使用正则化项防止过拟合,提升模型的泛化能力,所以定义XGBoost的目标函数如下:
6.1 加法模型
XGB之所以有时候难以理解,其实是有原因的。一般模型的超参只是模型的参数,但是对于拟合的Lable并不在此列,但是XGB的加法模型,通过一个个的基模型进行拟合,所以第一棵树的时候,用于拟合Lable的初始Y值也是超参,所以这点大家要注意下,当然有些神人如果第一步超参设置的神准,那么模型也就没必要训练下去了。
具体加法模型如下:
- 设置模型初始值Y的超参: y i ‘ 0 = 初 始 超 参 {y^`_i} ^{0} = 初始超参 yi‘0=初始超参
- 第一棵树: y i ‘ 1 = y i ‘ 0 + f 1 ( x ) {y^`_i} ^{1} = {y^`_i} ^{0} + f_1(x) yi‘1=yi‘0+f1(x)
- 第二棵树: y i ‘ 1 = y i ‘ 1 + f 2 ( x ) {y^`_i} ^{1} = {y^`_i} ^{1} + f_2(x) yi‘1=yi‘1+f2(x)
- …
- 第n棵树: y i ‘ 1 = y i ‘ ( n − 1 ) + f n ( x ) {y^`_i} ^{1} = {y^`_i} ^{(n-1)} + f_n(x) yi‘1=yi‘(n−1)+fn(x)
加上正则项,那么整体的目标函数为
O B J ( t ) = ∑ i = 1 n L ( y i , y i ‘ t ) + ∑ i = 1 n Ω ( f n ) + c o n s t a n t OBJ^{(t)} = \sum_{i=1}^nL(y_i, {y^`_i} ^{t}) + \sum_{i=1}^n\Omega(f_n) + constant OBJ(t)=i=1∑nL(yi,yi‘t)+i=1∑nΩ(fn)+constant
= ∑ i = 1 n L ( y i , y i ‘ ( t − 1 ) + f t ( x i ) ) + ∑ i = 1 n Ω ( f n ) + c o n s t a n t = \sum_{i=1}^nL(y_i, {y^`_i} ^{(t-1)} + f_t(x_i)) + \sum_{i=1}^n\Omega(f_n) + constant =i=1∑nL(yi,yi‘(t−1)+ft(xi))+i=1∑nΩ(fn)+constant
这个公式直接给出的时候,大家看得可能比较懵逼,我刚看到的时候也有这个感觉,感觉对,有感觉哪里不对,后来仔细的推导了一下,才彻底明白,下面听我娓娓道来。
- 唯一变量: f t ( x i ) f_t(x_i) ft(xi),其他的都是可以计算的。
- 正则项与常数项:将正则项进行分解,前t-1个正则项是常数,所以执行要t时刻的正则项。
6.2 泰勒展开
首先,我们看下泰勒展开的定义,以下内容来自维基百科
在数学中,泰勒级数(英语:Taylor series)用无限项连加式——级数来表示一个函数,这些相加的项由函数在某一点的导数求得。泰勒级数是以于1715年发表了泰勒公式的英国数学家布鲁克·泰勒(Sir Brook Taylor)来命名的。通过函数在自变量零点的导数求得的泰勒级数又叫做麦克劳林级数,以苏格兰数学家科林·麦克劳林的名字命名。
在这里插入图片描述
那么,针对上面的目标函数,我们进行泰勒展开,降低整体的运算复杂度,进行近似计算,上面已经描述过目标函数,那么我们将这个目标函数往泰勒展开公式里面套,所有的数学公式使用的时候都是一个字套,定义好关键要素,然后使用的使用使用关键要素往里面套就好。x对应于前 t-1棵树的预测值,它是唯一的变量, △ x \triangle x △x对应于第t棵树。
-
首先,定义关于目标函数的一阶与二阶偏导数,如下
g i = ∂ y ‘ ( t − 1 ) L ( y i , y i ‘ ( t − 1 ) ) , h i = ∂ 2 y ‘ ( t − 1 ) L ( y i , y i ‘ ( t − 1 ) ) , g_i=\partial {y^`}^{(t-1)}L(y_i, {y^`_i} ^{(t-1)}), h_i= {\partial }^2{y^`}^{(t-1)}L(y_i, {y^`_i} ^{(t-1)}), gi=∂y‘(t−1)L(yi,yi‘(t−1)),hi=∂2y‘(t−1)L(yi,yi‘(t−1)), -
然后,将一阶导数与二阶导数代入,那么目标函数变为如下
O b j ( t ) = ∑ i = 1 n [ g i f i ( x i ) + 1 2 h i f t 2 ( x i ) ] + ∑ i = 1 n Ω ( f n ) + c o n s t a n t Obj^{(t)}= \sum_{i=1}^n[g_if_i(x_i) + \frac 12h_if_t^2(x_i)] + \sum_{i=1}^n\Omega(f_n) + constant Obj(t)=i=1∑n[gifi(xi)+21hift2(xi)]+i=1∑nΩ(fn)+constant -
然后,去掉常量,由于函数中的常量在函数最小化的过程中不起作用,所以可以直接去掉
O b j ( t ) = ∑ i = 1 n [ g i f i ( x i ) + 1 2 h i f t 2 ( x i ) ] + ∑ i = 1 n Ω ( f n ) Obj^{(t)}= \sum_{i=1}^n[g_if_i(x_i) + \frac 12h_if_t^2(x_i)] + \sum_{i=1}^n\Omega(f_n) Obj(t)=i=1∑n[gifi(xi)+21hift2(xi)]+i=1∑nΩ(fn) -
然后,接着进行变量替换,用叶子节点的值进行替换变量 f t f_t ft,注意变量是叶子节点

-
求最值,因为一元二次函数最小值处,一阶导数等于零,套用一元二次函数的最值公式,我们可以轻易求出,每个叶子结点的权重 wj* 及其此时达到最优的 Obj 的目标值:

至此,完成了目标函数的推导,这个时候大家可以看到,由于进行了泰勒近似展开,目标函数由实际Lable值与t-1时刻的预测值的一阶与二阶导组成,亦损失函数的一阶与二阶导数。
7 树的生成策略
树的生成策略,整体来说还是比较简单的,对树中的每个叶子结点尝试进行分裂;每次分裂后,原来的一个叶子结点继续分裂为左右两个子叶子结点,原叶子结点中的样本集将根据该结点的判断规则分散到左右两个叶子结点中;新分裂一个结点后,我们需要检测这次分裂是否会给损失函数带来增益,增益的定义如下:
![]()
但是,数据集的样本特征维度非常大,虽然我们目前已经有明确的策略,但是一一枚举进行计算实在是个灾难,算力很难匹配,这个时候我们需要采用什么样的算法呢,请看下一节。
8 树的生成算法
在实际训练过程中,当建立第 t 棵树时,XGBoost采用贪心法进行树结点的分裂:在分裂一个结点时,我们会有很多个候选分割点,寻找最佳分割点的大致步骤如下:
- 首先,遍历每个结点的每个特征的所有可能取值;
- 然后,对每个特征,按特征值大小将特征值排序,进行候选;
- 然后,线性顺寻扫描,找出每个特征的最佳分裂特征值,作为候选;
- 最后,在所有特征的最佳分裂点中,再找出最好的分裂点(分裂后增益最大的特征及取值)

上面是一种贪心的方法,每次分裂都要遍历一遍全部的候选分裂点,做全局扫描。但当数据量过大、数据分布非常分散的情况下,贪心算法的效率就会变得极低,基本不可用。
基于此,XGBoost提出了一系列加快寻找最佳分裂点的方案,基于加权分位数略图 Weighted Quantile Sketch算法:
- 特征Pre排序+Cache:在训练之前,XGBoost会预先对每个特征按照特征值大小进行排序,然后就保存为quantile sketch内存结构,后面会重复地使用这个内存数据结构,减少冗余运算。
- 分位点法(直方图):对每个特征按照特征值排序后,采用分位点法(直方图)选取的方式,仅仅选出有限个特征作为该特征的代表分裂点,进行切分尝试最优。
- 并行查找:注意树与树之间还是串行,知识特征并行。基于各个特性已预先存储为block结构,XGBoost利用多个线程的线程池模式,进行并行地计算每个特征的最佳分割点,这不仅大大提升了结点的分裂速度,也极利于大规模训练集的适应性扩展,同时更好的支撑分布式架构。

9 参考资料
- SecureBoost: A Lossless Federated Learning Framework:https://arxiv.org/pdf/1901.08755.pdf
- XGBoost: A Scalable Tree Boosting System:https://arxiv.org/pdf/1603.02754.pdf
10 番外篇
个人介绍:杜宝坤,隐私计算行业从业者,从0到1带领团队构建了京东的联邦学习解决方案9N-FL,同时主导了联邦学习框架与联邦开门红业务。
框架层面:实现了电商营销领域支持超大规模的工业化联邦学习解决方案,支持超大规模样本PSI隐私对齐、安全的树模型与神经网络模型等众多模型支持。
业务层面:实现了业务侧的开门红业务落地,开创了新的业务增长点,产生了显著的业务经济效益。
个人比较喜欢学习新东西,乐于钻研技术。基于从全链路思考与决策技术规划的考量,研究的领域比较多,从工程架构、大数据到机器学习算法与算法框架均有涉及。欢迎喜欢技术的同学和我交流,邮箱:[email protected]