学习笔记:MATLAB优化算法应用之粒子群算法(一)
相关资源链接:
https://download.csdn.net/download/julengdong2179/12436162
一、粒子群算法简述
粒子群算法(Particle Swarm Optimization, PSO)是一种基于群体的随机优化技术,其基本思想是受鸟类群体行为的研究结果的启发。PSO算法通过模拟群体行为,将每个可能产生的解表述为群中的一个微粒,每个微粒都具有自己的位置向量和速度向量,以及一个由目标函数决定的适应度。所有微粒在搜索空间中以一定速度飞行,通过追随当前搜索到的最优值来寻找全局最优值。
粒子群算法对个体进行操作的3 条基本规则是:
①飞离最近的个体,以避免碰撞;
②飞向目标;
③飞向群体的中心。
二、PSO算法的数学模型
设在一个S维的目标搜索空间中,有 m m m个粒子组成一个群体,其中第 i i i个粒子表示为一个S维的向量 x i ⃗ = x i 1 , x i 2 , … , x i S \vec{x_i}=x_{i1},x_{i2},\ldots,x_{iS} xi=xi1,xi2,…,xiS, i = 1 , 2 , … , m i=1,2,\ldots,m i=1,2,…,m,每个粒子的位置就是一个潜在的解。将 x i ⃗ \vec{x_i} xi代入一个目标函数就可以算出其适应值,根据适应值的大小衡量解的优劣。第 i i i个粒子的飞翔的速度是S维向量,记为 V i ⃗ = V i 1 , V i 2 , … , V i S \vec{V_i}=V_{i1},V_{i2},\ldots,V_{iS} Vi=Vi1,Vi2,…,ViS。记第 i i i个粒子迄今为止搜索到的最优位置为 P i ⃗ = P i 1 , P i 2 , … , P i S \vec{P_i}=P_{i1},P_{i2},\ldots,P_{iS} Pi=Pi1,Pi2,…,PiS,整个粒子群迄今为止搜索到的最优位置为 P g ⃗ = P g 1 , P g 2 , … , P g S \vec{P_g}=P_{g1},P_{g2},\ldots,P_{gS} Pg=Pg1,Pg2,…,PgS。
假设设 f ( x ) f(x) f(x)为最小化的目标函数,则微粒i的当前最好位置由下式确定:
p i ( t + 1 ) = { p i ( t ) , if f ( x i ( t + 1 ) ) ≥ f ( x i ( t ) ) X i ( t + 1 ) , if f ( x i ( t + 1 ) ) < f ( x i ( t ) ) p_i(t+1)= \begin{cases} p_i(t), & \text {if $f(x_i(t+1))\geq f(x_i(t))$} \\ X_i(t+1), & \text{if $f(x_i(t+1))< f(x_i(t))$} \end{cases} pi(t+1)={pi(t),Xi(t+1),if f(xi(t+1))≥f(xi(t))if f(xi(t+1))<f(xi(t))并用下列公式对粒子的位置和速度进行操作:
v i ( t + 1 ) = v i ( t ) + c 1 r 1 ( t ) ( p 1 ( t ) − x i ( t ) ) + c 2 r 2 ( t ) ( p g ( t ) − x i ( t ) ) v_i(t+1)=v_i(t)+c_1r_1(t)(p_1(t)-x_i(t))+c_2r_2(t)(p_g(t)-x_i(t)) vi(t+1)=vi(t)+c1r1(t)(p1(t)−xi(t))+c2r2(t)(pg(t)−xi(t)) x i ( t + 1 ) = x i ( t ) + v i ( t + 1 ) x_i(t+1)=x_i(t)+v_i(t+1) xi(t+1)=xi(t)+vi(t+1)其中, i ∈ [ 1 , m ] i\in[1,m] i∈[1,m], m m m为粒子群的粒子个数,控制粒子群规模。 c 1 c_1 c1和 c 2 c_2 c2为学习因子, c 1 c_1 c1调节粒子飞向自身最好位置方向的步长, c 2 c_2 c2调节粒子飞向全局最好位置方向的步长。 r 1 r_1 r1和 r 2 r_2 r2为相互独立的伪随机数,服从 [ 0 , 1 ] [0,1] [0,1]上的均匀分布,用于保证粒子群移动的随机性和分散性。为了减少进化过程中粒子离开搜索空间的可能, 通常限定在一个范围之中,即 v i ∈ [ v m i n , v m a x ] v_i\in[v_{min},v_{max}] vi∈[vmin,vmax]。
根据具体问题,粒子群算法的终止条件取最大迭代次数或粒子群搜索到的最优位置满足的预定最小适应阈值。
三、PSO算法的流程
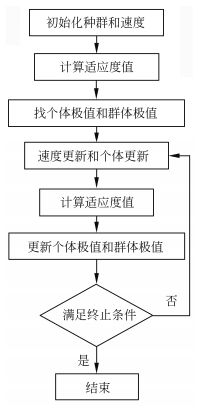
PSO 算法步骤如下:
Step1:初始化一个规模为 m 的粒子群,设定初始位置和速度,即生成一组随机解。初始化过程如下:
(1)设定群体规模 m m m。
(2)对第 i i i个粒子,在 [ v m i n , v m a x ] [v_{min},v_{max}] [vmin,vmax]内服从均匀分布产生初始位置 。
(3)对第 i i i个粒子,在 [ v m i n , v m a x ] [v_{min},v_{max}] [vmin,vmax]内服从均匀分布产生初始速度 。
Step2:计算每个粒子的适应值,即目标函数值 f ( x i ) f(x_i) f(xi)。
Step3:对每个粒子,将其适应值和其经历过的最好位置的适应值进行比较,若较好,则将其作为这个粒子当前的最好位置。
Step4:对每个粒子将其适应值和全局经历过的最好位置 p g p_g pg的适应值进行比较,若较好,则将其作为这个粒子群当前的全局最好位置。
Step5:根据公式分别对粒子的速度和位置进行更新。
Step6:如果满足终止条件,则输出解;否则返回到 Step2。
四、PSO算法的案例
对于以下非线性函数,在一定范围内找出最小值。
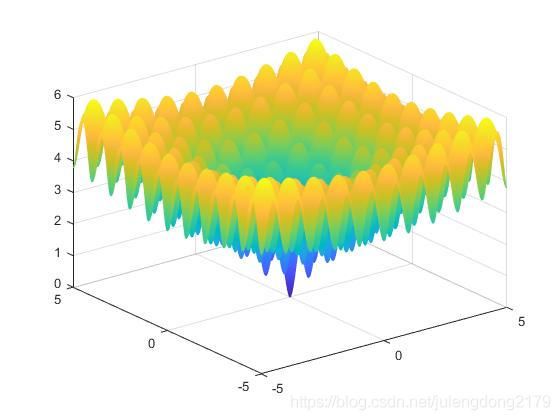
f ( x 1 , x 2 ) = − 5 e − 0.2 x 1 2 + x 2 2 − e c o s 2 π x 1 + c o s 2 π x 2 2 + 5 + e f(x_1,x_2)=-5e^{-0.2\sqrt{x_1^2+x_2^2}}-e^{\frac{cos2\pi x_1+cos2\pi x_2}{2}}+5+e f(x1,x2)=−5e−0.2x12+x22−e2cos2πx1+cos2πx2+5+e这是一个无约束优化问题,全局最优解为 f ( 0 , 0 ) = 0 f(0,0)=0 f(0,0)=0。对于这个函数,先用MATLAB程序将其图像绘制出来。
clc
clear
close all
x1=-5:0.01:5;
x2=-5:0.01:5;
for i=1:1001
for j=1:1001
z(i,j)=-5*exp(-0.2*sqrt((x1(i)^2+x2(j)^2)))-exp((cos(2*pi*x1(i))+cos(2*pi*x2(j)))/2)+exp(1)+5;
end
end
[x,y]=meshgrid(x1,x2);
mesh(x,y,z)
从函数图形中可以看出,这个函数存在很多极小值点,而最小值是 。采用粒子群算法对该函数进行最小值寻优,下面是编写MATLAB程序的过程。
1.参数初始化
% 粒子群算法中的两个参数(学习因子)
c1 = 1.5; % 粒子飞向自身最好位置方向的步长
c2 = 1.5; % 粒子飞向全局最好位置方向的步长
maxg=200; % 进化(迭代)次数
sizepop=100; % 种群规模
% 初始速度和种群个体上下边界值
Vmax=1;
Vmin=-1;
popmax=5;
popmin=-5;
2.种群初始化
for i=1:sizepop
% 随机产生一个种群
pop(i,:)=5*rands(1,2); % 初始种群
V(i,:)=rands(1,2); % 初始化速度
% 计算适应度
fitness(i)=fun(pop(i,:)); % 个体的适应度
end
% 寻找最好的个体
[bestfitness,bestindex]=min(fitness); % [最小值,最小值位置]
gbest=pop; % 个体最佳
zbest=pop(bestindex,:); % 全局最佳
fitnessgbest=fitness; % 个体最佳适应度值
fitnesszbest=bestfitness; % 全局最佳适应度值
3.迭代寻优
for i=1:maxg % maxg:迭代次数
for j=1:sizepop % sizepop:种群规模
% 速度更新
V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
V(j,V(j,:)>Vmax)=Vmax; % 控制速度上限
V(j,V(j,:)popmax)=popmax; % 控制种群上限
pop(j,pop(j,:)0.8 % rand:0-1之间的伪随机数
k=ceil(2*rand);
pop(j,k)=rand;
end
% 适应度值计算
fitness(j)=fun(pop(j,:));
%个体最优更新
if fitness(j) < fitnessgbest(j)
gbest(j,:) = pop(j,:);
fitnessgbest(j) = fitness(j);
end
%群体最优更新
if fitness(j) < fitnesszbest
zbest = pop(j,:);
fitnesszbest = fitness(j);
end
end
yy(i)=fitnesszbest;
end
4.结果分析
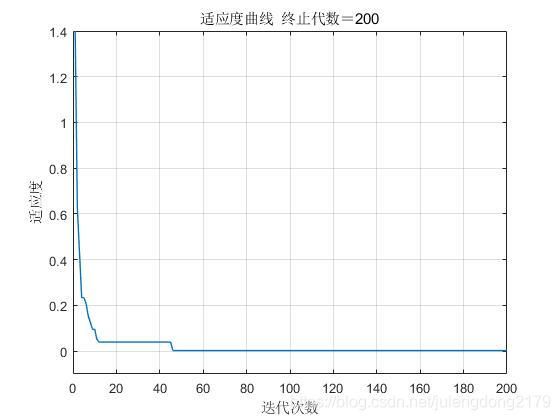
plot(yy,'Linewidth',2)
title(['适应度曲线 ' '终止代数=' num2str(maxg)]);
grid on
xlabel('迭代次数');
ylabel('适应度');
% 结果输出
zbest % 输出最佳个体值
fun(zbest) % 输出最佳适应度值
其中最优的个体值为:
zbest =
0.0024 -0.0005
从适应度曲线可看出,该函数的寻优是收敛的,最优个体值接近于理论值(0,0),因此,采用粒子群算法进行函数极值寻优,快速、准确且鲁棒性较好。
相关资源链接:
https://download.csdn.net/download/julengdong2179/12436162