详解文本生成图像的仿射变换模块(Affine Transformation)和条件批量标准化(CBN)
目录
- 一、仿射变换
- 1.1、概念
- 1.2、数学原理
- 1.3、作用方式
- 二、条件批量标准化
- 2.1、批标准化
- 2.2、条件批量标准化
- 2.3、语义条件批量标准化
- 最后
在DF-GAN、SSA-GAN、RATGAN等模型中,他们都使用到了仿射变换构建条件批量归一化或者语义条件批量归一化对图像进行约束合成。本篇文章将详细介绍什么是仿射变换,什么是条件批量归一化,其在文本生成图像领域如何从文本分布出发拟合图像分布。
一、仿射变换
1.1、概念
仿射变换又称仿射映射,其作为图像图形学领域常用的一种变换模型,主要描述一种二维坐标点对之间线性变换,可以看成线性变换和平移变换的叠加, 它保持二维图形的平直性和平行性。平直性是指图像变换后形状保持不变,平行性是指变换后图形间的相对位置保持不变。
在图形变换中,仿射变换包括放缩(尺度)、旋转、平移、剪切(偏移),变换如下所示:
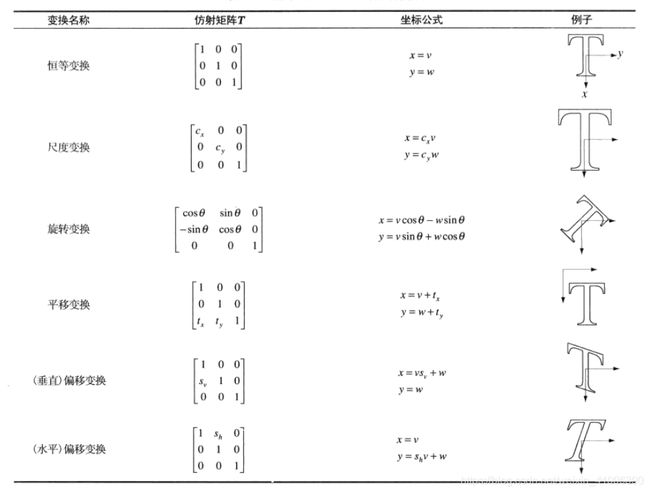
1.2、数学原理
没有平移或者平移量为0的所有仿射变换都可以叫线性变换,线性变换可以用如下变换矩阵描述: [ x ′ y ′ ] = [ a b c d ] [ x y ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right]=\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]\left[\begin{array}{l} x \\ y \end{array}\right] [x′y′]=[acbd][xy]
其中,不同变换对应的a,b,c,d约束不同,可以看上图,比如尺度变换的约束a就是α,约束d就是β,b和c为0,这样x‘=αx,y’=βy就是将图像沿着x轴放缩α倍,沿y轴放缩β倍。
而为了涵盖平移变换,我们需要给矩阵加一个维度,如下: [ x ′ y ′ 1 ] = [ a b c d e f 0 0 1 ] [ x y 1 ] \left[\begin{array}{l} x^{\prime} \\ y^{\prime} \\ 1 \end{array}\right]=\left[\begin{array}{lll} a & b & c \\ d & e & f \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right] ⎣ ⎡x′y′1⎦ ⎤=⎣ ⎡ad0be0cf1⎦ ⎤⎣ ⎡xy1⎦ ⎤ 对应的约束有:a,b,c,d,e,f,即具有6个自由度,不同基础变换的a,b,c,d,e,f约束不同。平移变换时,b=0,d=0,a=1,b=1,c=λ,f=θ,那么x‘=x+λ,y‘=y+θ,就是将图像沿x轴平移λ位,将图像沿y轴平移θ位。
为了使图像能够旋转,我们加入了三角函数
最终的矩阵变换我们定义为:
[ s cos ( θ ) − s sin ( θ ) t x s sin ( θ ) s cos ( θ ) t y 0 0 1 ] [ x y 1 ] = [ x ′ y ′ 1 ] \left[\begin{array}{ccc} s \cos (\theta) & -s \sin (\theta) & t_{x} \\ s \sin (\theta) & s \cos (\theta) & t_{y} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=\left[\begin{array}{l} x^{\prime} \\ y^{\prime} \\ 1 \end{array}\right] ⎣ ⎡scos(θ)ssin(θ)0−ssin(θ)scos(θ)0txty1⎦ ⎤⎣ ⎡xy1⎦ ⎤=⎣ ⎡x′y′1⎦ ⎤
最终的仿射变换就是线性变换和平移变换如此叠加而来的。
1.3、作用方式
仿射变换给予图片放缩、旋转、平移、偏移等几何变换功能。
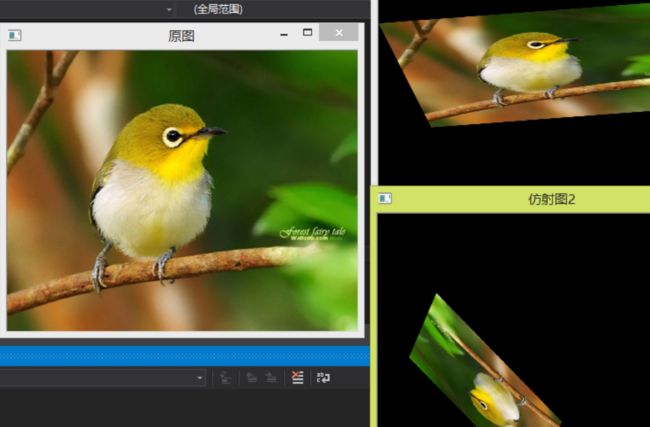
如果仿射变换作用到图像子区域或者单个像素块,则是微观的放缩、旋转、平移、偏移。
二、条件批量标准化
2.1、批标准化
批标准化(Batch Normalization,BN),又叫批量归一化,是一种用于改善人工神经网络的性能和稳定性的技术。 这是一种为神经网络中的任何层提供零均值/单位方差输入的技术。
在批标准化(BN)中,网络会求得每一个训练批次数据的均值和方差,然后使用求得的均值和方差对该批次的训练数据做归一化。由于归一化后的特征基本会被限制在正态分布下,降低了网络的表达能力,为了解决该问题,BN引入了仿射变换。仿射变换通过尺度因子γ和偏移因子β调整归一化后的数据。
数学原理如下:
x ^ n c h w = x n c h w − μ c ( x ) σ c ( x ) , μ c ( x ) = 1 N H W Σ n , h , w x n c h w , σ c ( x ) = 1 N H W Σ n , h , w ( x n c h w − μ c ) 2 + ϵ , \begin{aligned} \hat{x}_{n c h w} &=\frac{x_{n c h w}-\mu_{c}(x)}{\sigma_{c}(x)}, \\ \mu_{c}(x) &=\frac{1}{N H W} \Sigma_{n, h, w} x_{n c h w}, \\ \sigma_{c}(x) &=\sqrt{\frac{1}{N H W} \Sigma_{n, h, w}\left(x_{n c h w}-\mu_{c}\right)^{2}+\epsilon,} \end{aligned} x^nchwμc(x)σc(x)=σc(x)xnchw−μc(x),=NHW1Σn,h,wxnchw,=NHW1Σn,h,w(xnchw−μc)2+ϵ,
x ~ n c h w = γ c x ^ n c h w + β c , \tilde{x}_{n c h w}=\gamma_{c} \hat{x}_{n c h w}+\beta_{c}, x~nchw=γcx^nchw+βc,
给出图像特征 x ∈ R N × C × H × W x∈R^{N×C×H×W} x∈RN×C×H×W,首先将其归一化为每个特征通道的均值和方差,其次学习固定的变换因子γ和β,与仿射变换相似,γ尺度因子相当于仿射变换的线性变换,β偏移因子相当于仿射变换的平移变换。
2.2、条件批量标准化
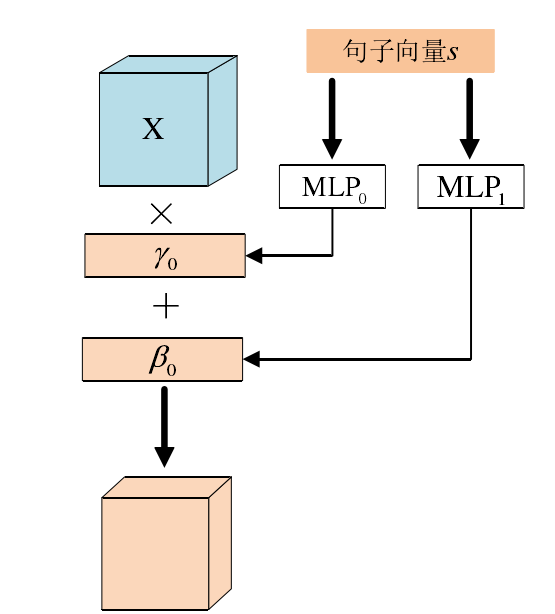
但在BN中,y和β是在反向传播过程中学习得到的可训练参数,是非条件的。因此,在一些条件图像生成任务中,条件批标准化被广泛用来替代BN,在CBN中,y和β是通过额外的神经网络学习得到的。CBN将图像底层信息和条件信息相结合,使得条件信息指导图像的特征表达。
即尺度因子γ和偏移因子β都是由条件信息得来的,在文本生成图像中,这个条件信息为文本e,而尺度因子γ和偏移因子β分别由MLP学习而来:
x ~ n c h w = γ ( con ) x ^ n c h w + β ( con ) . \tilde{x}_{n c h w}=\gamma(\text { con }) \hat{x}_{n c h w}+\beta(\text { con }) . x~nchw=γ( con )x^nchw+β( con ).
γ c = P γ ( e ˉ ) , β c = P β ( e ˉ ) \gamma_{c}=P_{\gamma}(\bar{e}), \quad \beta_{c}=P_{\beta}(\bar{e}) γc=Pγ(eˉ),βc=Pβ(eˉ)
2.3、语义条件批量标准化
如果不添加更多的空间信息,则上一步的语义感知BN将在空间上均匀地处理图像特征映射。但是在文本生成图像中,其实期望调制只对特征图中与文本相关的部分起作用,于是便有语义条件批量标准化:
x ~ n c h w = m i , ( h , w ) ( γ c ( e ˉ ) x ^ n c h w + β c ( e ˉ ) ) \tilde{x}_{n c h w}=m_{i,(h, w)}\left(\gamma_{c}(\bar{e}) \hat{x}_{n c h w}+\beta_{c}(\bar{e})\right) x~nchw=mi,(h,w)(γc(eˉ)x^nchw+βc(eˉ))
其中m不仅决定在何处添加文本信息,而且还作为权重来决定需要在图像特征图上增强多少文本信息。
![]()
部分参考于:https://blog.csdn.net/weixin_41006390/article/details/108029877
最后
个人简介:人工智能领域研究生,目前主攻文本生成图像(text to image)方向
关注我:中杯可乐多加冰
限时免费订阅:文本生成图像T2I专栏
支持我:点赞+收藏⭐️+留言
如果这篇文章帮助到你很多,希望能点击下方打赏我一杯可乐!多加冰哦