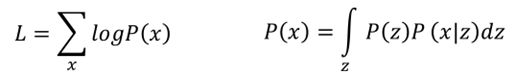【机器学习基础】无监督学习（5）——生成模型

优质资源分享

学习路线指引（点击解锁）	知识定位	人群定位
Python实战微信订餐小程序	进阶级	本课程是python flask+微信小程序的完美结合，从项目搭建到腾讯云部署上线，打造一个全栈订餐系统。
Python量化交易实战	入门级	手把手带你打造一个易扩展、更安全、效率更高的量化交易系统

前面无监督学习主要针对的是一种“降维”的学习任务，将数据降维到另一个能够表达数据含义的某种空间中，本节主要是无监督学习中的另一个任务——生成进行介绍。

---

生成模型

0.生成模型介绍

通常生成模型是指学习样本数据的分布，可以生成一些新的数据，是相对于判别模型而言的，并不特指有监督学习和无监督学习，比如朴素贝叶斯模型就是一种生成模型。

在这里生成模型主要指的是无监督学习中的生成模型，在无监督学习中的主要任务是让机器学习给定的样本，然后生成一些新的东西出来。比如：

给机器看一些图片，能够生成一些新的图片出来，给机器读一些诗，然后能够自己写诗出来。

在前面所学习的无监督学习主要是针对降维的，成为化繁为简，那么在这里的生成模型则称之为无中生有。

有三种常见的生成模型：

1、Component-by-Component

2、AutoEncoder

3、Generative Adversarial NetWork（GAN）

下面就对这三种方法进行简单的介绍，这里还是主要介绍其大致概念，后面深度学习会具体展开讨论。

1.Component-by-Component

这种方法类似于前面说的Predicted-based的方法，即根据前面的来预测后面的。比如一张3*3大小的图片：

我们希望有一个网络，输入相邻的两个像素，然后输出下一个像素。通过大量的图片来训练网络，然后给定一个初始的像素，就可以生成一张新的图片出来。

又或者通过阅读大量的文章，然后输出一张新的文章出来。

这个任务也称作Seq2Seq的学习任务，其网络主要用的就是RNN。后面到深度学习部分会对RNN再进行了解。这里先举个简单的例子：让机器自己创造一些宝可梦出来。

通过大量的宝可梦的图片训练一个网络，然后让这个网络生成一些图片出来，如图：

在测试时，首先拿一些真实的宝可梦的图片，然后盖住一部分，比如盖住50%，让机器生成这50%的图片，可以得到如右图所示的结果（并非对应关系）。

2.AutoEncoder

2.1 Review AutoEncoder

在前面说过AutoEncoder的基本概念，即通过encoder对数据的降维，而在生成模型中，decoder则可以用来生成新的数据出来。

当把AutoEncoder的网络层数增加时，就变成了deep AutoEncoder。通过给定一个code，然后输入到decoder中，就会产生新的image出来。

比如在手写识别中，数据降到2维后，给定一个二维code，则可以生成一张手写数字出来。

然而在实际中，通常对于未知的code，我们并不能保证所给的code与产生的图片属于同一个分布，这也就可能会导致当给一个code时，所生成的图片是一个“四不像”，与预期不符。

比如对于月球图片的学习，将图片降到1维（中间红色的线），然后再decode回去，如图：

假设两边的状态一个是满月一个是新月，我们想要中间找个点，得到弦月的图片，然而当我们在中间的位置任意找一个code输入到decoder进去时，并不一定能保证得到的是弦月。

也就是说我们无法真正的构造出code，我们并不知道code来自于哪个分布，因此为解决这一问题，需要变分自编码器（VAE）。

2.2 VAE简介

VAE在进行图片还原时，要保证code与decoder的输出服从一定的分布，所以V的意思代表Variational。换句话说，就是在生成code的时候我们限制这些code服从一定的分布。

VAE的直观理解是，在生成的code上加上一些“噪音”，如图：

在生成的code上面加上噪音，例如满月的图片生成code之后，在其周围加上噪音之后，那么在噪音范围内所生成的图片都是满月的图片，同理新月也是。

当我们在满月和新月的code的中间取一点时（红色的箭头），此时相当于对新月和满月进行一个加权，从而生成了弦月。

上面就是VAE的直观的解释，那么通常这个code的“噪声”是如何加呢？又为什么这么加，下面就是VAE的网络结构和原理：

可以看到code的部分变成了ci的样子，其中m是原来的code，σ是噪音分布的方差，是自己学出来的，取exp是为了保证学习的时候是一个正值，e是一个正态分布，从而得到新的code。

然而仅仅在code上加noise是不够的，在训练时，我们希望recontruction error越小越好，那么在训练时，会偏向于将σ学成0，因为当σ=0时，损失就越小。

因此在训练时要加上一项：

exp(σ)为蓝色的线，（1+σ）为红色的线，二者相减则为绿色的线，最小化这一项，则使得σi在0附近，再取exp，那么varaice则趋向于1，最后一项m的平方则可以看做是L2正则化。

因此VAE在训练时是重构误差加上上边那一项。

上边是VAE的做法和直观的理解，对于VAE的原理和推导稍微有点复杂，这里简单总结一下：

首先在高斯混合模型中，样本x的分布可以用有限个高斯分布组合而成的：

假设样本由M个混合高斯模型所组成的，x从其中一个高斯分布m而来，那么产生x的概率p(x) =p(m)*p(x|m)，总体的分布则为：

那么现在我们在训练时限制住x降维后所产生的code服从一定的标准正态分布z~N(0，I)，那么：

这里z就是降维后的code，其每一维代表一个属性，不同的是这里的高斯混合模型相当于有无限个高斯模型，因此是积分的形式。

随机出来一个z，得到z的均值和方差，就可以得到一个x，我们希望有这样一个function，输入z，输出为z的均值和方差：

这也就是decoder，同样，需要借助一个分布q(z|x)，其含义是给一个x，其在z这个空间中的分布，也就是给一个x，在z空间中的均值和方差，从而sample出一个z。其做的事刚好是跟上面的相反的。

这就是encoder。

根据所给定的样本x，根据极大似然估计：

我们需要最大化上面的式子L，接下来就是一系列的推导：

然后就变成了最大化Lower bound，进一步：

至此训练变成了最大化这两项，其中前一项可以表示为P(z)和q(z|x)的散度的负数，最大化这一项即是最小化二者的KL散度。

这一项的含义就是保证z（也就是降维的code）的分布要尽量与x在z空间中的分布保持一致。这也就限制了在降维后要保持一定的分布，那么在sample时我们可以从该分布中来生成一些样本。这也是VAE的精神所在。

而后一项就是使得z生成的x要与原来的x越接近越好，这与原来的autoencoder是一致的。

2.3 VAE的问题

VAE虽然能够比较容易地产生一些数据，但其实VAE并没有学会如何真正的去生成一些新的事物，而是一直在模仿，希望尽可能地接近已知样本。比如：

对于生成的两张图片“7”，第一张显然对于我们来说是可以接受的，而第二种是不可接受的，然而对于VAE来说，二者具有相同的损失（重构误差）。同时通过实验可以看出，VAE生成的图片一般比较“糊”，这是因为autoencoder在生成图片时，每一个pixel是独立的，它并没有考虑相互之间的关系（大局观）。

这时就需要另一个生成模型登场了——GAN。

2.4 VAE的实现

在介绍GAN之前，先来做个VAE的demo，前面简单对autoencoder进行了简单的实现，这里顺便就做一下VAE，代码没有封装，只是VAE的实现过程，便于理解本部分内容，以手写数字识别为例。

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data


# 读取数据
mnist = input_data.read_data_sets('/MNIST\_data', one_hot=True)

# 输入占位符，因为是无监督学习，所以只需要x
x = tf.placeholder(tf.float32, [None, 784])


# 定义变量从输入层到隐藏层的w,b，隐藏层假设有100个节点
encode_w = tf.Variable(tf.truncated_normal([784, 100], stddev=0.01))
encode_b = tf.Variable(tf.zeros([100]))

# 定义隐藏层到输出m那一层的权重w，假设降维到128维
encode_mean_w = tf.Variable(tf.truncated_normal([100, 128], stddev=0.01))
# 定义隐藏层到输出的variance的权重
encode_var_w = tf.Variable(tf.truncated_normal([100, 128], stddev=0.01))

# code到输出层的w和b
decode_w = tf.Variable(tf.truncated_normal([128, 784], stddev=0.01))
decode_b = tf.Variable(tf.zeros([784]))

# 隐藏层输出
encode_output = tf.nn.relu(tf.matmul(x, encode_w) + encode_b)
# 求解mean和variance
encode_mean = tf.matmul(encode_output, encode_mean_w)
encode_var = tf.matmul(encode_output, encode_var_w)
# 加上一个random normal
E = tf.random_normal([1, 128])
# 降维后的数据 m + exp(var) * E
code = tf.add(tf.exp(encode_var)*E, encode_mean)

# decoder,把code解回原数据784维
decode_output = tf.nn.relu(tf.matmul(code, decode_w) + decode_b)


# loss，原来的重构误差
decode_loss = tf.reduce_mean((decode_output - x) ** 2)
# 加上另一项误差
encode_loss = tf.reduce_mean(tf.exp(encode_var) - (1 + encode_var) + encode_mean ** 2)

loss = tf.add(decode_loss, encode_loss)

optimizer = tf.train.AdamOptimizer(learning_rate=0.001).minimize(loss)


# tf.reset\_default\_graph()

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for epoch in range(10000):
        # total\_num = int(mnist.train.num\_examples/100)
        # for i in range(total\_num):
        xs, ys = mnist.train.next_batch(100)
        _, loss_ = sess.run([optimizer, loss], feed_dict={x: xs})


        if epoch % 100 == 0:
            print('epoch:', epoch, 'loss:', loss_)

            # test
            I_test = tf.truncated_normal(shape=[1, 128], stddev=0.00001)

            decode_output_test = tf.nn.relu(tf.matmul(I_test, decode_w) + decode_b)

            decode_output_test_data = sess.run([decode_output_test])

            test_img = np.reshape(decode_output_test_data, [28, 28])

            plt.imshow(test_img, cmap='gray')

            plt.pause(0.1)折叠 

可以看到随着训练的次数增加，生成的图片也越来越“清晰”，隐约可以看到“9”的形状，一方面是因为没有对模型中的参数进行调节，加上模型较为简单，特征提取不完整。另一方面也是前面说的VAE本身的问题。

接下来结合CNN，经过卷积之后再对图片进行降维，利用VAE进行降维和还原：

# 这里首先定义一个max\_pool函数，返回的经过max\_pool之后的图片和所对应的索引
def max\_pool\_with\_argmax(net, stride):
    _, mask = tf.nn.max_pool_with_argmax(net, ksize=[1, stride, stride, 1], strides=[1, stride, stride, 1], padding='SAME')
    mask = tf.stop_gradient(mask)
    net = tf.nn.max_pool(net, ksize=[1, stride, stride, 1], strides=[1, stride, stride, 1], padding='SAME')
    return net, mask

# 根据max\_pool的索引进行反池化的操作，原理在前面CNN部分已经说过
def unpool(net, mask, stride):
    ksize = [1, stride, stride, 1]
    input_shape = net.get_shape().as_list()

    output_shape = (input_shape[0], input_shape[1] * ksize[1], input_shape[2] * ksize[2], input_shape[3])

    one_like_mask = tf.ones_like(mask)
    batch_range = tf.reshape(tf.range(output_shape[0], dtype=tf.int64), shape=[input_shape[0], 1, 1, 1])
    b = one_like_mask * batch_range
    y = mask // (output_shape[2] * output_shape[3])
    x = mask % (output_shape[2] * output_shape[3]) // output_shape[3]
    feature_range = tf.range(output_shape[3], dtype=tf.int64)
    f = one_like_mask * feature_range

    updates_size = tf.size(net)
    indices = tf.transpose(tf.reshape(tf.stack([b, y, x, f]), [4, updates_size]))
    values = tf.reshape(net, [updates_size])
    ret = tf.scatter_nd(indices, values, output_shape)
    return ret


x = tf.placeholder(tf.float32, [100, 28, 28, 1])

w_conv1 = tf.Variable(tf.truncated_normal([3, 3, 1, 64], stddev=0.01))
b_conv1 = tf.constant(0.1, shape=[64])

conv1 = tf.nn.relu(tf.nn.conv2d(x, w_conv1, strides=[1, 1, 1, 1], padding='SAME') + b_conv1)
pool1, mask1 = max_pool_with_argmax(conv1, 2)


w_conv2 = tf.Variable(tf.truncated_normal([3, 3, 64, 10], stddev=0.01))
b_conv2 = tf.constant(0.1, shape=[10])

conv2 = tf.nn.relu(tf.nn.conv2d(pool1, w_conv2, strides=[1, 1, 1, 1], padding='SAME') + b_conv2)
pool2, mask2 = max_pool_with_argmax(conv2, 2)
# pool2 = tf.nn.max\_pool2d(conv2, ksize=[1, 3, 3, 1], strides=[1, 3, 3, 1], padding='SAME')

conv_out = tf.reshape(pool2, [-1, 490])

encode_w = tf.Variable(tf.truncated_normal([490, 100]))
encode_b = tf.Variable(tf.constant(0.1, shape=[100]))

encode_output = tf.add(tf.matmul(conv_out, encode_w), encode_b)

encode_mean_w = tf.Variable(tf.truncated_normal([100, 128], stddev=0.01))
encode_var_w = tf.Variable(tf.truncated_normal([100, 128], stddev=0.01))

encode_mean = tf.matmul(encode_output, encode_mean_w)
encode_var = tf.matmul(encode_output, encode_var_w)

E = tf.random_normal([1, 128])

code = tf.add(tf.exp(encode_var) * E, encode_mean)

# decoder

decode_w = tf.Variable(tf.truncated_normal([128, 490], stddev=0.01))
decode_b = tf.Variable(tf.constant(0.1, shape=[490]))

decode_output = tf.nn.relu(tf.add(tf.matmul(code, decode_w), decode_b))

decode_output = tf.reshape(decode_output, [-1, 7, 7, 10])

t_conv2 = unpool(decode_output, mask2, 2)
t_pool1 = tf.nn.conv2d_transpose(t_conv2 - b_conv2, w_conv2, pool1.shape, [1, 1, 1, 1])

t_conv1 = unpool(t_pool1, mask1, 2)
pre_output = tf.nn.conv2d_transpose(t_conv1-b_conv1, w_conv1, x.shape, [1, 1, 1, 1])


decode_loss = tf.reduce_mean((pre_output - x) ** 2)

encode_loss = tf.reduce_mean(tf.exp(encode_var) - (1 + encode_var) + encode_mean ** 2)

loss = tf.add(decode_loss, encode_loss)

optimizer = tf.train.AdamOptimizer(learning_rate=0.001).minimize(loss)


with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for epoch in range(10000):
        # total\_num = int(mnist.train.num\_examples/100)
        # for i in range(total\_num):
        xs, ys = mnist.train.next_batch(100)
        xs = np.reshape(xs, [-1, 28, 28, 1])
        _, loss_ = sess.run([optimizer, loss], feed_dict={x: xs})


        if epoch % 100 == 0:
            print('epoch:', epoch, 'loss:', loss_)

            # test
            # 这里就有一个问题，在随机给定一个code时，在进行反池化操作时mask的选择不能用原来的训练的mask了。
            I_test = tf.truncated_normal(shape=[1, 128], stddev=0.01)

            decode_output_test = tf.nn.relu(tf.add(tf.matmul(I_test, decode_w), decode_b))

            decode_output_test = tf.reshape(decode_output_test, [-1, 7, 7, 10])

            mask2_test = tf.reshape(mask2[0], [-1, 7, 7, 10])

            t_conv2_test = unpool(decode_output_test, mask2_test, 2)
            t_pool1_test = tf.nn.conv2d_transpose(t_conv2_test - b_conv2, w_conv2, [1, 14, 14, 64], [1, 1, 1, 1])

            mask1_test = tf.reshape(mask1[0], [-1, 14, 14, 64])

            t_conv1_test = unpool(t_pool1_test, mask1_test, 2)

            pre_output_test = tf.nn.conv2d_transpose(t_conv1_test - b_conv1, w_conv1, [1, 28, 28, 1], [1, 1, 1, 1])

            decode_output_test_data = sess.run([pre_output_test], feed_dict={x: xs})

            test_img = np.reshape(decode_output_test_data, [28, 28])

            plt.imshow(test_img, cmap='gray')

            plt.pause(0.1)折叠 

可以看出上面生成的一些图片相比于之前的VAE更加清晰了，也比较像数字了，但其中有个问题就是代码中注释的那样，有的一般只做卷积，不做池化，关于池化后再test时如何生成，下去再思考。

3. GAN简介

Genrative Advesarial Networl(GAN)是机器学习中一个耳熟能详的算法，随着时间的发展，GAN也从原始的算法进化了更多的版本，这里就先对GAN进行简要的介绍，后面会单独开一节来介绍GAN及其变种算法。

GAN全名叫做生成对抗网络，顾名思义，就是在不断地生成和对抗中进行成长学习。举一个例子：

图中是枯叶蝶，其天敌是一种鸟类，在最开始时，枯叶蝶可能就是普通的蝴蝶，而这种鸟靠捕食蝴蝶为食，这种鸟认为蝴蝶不是棕色的，因此，蝴蝶进化成棕色的骗过第一代的鸟，而鸟类也在进化，进化成第二代，可以辨别蝴蝶是没有叶脉的，因此蝴蝶进一步进化成枯叶蝶。这其实就是一种对抗生成。

那么在实际的机器学中，对抗生成网络有两个部分组成，一个是Generator，另一个是Discriminator，二者在不断进行生成与对抗，称为亦师亦友的关系。在图片生成中：

第一代的Generator所及生成一些图片，给到第一代的Discriminator识别，其认为都是假的图片，

然后Generator进化到第二代，此时第二代所产生的的图片能够骗过第一代的Discriminator，单后Discriminator进化到第二代，发现第二代Generator产生的也是假的，

如此反复不断进化和迭代，直到Discriminator无法分辨Generator所产生的图片是假的。

上面是GAN的基本概念，对于GAN的原理可以解释如下：

对于实际的样本图片的数据分布我们用Pdata(x)来表示，假设它的分布是下面这样的：

在蓝色的区域是实际的图片，区域以外则产生的图片不像是真的图片，那么我们想要通过训练得到Pdata(x)的分布，假设Generator所产生的分布为PG(x)：

我们训练时希望G所产生的图片的分布于原来的图片的数据分布越接近越好。然而在实际中，我们其实并不知道PG(x)长什么样，因此这样也变得困难。

但是在GAN中，Discriminator则可以为解决这一问题提供方法，具体做法如下：

首先Generator产生一下图片数据，同时从样本中sample出一些数据

然后把这些数据Generator所产生的图片标记为0，从原数据中产生的图片标记为1，然后训练Discriminator：

那么Discriminator最终训练完成的loss则与PG(x)和Pdata(x)的JS divergence有关，也就说loss可以用来衡量两个分布有多相似。

然后Generator则可以根据这个loss进行进化成为第二代Generator。那么参数是如何更新的呢？下面举个例子：

训练完成Discriminator后，随机sample一个数据，丢进Generator中，然后产生一张图片，图片经过Discriminator，假设此时Discriminator给的分数是0.13，那么此时Generator开始调整参数（注意此时Discriminator的参数是固定不变的），使得所产生的图片丢给Discriminator让其输出值为1，然后完成进化成为Generator V2。

以上就是GAN的基本思想以及其算法的较为通俗的解释。下面给出文献中GAN的算法：

“”"

Generator：G，Discriminator:  D

• • Initialize G θg, D θd(初始化Generator和Discriminator的参数)
    • for each training
      • sample m examples{x1, x2, …,xm} from datanse;(从样本集中sample出一些数据)
      • sample m noise samples {z1, z2, …,zm} from a distribution;(从一种分布中sample出一些数据)
      • Obtaining generated data  {x’1,x’2,…x’m},x’i=G(zi);（然后把z丢进G中产生一些图片）
      • Fix G, update θd to maximize ， （固定住Generator的参数，调整Discriminator的参数，这里并不一定使用这种方法更新，还有其他方法也就衍生了其他算法）

• • • sample m noise samples{z1,z2,…,zm} from a distribution;(再另外从某种分布中sample出一些数据)
      • Fix D, update to maximize；（固定住Discriminator，调整Generator的参数，使得sample出来的那些数据让Discriminator的分数越高越好）

“”"

以上就是GAN的基本概念和算法，这里就暂时对这部分内容介绍到这里，后边会单独开一节GAN有关其他的衍生算法及其实现。

4 总结

至此有关无监督学习的内容到这里就基本完结了，总结一些，无监督学习可以概况为两种“化繁为简”和“无中生有”两类，所谓化繁为简就是数据的降维，将数据从高维空间映射到另一个空间，又能保持原数据的特征，主要方法有PCA、LLE、TSNE、AutoEncoder，无中生有主要是生成模型，主要方法有Seq2Seq、AutoEncoder、VAE、GAN。

---

后面有关机器学习的概念和内容快完结了，后面还有一些前面的提到没有补充的，后面会再进行补充。