LeetCode刷题day49

今日刷题重点—贪心

---

55. 跳跃游戏

题目描述

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

思路分析

刚看到本题一开始可能想：当前位置元素如果是3，我究竟是跳一步呢，还是两步呢，还是三步呢，究竟跳几步才是最优呢？

其实跳几步无所谓，关键在于可跳的覆盖范围！

这个范围内，别管是怎么跳的，反正一定可以跳过来。

那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点！

每次移动取最大跳跃步数（得到最大的覆盖范围），每移动一个单位，就更新最大覆盖范围。

贪心算法局部最优解：每次取最大跳跃步数（取最大覆盖范围），整体最优解：最后得到整体最大覆盖范围，看是否能到终点。

局部最优推出全局最优，找不出反例，试试贪心！

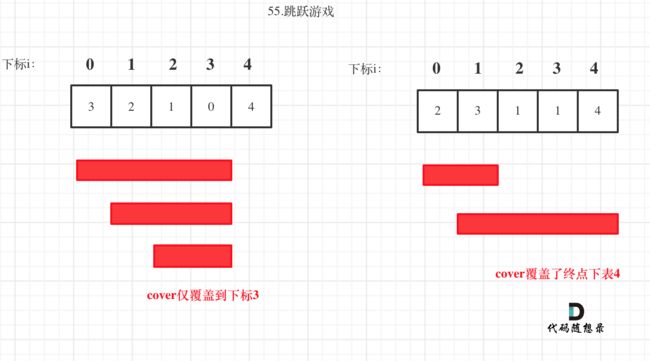
如图：

i每次移动只能在cover的范围内移动，每移动一个元素，cover得到该元素新的覆盖范围的补充，让i继续移动下去。

而cover每次只取 max(该元素数值补充后的范围, cover本身范围)。

如果cover大于等于了终点下标，直接return true就可以了。

参考代码

#include
using namespace std;

bool canJump(vector<int>& nums) { 
	int cover = 0;//最远到达(覆盖)的位置
	if(nums.size()==1) { //只有一个元素则直接结束.
		return true;
	}
	for(int i = 0; i <= cover; i++) {//范围是0-cover,每次跳跃是在cover范围内的 
		cover = max(nums[i]+i,cover);//求个最大值
		if(cover>=nums.size()-1) {//结束
			return true;
		}
	}
	return false;//如果元素遍历完毕cover还没到达最后一个元素下标,则不可能到达.
}

45. 跳跃游戏 II

题目描述

给你一个非负整数数组 nums ，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

假设你总是可以到达数组的最后一个位置。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

思路分析

本题要计算最小步数，那么就要想清楚什么时候步数才一定要加一呢？

贪心的思路，局部最优：当前可移动距离尽可能多走，如果还没到终点，步数再加一。整体最优：一步尽可能多走，从而达到最小步数。

思路虽然是这样，但在写代码的时候还不能真的就能跳多远跳远，那样就不知道下一步最远能跳到哪里了。

所以真正解题的时候，要从覆盖范围出发，不管怎么跳，覆盖范围内一定是可以跳到的，以最小的步数增加覆盖范围.覆盖范围一旦覆盖了终点，得到的就是最小步数！

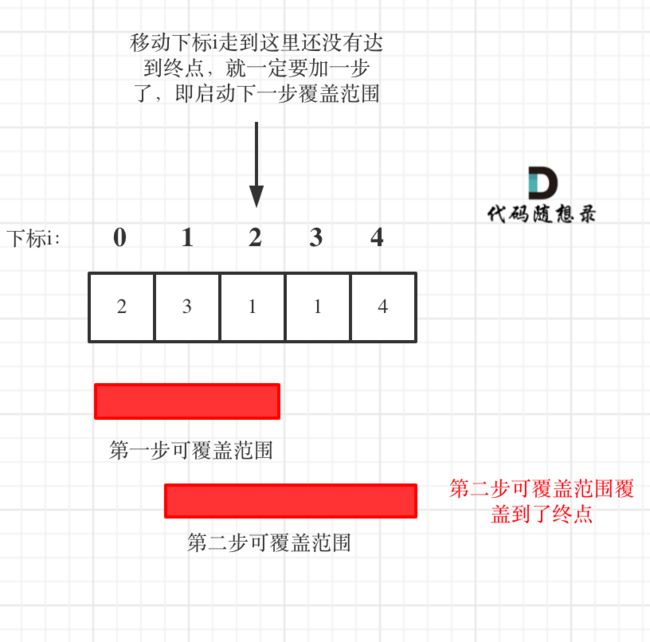
这里需要统计两个覆盖范围，当前这一步的最大覆盖和下一步最大覆盖。

如果移动下标达到了当前这一步的最大覆盖最远距离了，还没有到终点的话，那么就必须再走一步来增加覆盖范围，直到覆盖范围覆盖了终点。

如图：

参考代码

#include
using namespace std;

int jump(vector<int>& nums) {
	if(nums.size()==1){
		return 0;
	}
	int curDistance = 0;//当前最远 覆盖的下标
	int nextDistance = 0;//下一步最远覆盖的下标
	int ans = 0;//走的步数
	for(int i = 0;i < nums.size(); i++){
		nextDistance = max(nums[i]+i,nextDistance);//更新nextDistance  (在走当前这一步的时候) 
		if(i==curDistance){//相等时,说明可能需要再往前走一步了. 
			if(i!=nums.size()-1){//还没到达,则一定需要继续走 
				ans++; 
				curDistance = nextDistance;//更新覆盖范围
				if(curDistance >= nums.size()-1) {//如果新走的这一步可以到达终点,则直接结束循环 
					break;//这三行if代码,算是优化吧,不写只是在走到这个点会进行判断.
				}
			}else{//如果相等,则不用往前走了. 
				break;
			} 
		}
	} 
	return ans; 
}

1005. K 次取反后最大化的数组和

题目描述

给你一个整数数组 nums 和一个整数 k ，按以下方法修改该数组：

• 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。

重复这个过程恰好 k 次。可以多次选择同一个下标 i 。

以这种方式修改数组后，返回数组 可能的最大和 。

示例 1：

输入：nums = [4,2,3], k = 1
输出：5
解释：选择下标 1 ，nums 变为 [4,-2,3] 。

示例 2：

输入：nums = [3,-1,0,2], k = 3
输出：6
解释：选择下标 (1, 2, 2) ，nums 变为 [3,1,0,2] 。

示例 3：

输入：nums = [2,-3,-1,5,-4], k = 2
输出：13
解释：选择下标 (1, 4) ，nums 变为 [2,3,-1,5,4] 。

思路分析

贪心的思路，局部最优：让绝对值大的负数变为正数，当前数值达到最大，整体最优：整个数组和达到最大。

那么如果将负数都转变为正数了，K依然大于0，此时的问题是一个有序正整数序列，如何转变K次正负，让 数组和 达到最大。

那么又是一个贪心：局部最优：只找数值最小的正整数进行反转，当前数值可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比 反转5得到的-5 大多了），全局最优：整个 数组和 达到最大。

那么本题的解题步骤为：

• 第一步：将数组按照绝对值大小从大到小排序，注意要按照绝对值的大小
• 第二步：从前向后遍历，遇到负数将其变为正数，同时K–
• 第三步：如果K还大于0，那么反复转变数值最小的元素，将K用完
• 第四步：求和

参考代码

#include
using namespace std;

static bool cmp(int a,int b){//按照绝对值大的排在前面 
	return abs(a) > abs(b);
}

int largestSumAfterKNegations(vector<int>& nums, int k) {
	int ans = 0;
	sort(nums.begin(),nums.end());
	for(int i = 0; i < nums.size(); i++){
		if(nums[i] < 0 && k > 0) {
			nums[i]*=-1;
			k--;
		}
	}
	if(k % 2 == 1){ //如果k还有剩余,就选最小的数 反复*-1,直至k用完即可
		nums[nums.size()-1] *= -1;
	}
	for(int i = 0; i < nums.size(); i++){
		ans += nums[i];
	}
	return ans;
}

---

如果有收获！！！ 希望老铁们来个三连，点赞、收藏、转发。
创作不易，别忘点个赞，可以让更多的人看到这篇文章，顺便鼓励我写出更好的博客