BP神经网络(深度学习入门)
BP(Back Propagation) 算法是神经网络深度学习中最重要的算法之一,了解BP算法可以让我们更理解神经网络深度学习模型训练的本质,属于内功修行的部分。
BP(back propagation)神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念,是一种按照误差逆向传播算法训练的多层前馈神经网络,是应用最广泛的神经网络模型之一 。Minsky和Papert在颇具影响力的"perceptron"
一书中指出,简单的感知器只能求解线性问题,能够求解非线性问题的网络应该具有感知层,但是对隐藏层神经元的学习规则还没有合理的理论依据。
从前面介绍的感知器学习规则来看,其权值的调整取决于期望输出与实际输出之差:
Δ w i = η ( t − y ) x i \Delta w_i=\eta (t-y)x_i Δwi=η(t−y)xi
但是对于各个隐藏层的节点来说,不存在已知的期望输出,因而该学习规则不能用于隐藏层的权值调整。
BP算法的基本思想是:学习过程由信号的正向传播和误差的反向传播两个过程组成。
正向传播时,把样本的特征从输入层进行输入,信号经过各个隐藏层的处理后,最后从输出层传出。对于网络的实际的输出与期望输出之间的误差,把误差信号从最后一层逐层反传,从而获得各个层的误差学习信号,然后再根据误差学习信号来修正各层神经元的权值。
这种信号正向传播与误差反向传播,然后各层调整权值的过程是周而复始地进行的。权值不断调整的过程,也就是网络学习训练的过程。进行此过程直到网络输出误差减小到预先设置的阈值以下,或者超过预先设置的最大训练次数。

代价函数
代价函数也称为损失函数(Loss Function 或 Cost Function)。
代价函数并没有准确的定义,一般我们可以理解为是一个人为定义的函数,我们可以利用这个函数来优化模型的参数。最简单且常见的一个代价函数是均方差(MSE)代价函数,也称为二次代价函数:
E = 1 2 N ( T − N ) 2 = 1 2 N ∑ t = 1 N ( t i − y i ) 2 E=\frac{1}{2N}(T-N)^2=\frac{1}{2N}\sum_{t=1}^{N}(t_i-y_i)^2 E=2N1(T−N)2=2N1t=1∑N(ti−yi)2
矩阵可以用大写字母来表示,这里的 T T T表示真实标签, Y Y Y表示网格输出, i i i表示第 i i i个数据。 N N N表示训练样本的个数(注意,这里的 N N N是一个大于0的整数,不是矩阵)
T − Y T-Y T−Y可以得到每个训练样本与真实标签的误差。误差的值有正有负,我们可以求平方,把所有的误差都变成正的,然后除以 2 N 2N 2N。这里的2没有特别的含义,主要是我们对均方差代价函数求导的时候,式子中的2次方的2可以跟分母中的2约掉,使得公式推导看起来更整齐简洁。除以 N N N表示求每个样本的误差平均的平均值。
公式可以用矩阵形式来表达,也可以拆分为用 ∑ \sum ∑来累加各个训练样本的真实标签与网络输出的误差的平方。
梯度下降法
在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是最小二乘法。这里就对梯度下降法做一个完整的总结。
梯度
在微积分里面,对多元函数的参数求 < ! − − S t a r t F r a g m e n t − − > ∂ < ! − − E n d F r a g m e n t − − > ∂ <!−−StartFragment−−>∂<!−−EndFragment−−>偏导数,把求得的各个参数的偏导数以向量的形式写出来,就是梯度。比如函数 f ( x , y ) f(x,y) f(x,y), 分别对x,y求偏导数,求得的梯度向量就是 ( ∂ f / ∂ x , ∂ f / ∂ y ) T (∂f/∂x, ∂f/∂y)^T (∂f/∂x,∂f/∂y)T,简称 g r a d f ( x , y ) grad f(x,y) gradf(x,y)或者 ▽ f ( x , y ) ▽f(x,y) ▽f(x,y)。对于在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)的具体梯度向量就是 ( ∂ f / ∂ x 0 , ∂ f / ∂ y 0 ) T (∂f/∂x_0, ∂f/∂y_0)^T (∂f/∂x0,∂f/∂y0)T.或者 ▽ f ( x 0 , y 0 ) ▽f(x_0,y_0) ▽f(x0,y0),如果是3个参数的向量梯度,就是 ( ∂ f / ∂ x , ∂ f / ∂ y , ∂ f / ∂ z ) T (∂f/∂x, ∂f/∂y,∂f/∂z)^T (∂f/∂x,∂f/∂y,∂f/∂z)T,以此类推。
那么这个梯度向量求出来有什么意义呢?他的意义从几何意义上讲,就是函数变化增加最快的地方。具体来说,对于函数 f ( x , y ) f(x,y) f(x,y),在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0),沿着梯度向量的方向就是 ( ∂ f / ∂ x 0 , ∂ f / ∂ y 0 ) T (∂f/∂x_0, ∂f/∂y_0)^T (∂f/∂x0,∂f/∂y0)T的方向是 f ( x , y ) f(x,y) f(x,y)增加最快的地方。或者说,沿着梯度向量的方向,更加容易找到函数的最大值。反过来说,沿着梯度向量相反的方向,也就是 − ( ∂ f / ∂ x 0 , ∂ f / ∂ y 0 ) T -(∂f/∂x_0, ∂f/∂y_0)^T −(∂f/∂x0,∂f/∂y0)T的方向,梯度减少最快,也就是更加容易找到函数的最小值。
梯度下降和梯度上升
在机器学习算法中,在最小化损失函数时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数,和模型参数值。反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了。
梯度下降法和梯度上升法是可以互相转化的。比如我们需要求解损失函数 f ( θ ) f(θ) f(θ)的最小值,这时我们需要用梯度下降法来迭代求解。但是实际上,我们可以反过来求解损失函数 − f ( θ ) -f(θ) −f(θ)的最大值,这时梯度上升法就派上用场了。
下面来详细总结下梯度下降法。
梯度下降法
首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置,由于我们不知道怎么下山,于是决定走一步算一步,也就是在每走到一个位置的时候,求解当前位置的梯度,沿着梯度的负方向,也就是当前最陡峭的位置向下走一步,然后继续求解当前位置梯度,向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去,一直走到觉得我们已经到了山脚。当然这样走下去,有可能我们不能走到山脚,而是到了某一个局部的山峰低处。
从上面的解释可以看出,梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。

在详细了解梯度下降的算法之前,我们先看看相关的一些概念。
1. 步长(Learning rate):步长决定了在梯度下降迭代的过程中,每一步沿梯度负方向前进的长度。用上面下山的例子,步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度。
2.特征(feature):指的是样本中输入部分,比如2个单特征的样本 ( x ( 0 ) , y ( 0 ) ) (x(0),y(0)) (x(0),y(0)), ( x ( 1 ) , y ( 1 ) ) (x(1),y(1)) (x(1),y(1)),则第一个样本特征为 x ( 0 ) x(0) x(0),第一个样本输出为 y ( 0 ) y(0) y(0)。
3. 假设函数(hypothesis function):在监督学习中,为了拟合输入样本,而使用的假设函数,记为 h θ ( x ) h_θ(x) hθ(x)。比如对于单个特征的m个样本 ( x ( i ) , y ( i ) ) ( i = 1 , 2 , . . . m ) (x(i),y(i))(i=1,2,...m) (x(i),y(i))(i=1,2,...m),可以采用拟合函数如下:$ h_θ(x)=θ_0+θ_1x$。
4. 损失函数(loss function):为了评估模型拟合的好坏,通常用损失函数来度量拟合的程度。损失函数极小化,意味着拟合程度最好,对应的模型参数即为最优参数。在线性回归中,损失函数通常为样本输出和假设函数的差取平方。比如对于m个样本 ( x i , y i ) ( i = 1 , 2 , . . . m ) (xi,yi)(i=1,2,...m) (xi,yi)(i=1,2,...m),采用线性回归,损失函数为:
$$
J(θ_0,θ_1)=∑_{i=1}^{m}(h_θ(x_i)−y_i)^2
$$
其中 x i x_i xi表示第 i i i个样本特征, y i y_i yi表示第 i i i个样本对应的输出, h θ ( x i ) h_θ(x_i) hθ(xi)为假设函数。
梯度下降的详细算法
- 先决条件: 确认优化模型的假设函数和损失函数。
比如对于线性回归,假设函数表示为
h θ ( x 1 , x 2 , . . . x n ) = θ 0 + θ 1 x 1 + . . . + θ n x n , h_θ(x_1,x_2,...x_n)=θ_0+θ_1x_1+...+θ_nx_n, hθ(x1,x2,...xn)=θ0+θ1x1+...+θnxn,
其中 θ i ( i = 0 , 1 , 2... n ) θ_i (i = 0,1,2... n) θi(i=0,1,2...n)为模型参数, x i ( i = 0 , 1 , 2... n ) x_i (i = 0,1,2... n) xi(i=0,1,2...n)为每个样本的 n n n个特征值。这个表示可以简化,我们增加一个特征 x 0 = 1 x_0=1 x0=1 ,这样 h θ ( x 0 , x 1 , . . . x n ) = ∑ i = 0 n θ i x i h_θ(x_0,x_1,...x_n)=∑_{i=0}^nθ_ix_i hθ(x0,x1,...xn)=i=0∑nθixi
。
同样是线性回归,对应于上面的假设函数,损失函数为:
J ( θ 0 , θ 1 . . . , θ n ) = 1 2 m ∑ j = 1 m ( h θ ( x 0 ( j ) , x 1 ( j ) , . . . x n ( j ) ) − y j ) 2 J(θ_0,θ_1...,θ_n)=\frac{1}{2m}∑_{j=1}^m(h_θ(x^{(j)}_0,x^{(j)}_1,...x^{(j)}_n)−y_j)^2 J(θ0,θ1...,θn)=2m1j=1∑m(hθ(x0(j),x1(j),...xn(j))−yj)2
- 算法相关参数初始化:主要是初始化 θ 0 , θ 1 . . . , θ n θ_0,θ_1...,θ_n θ0,θ1...,θn,算法终止距离 ε ε ε以及步长 α \alpha α。在没有任何先验知识的时候,我喜欢将所有的 θ θ θ初始化为 0 0 0, 将步长初始化为1。在调优的时候再优化。
3.算法过程:
1)确定当前位置的损失函数的梯度,对于 θ i θ_i θi,其梯度表达式如下:
∂ ∂ θ i J ( θ 0 , θ 1 . . . , θ n ) \frac{∂}{∂θ_i}J(θ_0,θ_1...,θ_n) ∂θi∂J(θ0,θ1...,θn)
2)用步长乘以损失函数的梯度,得到当前位置下降的距离,即 α ∂ ∂ θ i J ( θ 0 , θ 1 . . . , θ n ) α\frac{∂}{∂θ_i}J(θ_0,θ_1...,θ_n) α∂θi∂J(θ0,θ1...,θn)对应于前面登山例子中的某一步。
3)确定是否所有的 θ i θ_i θi,梯度下降的距离都小于 ε ε ε,如果小于 ε ε ε则算法终止,当前所有的 θ i ( i = 0 , 1 , . . . n ) θ_i(i=0,1,...n) θi(i=0,1,...n)即为最终结果。否则进入步骤4.
4)更新所有的 θ θ θ,对于 θ i θ_i θi,其更新表达式如下。更新完毕后继续转入步骤1.
θ i = θ i − α ∂ ∂ θ i J ( θ 0 , θ 1 . . . , θ n ) θ_i=θ_i−α\frac{∂}{∂θ_i}J(θ_0,θ_1...,θ_n) θi=θi−α∂θi∂J(θ0,θ1...,θn)
梯度下降的算法调优
在使用梯度下降时,需要进行调优。哪些地方需要调优呢?
-
算法的步长选择。在前面的算法描述中,我提到取步长为1,但是实际上取值取决于数据样本,可以多取一些值,从大到小,分别运行算法,看看迭代效果,如果损失函数在变小,说明取值有效,否则要增大步长。前面说了。步长太大,会导致迭代过快,甚至有可能错过最优解。步长太小,迭代速度太慢,很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较为优的值。
-
算法参数的初始值选择。 初始值不同,获得的最小值也有可能不同,因此梯度下降求得的只是局部最小值;当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险,需要多次用不同初始值运行算法,关键损失函数的最小值,选择损失函数最小化的初值。
3.归一化。由于样本不同特征的取值范围不一样,可能导致迭代很慢,为了减少特征取值的影响,可以对特征数据归一化,也就是对于每个特征 x x x,求出它的期望 x ‾ \overline{x} x 和标准差 s t d ( x ) std(x) std(x),然后转化为:
$$
\frac{x−\overline{x} }{std(x)}
$$
这样特征的新期望为0,新方差为1,迭代速度可以大大加快。
梯度下降三大方法
1.批量梯度下降法(Batch Gradient Descent)
批量梯度下降法,是梯度下降法最常用的形式,具体做法也就是在更新参数时使用所有的样本来进行更新,这个方法对应于前面的线性回归的梯度下降算法,也就是说梯度下降详细算法就是批量梯度下降法。
θ j = θ i − α ∑ j = 1 m ( h θ ( x 0 ( j ) , x 1 ( j ) , . . . x n ( j ) ) − y j ) x i ( j ) θ_j=θ_i-\alpha∑_{j=1}^m(h_θ(x^{(j)}_0,x^{(j)}_1,...x^{(j)}_n)−y_j)x^{(j)}_i θj=θi−αj=1∑m(hθ(x0(j),x1(j),...xn(j))−yj)xi(j)
由于我们有m个样本,这里求梯度的时候就用了所有m个样本的梯度数据。
2.随机梯度下降法(Stochastic Gradient Descent)
随机梯度下降法,其实和批量梯度下降法原理类似,区别在与求梯度时没有用所有的m个样本的数据,而是仅仅选取一个样本j来求梯度。对应的更新公式是:
θ j = θ i − α ( h θ ( x 0 ( j ) , x 1 ( j ) , . . . x n ( j ) ) − y j ) x i ( j ) θ_j=θ_i-\alpha(h_θ(x^{(j)}_0,x^{(j)}_1,...x^{(j)}_n)−y_j)x^{(j)}_i θj=θi−α(hθ(x0(j),x1(j),...xn(j))−yj)xi(j)
随机梯度下降法,和前面的批量梯度下降法是两个极端,一个采用所有数据来梯度下降,一个用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说,随机梯度下降法由于每次仅仅采用一个样本来迭代,训练速度很快,而批量梯度下降法在样本量很大的时候,训练速度不能让人满意。对于准确度来说,随机梯度下降法用于仅仅用一个样本决定梯度方向,导致解很有可能不是最优。对于收敛速度来说,由于随机梯度下降法一次迭代一个样本,导致迭代方向变化很大,不能很快的收敛到局部最优解。
那么,有没有一个中庸的办法能够结合两种方法的优点呢?有!这就是下面的小批量梯度下降法。
3.小批量梯度下降法(Mini-batch Gradient Descent)
小批量梯度下降法是批量梯度下降法和随机梯度下降法的折中,也就是对于 m m m个样本,我们采用 x x x个来迭代, 1 < x < m 1
θ j = θ i − α ∑ j = t t + x − 1 ( h θ ( x 0 ( j ) , x 1 ( j ) , . . . x n ( j ) ) − y j ) x i ( j ) θ_j=θ_i-\alpha∑_{j=t}^{t+x-1}(h_θ(x^{(j)}_0,x^{(j)}_1,...x^{(j)}_n)−y_j)x^{(j)}_i θj=θi−αj=t∑t+x−1(hθ(x0(j),x1(j),...xn(j))−yj)xi(j)
梯度下降算法和其他无约束算法的比较
在机器学习中的无约束优化算法,除了梯度下降以外,还有前面提到的最小二乘法,此外还有牛顿法和拟牛顿法。
梯度下降法和最小二乘法相比,梯度下降法需要选择步长,而最小二乘法不需要。梯度下降法是迭代求解,最小二乘法是计算解析解。如果样本量不算很大,且存在解析解,最小二乘法比起梯度下降法要有优势,计算速度很快。但是如果样本量很大,用最小二乘法由于需要求一个超级大的逆矩阵,这时就很难或者很慢才能求解解析解了,使用迭代的梯度下降法比较有优势。
梯度下降法和牛顿法/拟牛顿法相比,两者都是迭代求解,不过梯度下降法是梯度求解,而牛顿法/拟牛顿法是用二阶的海森矩阵的逆矩阵或伪逆矩阵求解。相对而言,使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。
Delta学习规则
Delata学习规则是一种利用梯度下降法的一般性学习规则,其实就是利用梯度下降法来最小化代价函数。
例如我们所介绍的均方差代价函数,一个样本的均方差代价函数公式定义如下:
E = 1 2 ( T − Y ) 2 = 1 2 ( t − y ) 2 = 1 2 ( t − f ( W X ) ) 2 E=\frac{1}{2}(T-Y)^2=\frac{1}{2}(t-y)^2 =\frac{1}{2}(t-f(WX))^2 E=21(T−Y)2=21(t−y)2=21(t−f(WX))2
误差 E E E是 W W W的函数,我们可以使用梯度下降法来最小化 E E E的值,权值矩阵的变化 Δ W \Delta W ΔW等于负的学习率( − η -\eta −η)乘以 E E E对 W W W求导:
Δ W = − η E ′ = η X T ( t − y ) f ′ ( W X ) = η X T δ \Delta W=-\eta {E}'=\eta X^T(t-y){f}'(WX)=\eta X^T \delta ΔW=−ηE′=ηXT(t−y)f′(WX)=ηXTδ
注意,这里的 X X X和 W W W都是矩阵,所以这里求导的时候是对矩阵 W W W进行求导,矩阵求导的方式和单元素求导的方式有一些不同。对单个w元素的权值变化计算:
Δ w i = − η E ′ = η x i ( t − y ) f ′ ( W X ) = η x i δ \Delta w_i=-\eta {E}'=\eta x_i(t-y){f}'(WX)=\eta x_i \delta Δwi=−ηE′=ηxi(t−y)f′(WX)=ηxiδ
BP神经网络模型
BP神经网络学习算法可以说是目前最成功的神经网络学习算法。显示任务中使用神经网络时,大多数是使用BP算法进行训练.
在我看来BP神经网络就是一个”万能的模型+误差修正函数“,每次根据训练得到的结果与预想结果进行误差分析,进而修改权值和阈值,一步一步得到能输出和预想结果一致的模型。举一个例子:比如某厂商生产一种产品,投放到市场之后得到了消费者的反馈,根据消费者的反馈,厂商对产品进一步升级,优化,从而生产出让消费者更满意的产品。这就是BP神经网络的核心。
下面就让我们来看看BP算法到底是什么东西。BP网络由输入层、隐藏层、输出层组成。
给定训练集 D = ( x 1 , y 1 ) , ( x 2 , y 2 ) … ( x n , y n ) D={(x_1,y_1),(x_2,y_2)…(x_n,y_n)} D=(x1,y1),(x2,y2)…(xn,yn),其中 x n ϵ R d x_nϵR^d xnϵRd, y n ϵ R l y_nϵR^l ynϵRl,表示输入示例由 d d d个属性组成,输出 l l l维实值变量。现在,我们看看如何求得输出值,以及怎么由输出值调整权值和阈值。
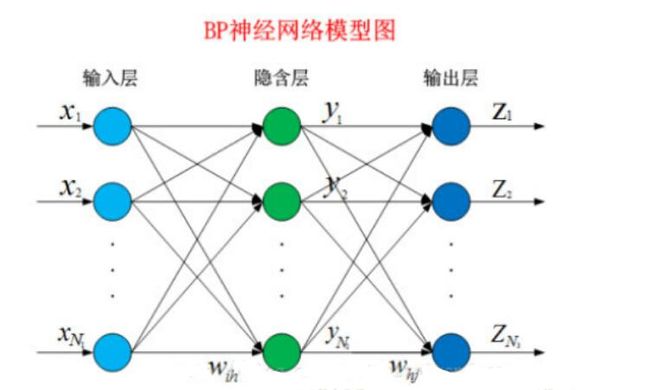
神经元是以生物研究及大脑的响应机制而建立的拓扑结构网络,模拟神经冲突的过程,多个树突的末端接受外部信号,并传输给神经元处理融合,最后通过轴突将神经传给其它神经元或者效应器。神经元的拓扑结构如图:
对于第 i i i个神经元, x 1 、 x 2 、 … 、 x j x_1、x_2、…、x_j x1、x2、…、xj为神经元的输入,输入常为对系统模型关键影响的自变量, w 1 、 w 2 、 … 、 w j w_1、w_2、…、w_j w1、w2、…、wj为连接权值调节各个输入量的占重比。将信号结合输入到神经元有多种方式,选取最便捷的线性加权求和可得 n e t i neti neti神经元净输入:
N e t i n = ∑ i = 1 n w i ∗ x i Net_{in}=\sum_{i=1}^nw_i*x_i Netin=i=1∑nwi∗xi
θ i \theta_i θi表示该神经元的阈值,根据生物学中的知识,只有当神经元接收到的信息达到阈值是才会被激活。因此,我们将 N e t i n Net_{in} Netin和 θ j \theta_j θj进行比较,然后通过激活函数处理以产生神经元的输出。
激活函数:激活函数这里我们不多重述。如果输出值有一定的范围约束,比如用来分类,一般我们用的最多的是 S i g m o d Sigmod Sigmod函数,它可以把输入从负无穷大到正无穷大的信号变换成0到1之间输出。如果没有约束的话,我们可以使用线性激活函数(即权值相乘之和)。这样我们得到的输出为:
y j = f ( N e t i n − θ j ) y_j=f(Net_{in}-\theta_j) yj=f(Netin−θj)
我们可以将公式化简一下,设第一个输入值永远为 θ \theta θ,权值为-1,则我们可以得到公式:
y j = f ( ∑ i = 0 n w i ∗ x i ) y_j=f(\sum_{i=0}^nw_i*x _i) yj=f(i=0∑nwi∗xi)
其中 w 0 = − 1 , x 0 = θ j w_0=-1,x_0= \theta_j w0=−1,x0=θj,其中 f f f为选择的激活函数。
已经知道在BP神经网络模型中,我们有三层结构,输入层、隐藏层、输出层,因此输入层到隐藏层的权值,设为 v i h v_{ih} vih,隐藏层第h个神经元的阈值我们设为 γ h \gamma_h γh。隐藏层到输出层的权值,设为 w h j w_{hj} whj,输出层第j个神经元的阈值我们用 θ j \theta_j θj表示。在下面这张图里,有 d d d输入神经元, q q q个隐藏神经元,隐藏有 q q q个隐藏神经元阈值, l l l个输出神经元,因此有 l l l个输出神经元阈值。
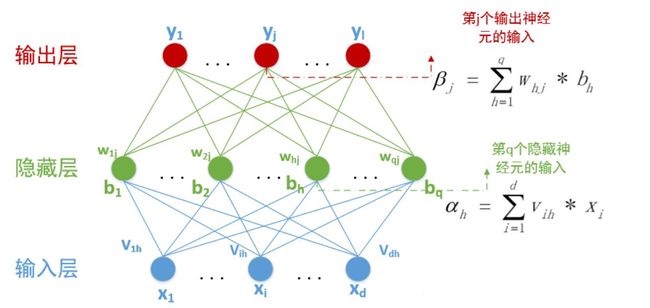
其中 β j \beta_j βj中的 b h = f ( α h − γ h ) b_h=f(\alpha_h-\gamma_h) bh=f(αh−γh)。隐藏层和输出层的激活函数,在这里我们暂时全部用 S i g m o d Sigmod Sigmod函数。
在某个训练示例 ( x k , y k ) (x_k,y_k) (xk,yk)中,假设神经网络的训练输出为 y k , = ( y 1 k , , y 2 k , , ⋯ , y l k , ) y_{k^,}=({y_1^{k^,},y_2^{k^,},\cdots,y_l^{k^,}}) yk,=(y1k,,y2k,,⋯,ylk,),输出为 l l l维向量,其中
y i k , = f ( β i − θ i ) y_i^{k^,}=f(\beta_i-\theta_i) yik,=f(βi−θi)
那么这次预测结果的误差我们可以用最小二乘法表示:
E k = 1 2 ∑ j = 1 l ( y j k , − y j k ) 2 E_k=\frac{1}{2}\sum_{j=1}^l(y_j^{k^,}-y_j^k)^2 Ek=21j=1∑l(yjk,−yjk)2
而我们现在要做的就是根据这个误差去调整 ( d + l + 1 ) q + l (d+l+1)q+l (d+l+1)q+l个参数的值,一步一步缩小 E k E_k Ek。那么从现在开始,我们就要进入数学的世界了。这里我们使用最常用的算法:梯度下降法来更新参数。函数永远是沿着梯度的方向变化最快,那么我们对每一个需要调整的参数求偏导数,如果偏导数>0,则要按照偏导数相反的方向变化;如果偏导数<0,则按照此方向变化即可。于是我们使用-1*偏导数则可以得到参数需要变化的值。同时我们设定一个学习速率 η \eta η,这个学习速率不能太快,也不能太慢。太快可能会导致越过最优解;太慢可能会降低算法的效率。(具体设多少就属于玄学调参的领域了)。因此我们可以得到一个参数调整公式:
P a r a m + = − η ∂ E k ∂ P a r a m Param+=-\eta\frac{∂E_k}{∂Param} Param+=−η∂Param∂Ek
首先我们看看隐藏层到输出层的权值调整值:
Δ w h j = − η ∂ E k ∂ w h j \Delta w_{hj}=-\eta\frac{\partial E_k}{\partial w_{hj}} Δwhj=−η∂whj∂Ek
综合我们可得:
Δ w h j = − η ∂ E k ∂ w h j = − η g i b h = − η ( y j k ′ − y j k ) ⋅ y j k ′ ⋅ ( 1 − y j k ′ ) ⋅ b h ⋯ \Delta w_{hj}=-\eta\frac{\partial E_k}{\partial w_{hj}}=-\eta g_i b_h=-\eta (y_j^{k^{'}}-y_j^k) \cdot y_j^{k^{'}}\cdot (1-y_j^{k^{'}})\cdot b_h \cdots Δwhj=−η∂whj∂Ek=−ηgibh=−η(yjk′−yjk)⋅yjk′⋅(1−yjk′)⋅bh⋯
同理:
Δ θ j = − η ∂ E k ∂ θ j = − η ∂ E k ∂ y j k ′ ⋅ ∂ y j k ′ ∂ θ j = η ⋅ g j ⋯ \Delta \theta_j=-\eta \frac{\partial E_k}{\partial \theta_j}=-\eta \frac{\partial E_k}{\partial y_j^{k^{'}}}\cdot\frac{\partial y_j^{k^{'}}}{\partial \theta_j}=\eta\cdot g_j \cdots Δθj=−η∂θj∂Ek=−η∂yjk′∂Ek⋅∂θj∂yjk′=η⋅gj⋯
我们再看看 Δ v i h \Delta v_{ih} Δvih的值怎么求,一个 v v v权值会影响所有的 β \beta β,
Δ v i h = − η e h x i ⋯ ⋯ ⋯ ⋯ \Delta v_{ih}=-\eta e_h x_i \cdots\cdots\cdots\cdots Δvih=−ηehxi⋯⋯⋯⋯
Δ γ h = η e h ⋯ ⋯ ⋯ \Delta \gamma_h=\eta e_h \cdots \cdots\ \cdots Δγh=ηeh⋯⋯ ⋯
其中
e h = ( ∑ j = 1 l ∂ E k ∂ β j ⋅ ∂ β j ∂ b j ) ⋅ f ′ ( α h − γ h ) = ( ∑ j = 1 l ( y j k , − y j k ) ⋅ f ’ ( β j − θ j ) ⋅ w h j ) ⋅ f ′ ( α h − γ h ) ⋯ ⋯ ⋯ e_h=(\sum_{j=1}^l \frac{\partial E_k}{\partial \beta_j}\cdot \frac{\partial \beta_j}{\partial b_j})\cdot f^{'}(\alpha_h-\gamma_h)=(\sum_{j=1}^l(y_j^{k^,}-y_j^k)\cdot f^{’}(\beta_j-\theta_j) \cdot w_{hj})\cdot f^{'}(\alpha_h-\gamma_h) \cdots \cdots \cdots eh=(j=1∑l∂βj∂Ek⋅∂bj∂βj)⋅f′(αh−γh)=(j=1∑l(yjk,−yjk)⋅f’(βj−θj)⋅whj)⋅f′(αh−γh)⋯⋯⋯
至此,我们所有得公式都推导完毕了,剩下做的就是设定一个迭代终止条件,可以是误差小于一定值时终止递归,也可以是设定迭代次数。这样一个BP神经网络模型就算是设计结束。
BP算法推导总结
我们最后推导得到的结论也就是权值调整的公式为:
Δ W h = η ( Y h − 1 ) T δ h \Delta W^h=\eta (Y^{h-1})^T \delta^h ΔWh=η(Yh−1)Tδh
这里的 Δ W h \Delta W^h ΔWh表示第 h h h层权值矩阵 W W W的变化, η \eta η表示学习率, Y h − 1 Y^{h-1} Yh−1表示网络第 h − 1 h-1 h−1层的输出, δ h \delta^h δh表示第 h h h层的学习信号。
η \eta η是人为设置的超参数:只要把数据传入网络中就可以计算出 Y h − 1 Y^{h-1} Yh−1网络第 h − 1 h-1 h−1层的输出,所以这里要重点关注的是第 h h h层的学习信号 δ h \delta^h δh。学习信号有两个不同的公式,输出层的学习信号公式为:
δ h + 1 = ( T − Y h + 1 ) f ′ ( Y h W h + 1 ) \delta^{h+1}=(T-Y^{h+1}){f}'(Y^hW^{h+1}) δh+1=(T−Yh+1)f′(YhWh+1)
这里的 δ h + 1 \delta^{h+1} δh+1表示输出层的学习信号; T T T表示数据的标签值; Y h + 1 Y^{h+1} Yh+1表示模型的预测值; f ′ {f}' f′表示激活函数的导数; Y h W h + 1 Y^hW^{h+1} YhWh+1表示输出层信号的汇总。
T T T是已知的数据标签; Y h + 1 Y^{h+1} Yh+1可以通过传入数据计算得到;激活函确定以后, f ′ {f}' f′也是已知的; Y h Y^h Yh可以通过传入数据计算得到; W h + 1 W^{h+1} Wh+1在网络进行随机初始化以后也确定下来了。所以这个公式里面的所有值都是已知的,或者可以通过计算得到。把 δ h + 1 \delta^{h+1} δh+1计算出来以后,代入式中就可以计算出输出层的权值矩阵要如何调整。
除输出层外,剩下的网络层的学习信号的公式都是:
δ h = δ h + 1 ( W h + 1 ) T f ′ ( Y h − 1 W h ) \delta^{h}=\delta^{h+1}(W^{h+1})^T{f}'(Y^{h-1}W^{h}) δh=δh+1(Wh+1)Tf′(Yh−1Wh)
从式中我们可以看到,第 h h h层的学习信号 δ h \delta^{h} δh跟它下一层 h + 1 h+1 h+1层的学习信号 δ h + 1 \delta^{h+1} δh+1有关系,并且其还跟它的下一层 h + 1 h+1 h+1层的权值矩阵的转置 ( W h + 1 ) T (W^{h+1})^T (Wh+1)T以及跟 f ′ ( Y h − 1 W h ) {f}'(Y^{h-1}W^{h}) f′(Yh−1Wh)有关。
所以我们在使用BP算法的时候,需要先根据网络预测的误差计算最后一层的学习信号,其次再计算倒数第二层的学习信号,最后再计算倒数第三层的学习信号,以此类推,从后向前计算。因此BP算法叫做误差反向传播算法。计算得到每一层的学习信号以后,再根据权值调整的公式来计算每一层的权值矩阵如何调整,最后对所有层的权值矩阵进行更新。
使用BP神经网络求解异或问题
import numpy as np
import matplotlib.pyplot as plt
# 输入数据
X = np.array([[0,0],[0,1], [1,0],[1,1]])
# 标签
T = np.array([[0],[1],[1],[0]])
# 定义一个2层的神经网络:2-10-1
# 输入层2个神经元,隐藏层10个神经元,输出层1个神经元
# 输入层到隐藏层的权值初始化,2行10列
W1 = np.random.random([2,10])
# 隐藏层到输出层的权值初始化,10行1列
W2 = np.random.random([10,1])
# 初始化偏置值,偏置值的初始化一般可以取0,或者一个比较小的常数,如0.1
# 隐藏层的10个神经元偏置
b1 = np.zeros([10])
# 输出层的1个神经元偏置
b2 = np.zeros([1])
# 学习率设置
lr = 0.1
# 定义训练周期数
epochs = 100001
# 定义测试周期数
test = 5000
# 定义sigmoid函数
def sigmoid(x):
return 1/(1+np.exp(-x))
# 定义sigmoid函数导数
def dsigmoid(x):
return x*(1-x)
# 更新权值和偏置值
def update():
global X,T,W1,W2,lr,b1,b2
# 隐藏层输出
L1 = sigmoid(np.dot(X,W1) + b1)
# 输出层输出
L2 = sigmoid(np.dot(L1,W2) + b2)
# 根据公式4.41,求输出层的学习信号
delta_L2 = (T - L2) *dsigmoid(L2)
# 根据公式4.42,求隐藏层的学习信号
delta_L1 = delta_L2.dot(W2.T) *dsigmoid(L1)
# 根据公式4.44,求隐藏层到输出层的权值改变
# 由于一次计算了多个样本,所以需要求平均
delta_W2 =lr*L1.T.dot(delta_L2) /X.shape[0]
# 根据公式4.45,求输入层到隐藏层的权值改变
# 由于一次计算了多个样本,所以需要求平均
delta_W1 =lr*X.T.dot(delta_L1) / X.shape[0]
# 更新权值
W2 =W2 + delta_W2
W1 =W1 + delta_W1
# 改变偏置值
# 由于一次计算了多个样本,所以需要求平均
b2 =b2 +lr*np.mean(delta_L2, axis=0)
b1 =b1 +lr*np.mean(delta_L1, axis=0)
# 定义空list用于保存loss
loss = []
# 训练模型
for i in range(epochs):
# 更新权值
update()
# 每训练5000次计算一次loss值
if i %test == 0:
# 隐藏层输出
L1 = sigmoid(np.dot(X,W1) + b1)
# 输出层输出
L2 =sigmoid(np.dot(L1,W2) + b2)
# 计算loss值
print('epochs:',i,'loss:',np.mean(np.square(T - L2) / 2))
# 保存loss值
loss.append(np.mean(np.square(T - L2) / 2))
# 画图训练周期数与loss的关系图
plt.plot(range(0,epochs,test),loss)
plt.xlabel('epochs')
plt.ylabel('loss')
plt.show()
# 隐藏层输出
L1 = sigmoid(np.dot(X,W1) + b1)
# 输出层输出
L2 = sigmoid(np.dot(L1,W2) + b2)
print('output:')
print(L2)
# 因为最终的分类只有0和1,所以我们可以把
# 大于等于0.5的值归为1类,小于0.5的值归为0类
def predict(x):
if x>=0.5:
return 1
else:
return 0
# map会根据提供的函数对指定序列做映射
# 相当于依次把L2中的值放到predict函数中计算
# 然后打印出结果
print ('predict:')
for i in map(predict,L2):
print(i)
运行结果如下:
epochs: 0 loss: 0.21655021948422454
epochs: 5000 loss: 0.11886693767654921
epochs: 10000 loss: 0.0784134455934812
epochs: 15000 loss: 0.020728082691587067
epochs: 20000 loss: 0.006474064948643635
epochs: 25000 loss: 0.003216904125830181
epochs: 30000 loss: 0.0020068415981549523
epochs: 35000 loss: 0.0014139696548422505
epochs: 40000 loss: 0.0010726101163828885
epochs: 45000 loss: 0.0008545799251234986
epochs: 50000 loss: 0.0007049564200818229
epochs: 55000 loss: 0.0005967480043781333
epochs: 60000 loss: 0.0005153047148555323
epochs: 65000 loss: 0.0004520544201019757
epochs: 70000 loss: 0.00040167730296948004
epochs: 75000 loss: 0.00036071199148032226
epochs: 80000 loss: 0.00032681711228389016
epochs: 85000 loss: 0.0002983566300128549
epochs: 90000 loss: 0.00027415545154439193
epochs: 95000 loss: 0.00025334936598236956
epochs: 100000 loss: 0.0002352896211791448
output:
[[0.02123791]
[0.9775524 ]
[0.98023771]
[0.02316949]]
predict:
0
1
1
0