一 背景
近年来,随着大数据与人工智能的盛行,针对个人的个性化的推荐技术的不断发展,人们在享受便利的同时,也深深的感觉到无处不在的监控与监视,比如
- 刚刚浏览了一个网站的商品,当去其他网站访问的时候就会推荐类似的产品;
- 刚刚搜索了某件商品,在很多其他的场景中都会给你推荐。
这种体验,提供了一些便利,刚开始大家都感觉互联网非常智能化,但是如果仔细想想,就感觉自己的网上进行裸奔,你做了什么,别人都是一清二楚,个人信息毫无隐私可言,如果用这些信息进行诈骗等,会造成严重的损失,细思极恐。
不过随着广大用户对于个人隐私的重视程度不断加强,以及法律法规的不断完善,针对个人隐私的保护提出了更高的要求,什么样的数据可以采集、收集与使用,如何使用都是一个比较敏感的问题。十三届全国人大常委会第三十次会议表决通过了《中华人民共和国个人信息保护法》,并与2021年11月1日起施行。确立个人信息保护原则、规范处理活动保障权益、禁止“大数据杀熟”规范自动化决策、严格保护敏感个人信息、赋予个人充分权利等。新规施行后,违法的主体将最高可处五千万以下或者上一年度营业额百分之五以下的罚款。
鉴于上述情况,近年来隐私计算技术被不断的提及,源于其有优秀的数据保护作用,使得“数据不出域、数据可用不可见、数据可算不可见”,限定了数据的使用场景,防止了数据的泄露,而引起了业界的热捧。
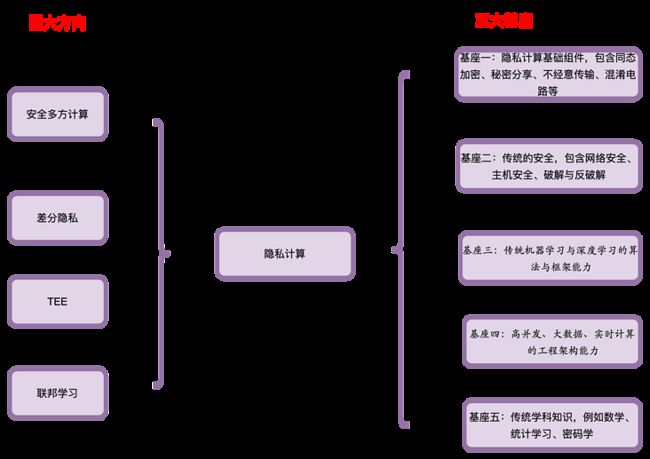
那么如何学习隐私计算呢?笔者认为这门技术是门综合性非常强的领域,涉及到众多方向,比如密码学、数学、大数据、实时计算、高性能计算、分布式、传统机器学习框架与算法,深度学习框架与算法等等,整体技术非常复杂,对于从业者的要求极高。根据目前市场上隐私计算的主要相关技术特性,可分为四大方向与五大基座::
《隐私计算基础组件》系列文章会和大家一起介绍下基座二:隐私计算的基础技术,本章主要介绍重要的基础组件:混淆电路的第一部分。;
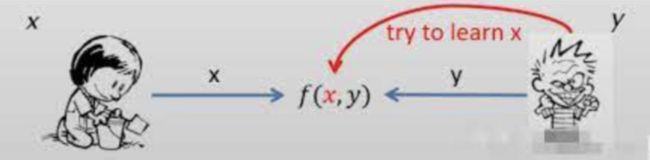
二 安全模型的定义
在隐私计算的场景中,根据各个参与方的可信程度可以定义三种安全模型,用于描述在隐私计算过程中的可信程度度量与定义。
- Real-Ideal Paradigm(理想模型) :在理想模型中,每一个参与方都是可信的,一方将其信息发送给另一方,另一方不会去查看这份信息,只会根据规定计算出结果,并发送给下一方或者所有参与方。
- Semi-Honest Security(半诚实模型) :半诚实模型就是参与方会诚实的运行协议,但是他会根据其它方的输入或者计算的中间结果来推导额外的信息。
- Malicious Security(恶意模型) :恶意模型则可能不会诚实的运行协议,甚至会搞破坏。
在现实世界中,理性模型是不存在的,但相比于恶意模型,参与方其实更想真的想获取到对自己有用的信息以及以外更多的信息(比如推导中间计算环节),所以多数情况下符合半诚实模型。因此下面的讨论都是基于半诚实模型下的。
三 前置知识 - 不经意传输
不经意传输:针对不经意传输的详细的解释,请看我以前写的文章 隐私计算基础组件系列-不经意传输
这里在简单说下,对于不经意传输,我个人认为有几点比较重要:
- 需要参与运算的元素的个数是确定的;
- 需要参与运算的元素的顺序是相对固定的;
- 异或操作的可逆性;
流程:
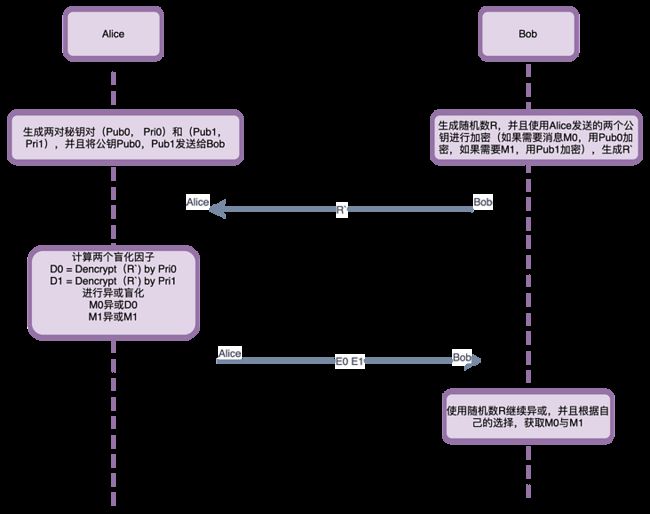
- 第一步:消息发送者Alice有两个待发送消息M0与M1。生成两对RSA秘钥对,然后将两个公钥Puk0、Puk1发送给接受者Bob。
第二步:Bob生成一个随机数R,并用收到的两个公钥之一加密随机数R,用哪个秘钥取决于Bob想获取M0还是M1(参照百万富翁的案例,这个时候需要知道顺序或者标记)
- 如果想要得到消息M0,就用Puk0加密随机数R生成$R^
$,并将密文结果$R^$发送给Alice。 - 如果想要得到消息M1,就用Puk1加密随机数R生成$R^
$,并将密文结果$R^$发送给Alice。
- 如果想要得到消息M0,就用Puk0加密随机数R生成$R^
- 第三步:Alice生成的两对秘钥对的私钥(Pr0,Pr1)分别解密收到随机数密文(只有一个还原了随机数,但是Alice不知道是哪个),并得到两个解密结果(D0,D1),并将两个解密结果(D0,D1)分别与要发送的两条信息进行异或(D0异或M0,D1异或M1,注意不是笛卡尔积,是按照协议顺序来进行异或操作),并将两个结果E0,E1按照协议顺序发给Bob。
- 第四步:Bob用以前生成的随机数R与收到的E0或E1分别做异或操作(如果要获取M0消息就异或E0,如果要获取M1消息就异或E1),得到最终的结果。
四 混淆电路(Garbled Circuits,GC)
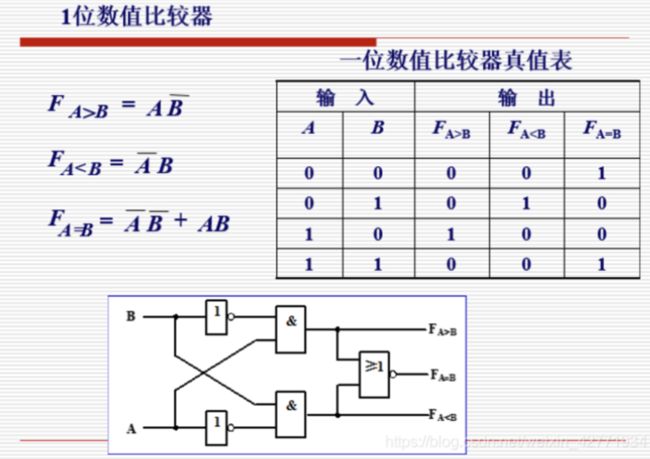
如上图所示,里面我们的两个老朋友Alice和Bob想要搞点事情,还是比较谁更富有,但是不希望互相公布自己的财富值。这次我们不适用秘密分享、不经意传输来解决,我们将问题转化为数字电路来解决(比如比较电路,或者emmmm什么电路)。电路里面有一些门,每个门包括输入线(input wire)和输出线(output wire)。混淆电路就是通过加密和调整序列的值来掩盖信息的。在最经典的混淆电路中,加密和扰乱是以门为单位的。每个门都有一张真值表。
混淆电路具体是什么含义呢?其实从他的名字我们可以得出一个结论,他一定是用到了电路(数字电路),我们推断他应该是将原始的多维混合运算转化为一个一个的简单的基础电路,继而进行组合,得到最后的结果。同时由于在运算的过程中,需要针对运算各方进行隐私保护,所以使用了不经意传输的隐私计算技术进行增强,最终得到最后的结果。
运算的性能随着是由整体原始的运算量决定的,由于采用的是不经意传输的技术,所以相对于同态加密这种耗时耗力的模式,性能还是可以接受的。
4.1 场景设定
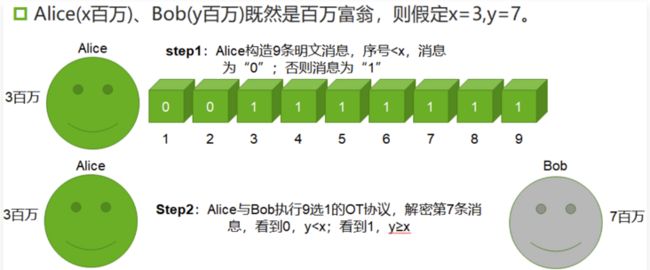
假设场景里面的人物仍然是我们的老朋友Alice和Bob,两个人接着进行炫富比较,这两个人假设都是百万富翁,在某个较为私密的场合,他们想比较下谁更加富有,但是又不想让对方知道彼此具体的财富值。
这个问题我们在前面介绍过,使用不经意传输是可以解决的,而且算法协议也和大家分享过,这里我们不直接使用不经意传输进行解决,而是使用混淆电路。
假设,我们设定Alice的财富值是X,Bob的财富值是Y,那么我们就是要求解X与Y谁大的问题,那么这个问题如何转化为混淆电路问题呢?
关键就在这个电路上,我们接着看。
4.2 数字电路转化
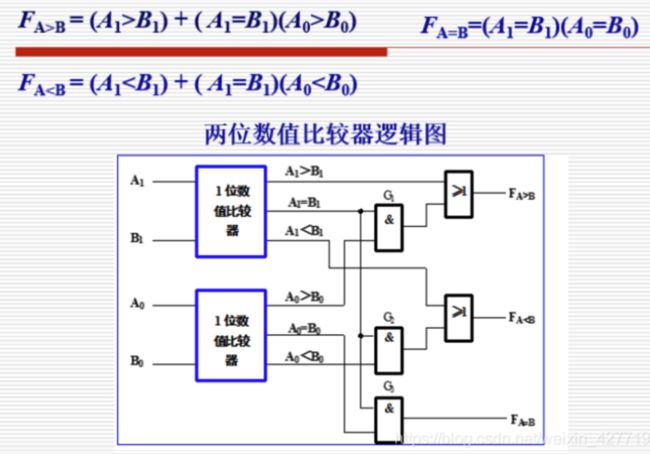
在使用混淆电路之前,需要先对原始问题进行数字电路表达。我们知道可计算问题都可以转换为一个个电路,于是就有了加法电路、比较电路和乘法电路等等。当然,更复杂的计算过程,如深度学习等等,也是可以转换成电路的,只不过转换后的电路较为复杂与庞大。一个电路是由一个个门(gate)组成的,比如与门、非门、或门、与非门等等。
数字电路是有一些简单的门(比如与门、非门、或门、与非门等等)组合而成,输入是0、1的数值,将一个复杂的运算替换成若干个简单的门(gate)的组合。
对于上面的问题,我们看下对应的数字电路是如何进行电路转化的。
由此可见,通过将运算转化成数字电路是可行的,并且转化后需要一个真值表和多个门。
本文并不打算过多介绍数字电路的知识,有兴趣的读者可以去看下《数字电路》这本书,所以本文设定一个门与相应的真值表进行讲解,请大家继续往下看。
4.3 算法协议
这里我们针对与门进行讲解,整体流程主要包含四大步骤。
第一步:Alice 生成混淆电路
- 首先,Alice生成电路的Truth Table,并且对于真值表按照与门进行计算标注(如下图所示)。
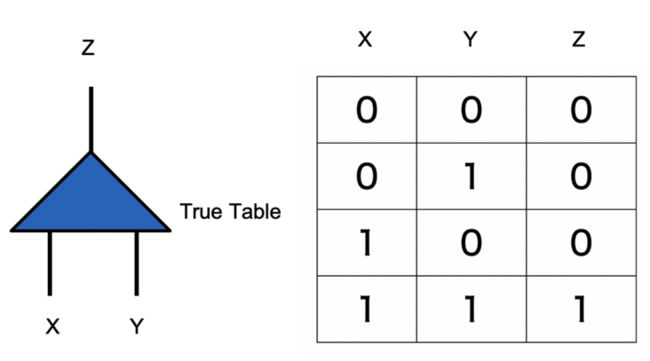
- 然后,Alice进行电路的Truth Table替换(替换值代替真实值,对真实值进行隐藏),例如输入$X_0$代表X=0,输入$X_1$代表X=1,输入$Y_0$代表Y=0,输入$Y_1$代表Y=1,输出$Z_0$代表Z=0,输入$Z_1$代表Z=1(这些值,我们称之为替换值,随机生成,无规律;原始的输入称之为真实值)。
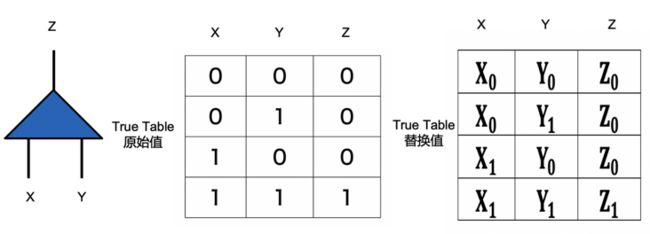
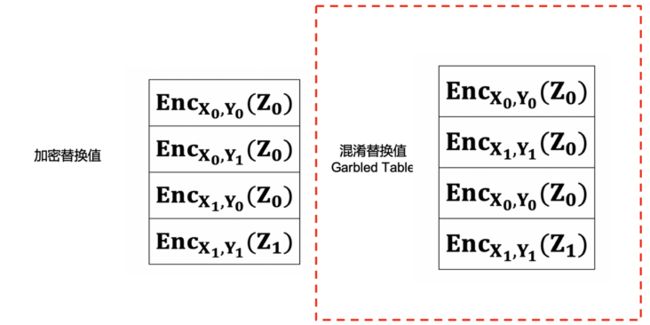
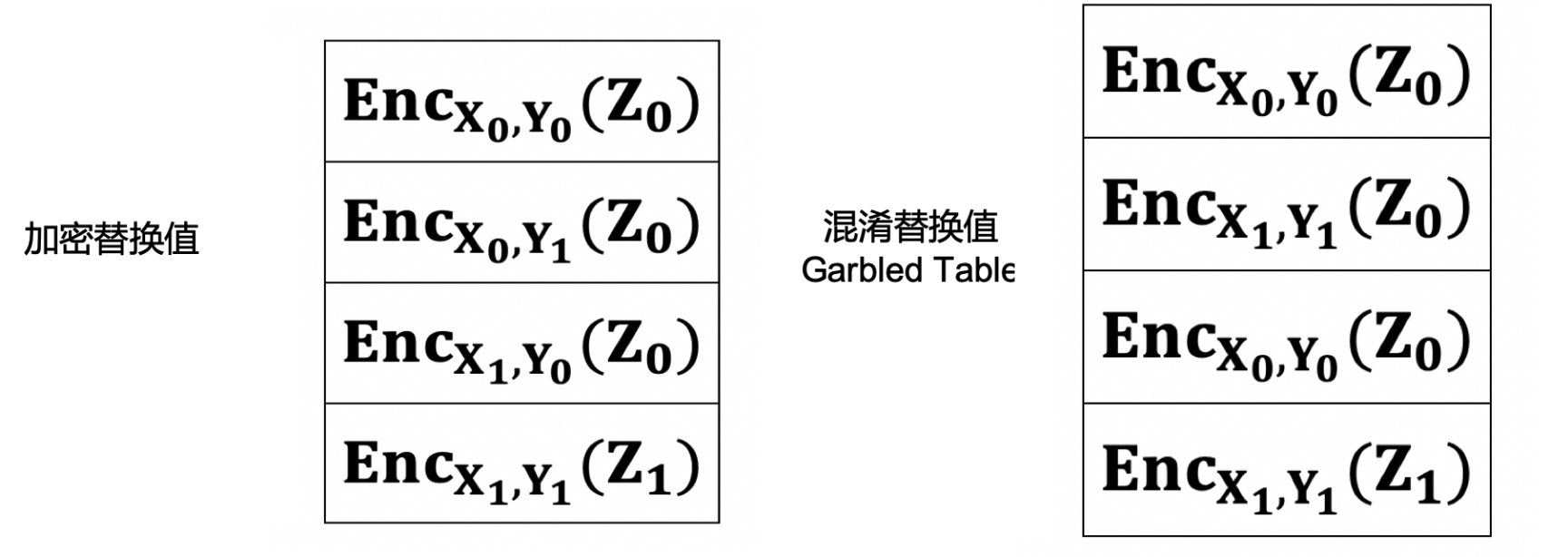
然后,Alice针对替换后的Truth Table的输出进行两次对称加密(加密与加密的秘钥相同),并且加密的秘钥分别是Truth Table的两个输入。比如Truth Table的某行两个输入分别是$X_0$与,输出是$Z_0$,那么替换后的真值表的某行就是$Enc_{X_0, Y_1}(Z_0)$;
- 然后,Alice将加密过后的 Truth Table 的行打乱得到 Garbled Table。所以 Garbled Table 的内容和行号就无关了。这越是混淆电路中的混淆二字的由来。
- 首先,Alice生成电路的Truth Table,并且对于真值表按照与门进行计算标注(如下图所示)。
第二步: Alice 和 Bob 通信
- 首先,Alice将自己的输入发送给 Bob。比如取输入$X=0$,Alice就会发送替换值$X_0$给 Bob。由于 Bob 只是收到$X_0$对应的替换值,也就无从知晓 Alice 的原始值了。
- 然后,Bob通过不经意传输协议,从 Alice 那里获得他的输入对应的替换值,并且通过协议,可以让Alice不知道Bob具体使用的是那个原始值,这里假设Bob的输入是1,所以通过不经意传输最终获取$Y_1$的替换值。具体流程:通过不经意传输协议保证了 Bob 在替换值$Y_0, Y_1$中获得一个,但是Alice并不知道Bob获得了哪一个。(具体流程可以参加 隐私计算基础组件系列-不经意传输)
然后,Alice 将与门的 Garbled Table发给 Bob。在这个例子中,一共有四个 Garbled Table。
第三步,Bob evaluate混淆电路
- 首先,Alice和Bob通信完成之后,Bob尝试进行电路解密,目前Bob已知的信息有输入$X_0$和$Y_1$,所以使用这两个值,对于Garbled Table的四行进行解密,可以看到,这里只有第三行是可以解密成功的。
- 然后,Bob虽然解密成功,但是由于解密出的$Z_0$仍然是替换值(非原始值0),所以无法获得其他信息。
第四步,Alice和Bob共享结果
- 最后 Alice 和 Bob 共享结果。Bob分享解密后替换值结果$Y_0$给Alice,Alice知道替换值与原始值的替换关系,进行替换,并且可以将最终结果分享给Bob。
一个与门的混淆电路流程到此已经分享完毕,由于现实中使用的运算较为复杂,所以涉及到将运算转化成数字电路,并且将数字电路优化的过程,最终分解成一个一个的门。所以想对这块有深入钻研的同学,需要对数字电路多下些功夫。
但是万变不离其宗,所有的复杂的事情都是简单的构成,相信大家在熟悉了上面的流程的基础上,对于混淆电路会有一个正确的认知。
五 参考资料
- [1] A. Yao. Protocols for secure computations. In Proceedings of the 23rd Annual Symposium on Foundations of Computer Science, SFCS ’82, pages 160–164, 1982.
- [2] A. Yao. How to generate and exchange secrets. In Proceedings of the 27th Annual Symposium on Foundations of Computer Science, SFCS ’86, pages 162–167, 1986.
- [3] O. Goldreich, S. Micali, and A. Wigderson. How to play any mental game. In Proceedings of the Nineteenth Annual ACM Symposium on Theory of Computing, STOC ’87, pages 218–229, 1987.
- [4] D. Bogdanov, R. Talviste, and J. Willemson. Deploying secure multi-party computation for financial data analysis. In Financial Cryptography and Data Security: 16th International Conference, FC 2012, Kralendijk, Bonaire, Februray 27-March 2, 2012, Revised Selected Papers, pages 57–64, 2012.
- [5] Y. Lindell and B. Pinkas. Secure multiparty computation for privacy-preserving data mining. The Journal of Privacy and Confidentiality, 1(1):59–98, 2009.
- [6] B. Hemenway, S. Lu, R. Ostrovsky, and W. Welser IV. High-precision secure computation of satellite collision probabilities. In Security and Cryptography for Networks: 10th International Conference, SCN 2016, Amalfi, Italy, August 31 – September 2, 2016, Proceedings, pages 169–187, 2016.
- [7] R. Cramer, R. Gennaro, and B. Schoenmakers. A secure and optimally efficient multi-authority election scheme. In Advances in Cryptology — EUROCRYPT ’97: International Conference on the Theory and Application of Cryptographic Techniques Konstanz, Germany, May 11–15, 1997 Proceedings, pages 103–118, 1997.
- [8] P. Bogetoft, D. Christensen, I. Damgård, M. Geisler, T. Jakobsen, M. Krøigaard, J. Nielsen, J. Nielsen, K. Nielsen, J. Pagter, M. Schwartzbach, and T. Toft. Financial cryptography and data security. chapter Secure Multiparty Computation Goes Live, pages 325–343, 2009.
- [9] M. Naor, B. Pinkas, and R. Sumner. Privacy preserving auctions and mechanism design. In Proceedings of the 1st ACM Conference on Electronic Commerce, EC ’99, pages 129–139, 1999.
- [10] R. Kulkarni and A. Namboodiri. Secure hamming distance based biometric authentication. In 2013 International Conference on Biometrics (ICB), pages 1–6, June 2013.
- [11] J. Bringer, H. Chabanne, and A. Patey. Shade: Secure hamming distance computation from oblivious transfer. In Financial Cryptography and Data Security: FC 2013 Workshops, USEC and WAHC 2013, Okinawa, Japan, April 1, 2013, Revised Selected Papers, pages 164–176, 2013.
- [12] M. Kiraz, Z. Genç, and S. Kardaş. Security and efficiency analysis of the hamming distance computation protocol based on oblivious transfer. Security and Communication Networks, 8(18):4123–4135, 2015.
- [13] J. Launchbury, D. Archer, T. DuBuisson, and E. Mertens. Application-scale secure multiparty computation. In Programming Languages and Systems: 23rd European Symposium on Programming, ESOP 2014, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2014, Grenoble, France, April 5-13, 2014, Proceedings, pages 8–26, 2014.
- [14] O. Biçer. Efficiency Optimizations on Yao’s Garbled Circuits and Their Practical Applications. Cryptography and Security, 2017.
- [15] O. Goldreich. Cryptography and Cryptographic Protocols. Distributed Computing – Papers in Celebration of the 20th Anniversary of PODC, 16 (2–3): 177–199, 2003.
- [16] Beaver D, Micali S, Rogaway P, et al. The round complexity of secure protocols[C]. In Proceedings of the Twenty-second Annual ACM Symposium on Theory of Computing, STOC ’90, pages 503–513, 1990.
六 番外篇
个人介绍:杜宝坤,隐私计算行业从业者,从0到1带领团队构建了京东的联邦学习解决方案9N-FL,同时主导了联邦学习框架与联邦开门红业务。
框架层面:实现了电商营销领域支持超大规模的工业化联邦学习解决方案,支持超大规模样本PSI隐私对齐、安全的树模型与神经网络模型等众多模型支持。
业务层面:实现了业务侧的开门红业务落地,开创了新的业务增长点,产生了显著的业务经济效益。
个人比较喜欢学习新东西,乐于钻研技术。基于从全链路思考与决策技术规划的考量,研究的领域比较多,从工程架构、大数据到机器学习算法与算法框架均有涉及。欢迎喜欢技术的同学和我交流,邮箱:[email protected]
七 公众号导读
自己撰写博客已经很长一段时间了,由于个人涉猎的技术领域比较多,所以对高并发与高性能、分布式、传统机器学习算法与框架、深度学习算法与框架、密码安全、隐私计算、联邦学习、大数据等都有涉及。主导过多个大项目包括零售的联邦学习,社区做过多次分享,另外自己坚持写原创博客,多篇文章有过万的阅读。公众号秃顶的码农大家可以按照话题进行连续阅读,里面的章节我都做过按照学习路线的排序,话题就是公众号里面下面的标红的这个,大家点击去就可以看本话题下的多篇文章了,比如下图(话题分为:一、隐私计算 二、联邦学习 三、机器学习框架 四、机器学习算法 五、高性能计算 六、广告算法 七、程序人生),知乎号同理关注专利即可。
![]()
一切有为法,如梦幻泡影,如露亦如电,应作如是观。
本文由mdnice多平台发布