聊聊动态规划之BFS/DFS+剪枝——以滑雪问题为例
目录
- BFS + 剪枝
-
- 使用BFS解决滑雪问题
- DFS + 剪枝
-
- 使用DFS解决滑雪问题
- 二者执行顺序的比较
- 结论
BFS + 剪枝
首先让我们看看BFS是个什么样的运作原理:
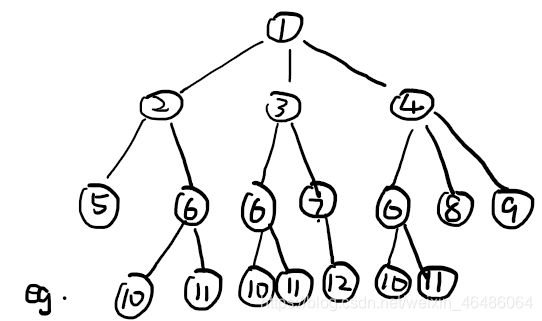
BFS是以广度为优先,也就是先把同级的每一个节点(例如2)先进行运算,同时将和它相邻的需要运算的节点入队,稍后再算(例如2对应的5、6),当同级的所有节点都运算完了的时候(2、3、4),由于队列先进先出的特点,自然轮到了下一级节点(5、6、7、8、9)
然后再看看在BFS中,树是如何剪枝的:

在很多问题中(尤其是棋盘移动之类的),会出现多个节点连上同一个节点的情况(如图中的2、3、4都连着下一级的6),这时候根据条件判断哪一条更优。例如图中红色数值越大越优,当判断到2连6的数字是20时,6的红色值被赋予20,与2相连;当判断到3连6的数字是30时,30比20大,6的红色值被赋予30,与3相连;当判断到4连6的数字是10时,10比30小,6的红色值不变,仍然与3相连;这样,就剪断了2和6,4和6的枝。
使用BFS解决滑雪问题
Michael喜欢滑雪,这并不奇怪, 因为滑雪的确很刺激。可是为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,你不得不再次走上坡或者等待升降机来载你。Michael想知道载一个区域中最长底滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
一个人可以从某个点滑向上下左右相邻四个点之一,当且仅当高度减小。在上面的例子中,一条可滑行的滑坡为24-17-16-1。当然25-24-23-…-3-2-1更长。事实上,这是最长的一条。
输出最长区域的长度,本例中是 25。
先上代码吧:
#include 首先定义好高度的二维数组,以及用来存到某一点所需步数的临时二维数组;为了代码简洁,同时定义好含四个方向的数组,以及包含着x、y坐标和已经移动的步数的point结构(并且写好构造函数)
主要思路是这样的:
遍历所有的起点
–清空临时数据
–检测起点的可移动信息,并将可以去的下一个点入队(函数bfs())
–队列非空时,对每个元素再检测可移动信息,并将下一个点入队(函数bfs())
–计入每个起点最终的最大移动步数
函数bfs的思路:
遍历四个方向的下一个点进行测试
–判断该方向下一个点是否还在二维数组中
—-判断下一个点的高度是否比当前点更小
——判断下一个点是否没有别的路径到达过,或者有但是路径比正在测试的路径短(注意:这里正是树剪枝的办法,直接剪掉不可能是最长的路径)
——–如果均为是,将下一个可以到达的点入队,并且更新步数的表格
遍历完之后,总步数+1(因为最后一次无路可走也会导致步数+1,最终结果要-1)
样例输出:

首先,最终结果输出的是25,也就是从(2,2)点的“25”开始出发的最长路径。
然后以图上的(4,4),既“9”为原点为例,可以看出探索的路径:
最初在起点(4,4),判断到下一个存在的点有(3,4)和(4,3),挑选出没有经过过、并且高度更低的点(3,4),再判断存在的点(4,4),(2,4)和(3,3)。因为高度只能下降,可以没有必要去把曾经经过的点标记为已经过。通过多次测试,最终按照9、8、7、6、5、4、3、2、1的顺序找到了步数为9的最大路径。
DFS + 剪枝
下面接着同样的思路,对DFS同样进行剪枝

DFS是以深度为优先的搜索方式,先沿着一枝探索到底,然后逐枝从探索过的节点回溯,再探索下一枝。这种情况下,后进先出的栈更适合存储节点信息。同样地,在选取了某个曾经到达过的节点时,判断这枝是否优先度更高,从而保留或者更新枝,达到剪枝的效果。
使用DFS解决滑雪问题
接着上一段同样滑雪问题的DFS解法代码:
#include }
几乎没有做改变,仅仅是用栈替换了队列,来存储将要读取的信息。同样,输出的结果依然是25,不过,从中间的步骤可以看出二者的区别。
二者执行顺序的比较
我们同样以(2,2)为起点,比较一下二者所探索的点的不同之处:
BFS
正在以(2,2)为起点
正在点(2,2)
正在测试有效点(3,2)高度
正在测试有效点(2,3)高度
正在测试有效点(1,2)高度
正在测试有效点(2,1)高度
正在点(3,2)
正在测试有效点(4,2)高度
正在测试有效点(3,3)高度
正在测试有效点(2,2)高度
正在测试有效点(3,1)高度
正在点(2,3)
正在测试有效点(3,3)高度
正在测试有效点(2,4)高度
正在测试有效点(1,3)高度
正在测试有效点(2,2)高度
正在点(1,2)
正在测试有效点(2,2)高度
正在测试有效点(1,3)高度
正在测试有效点(0,2)高度
正在测试有效点(1,1)高度
正在点(2,1)
正在测试有效点(3,1)高度
正在测试有效点(2,2)高度
正在测试有效点(1,1)高度
正在测试有效点(2,0)高度
正在点(4,2)
正在测试有效点(4,3)高度
正在测试有效点(3,2)高度
正在测试有效点(4,1)高度
正在点(3,3)
正在测试有效点(4,3)高度
正在测试有效点(3,4)高度
正在测试有效点(2,3)高度
正在测试有效点(3,2)高度
正在点(2,4)
正在测试有效点(3,4)高度
正在测试有效点(1,4)高度
正在测试有效点(2,3)高度
正在点(1,3)
正在测试有效点(2,3)高度
正在测试有效点(1,4)高度
正在测试有效点(0,3)高度
正在测试有效点(1,2)高度
......

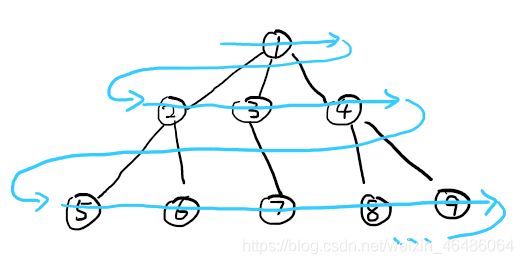
正如图中,程序先按下、右、上、左的顺序发现四个红箭头都可以前往;然后先按下的红箭头到达队列中的第一个点,判断两个蓝箭头均可前往;接着按右的红箭头到达队列中的第二个点,本来绿箭头应该先到达黄色高亮的点,然而已经判断到了蓝箭头已曾到达过这个点了,并且绿箭头到达黄点也并不更优,于是剪断了这根枝,绿箭头只到达了右边和上面的点。
DFS
正在点(2,2)
正在测试有效点(3,2)高度
正在测试有效点(2,3)高度
正在测试有效点(1,2)高度
正在测试有效点(2,1)高度
正在点(2,1)
正在测试有效点(3,1)高度
正在测试有效点(2,2)高度
正在测试有效点(1,1)高度
正在测试有效点(2,0)高度
正在点(2,0)
正在测试有效点(3,0)高度
正在测试有效点(2,1)高度
正在测试有效点(1,0)高度
正在点(3,0)
正在测试有效点(4,0)高度
正在测试有效点(3,1)高度
正在测试有效点(2,0)高度
正在点(4,0)
正在测试有效点(4,1)高度
正在测试有效点(3,0)高度
正在点(4,1)
正在测试有效点(4,2)高度
正在测试有效点(3,1)高度
正在测试有效点(4,0)高度
正在点(4,2)
正在测试有效点(4,3)高度
正在测试有效点(3,2)高度
正在测试有效点(4,1)高度
正在点(4,3)
正在测试有效点(4,4)高度
正在测试有效点(3,3)高度
正在测试有效点(4,2)高度
正在点(4,4)
正在测试有效点(3,4)高度
正在测试有效点(4,3)高度
……

对于DFS,因为栈后进先出,所以按相反的顺序测试点,即左、上、右、下。判断时,点先按第一条路走到底,也就是红箭头一直走到(0,0)处后,再沿着树回溯。跳过一些步骤举例,例如回溯到黄色高亮点往蓝箭头方向搜索时,蓝箭头本来优先探索左方向,然而已经判断到了红箭头已曾到达过这个点了,并且蓝箭头到达这个点也并不更优,于是同样地剪断了这根枝,蓝箭头只能跳过向左,先向右进行搜索。
结论
动态规划利用存储已经运算过的内容,避免了对某些运算内容的重复运算,从而达到了减少运算量的目的。这是一种优化力度大,通用性强的计算机算法、以至数学方法。