算法模板：高级数据结构之树状数组

本文已收录于专栏 ⭐️ 《算法通关笔记》⭐️

前言

⭐️感谢相遇，唤我沈七就好。
⭐️如果能和你一起进步那就太好啦。

树状数组

引入

如果 给出一个长度为n的数组，想快速完成以下两种操作：

1. 将第i个数加上k
2. 输出区间[i,j]内每个数的和

如果之前学过的用线性前缀和算法的话。

单点修改：O(1)
区间查询：O(n)

这时我们发现 区间查询 O(n) 的时间 极大的拖累了整个操作的时间复杂度。

那如何更快速解决以上问题呢？

这时便引用了出了树状数组，即使用树结构维护”前缀和”，从而把时间复杂度降为O(logn)。

前置知识

在讲树状数组之前，我们需要先掌握 lowbit（）函数的概念与用法。
$$lowbit（x）：函数返回值位x二进制表示中最后一个1的位置。$$
举例说明：
$$lowbit(12)=lowbit([1100]2)=[100]2=4$$
解释： 12 的二进制表示为 1100 ，最后一位1的次数是右数第 2 位（从第0位算起），所以 lowbit 返回值 是 2 的 2 次方。

我们将 x 用二进制来表示。

并将 x 划分成以下区间。

如图，我们发现 每个的区间长度都是 右端点 二进制表示的最后一个 1，即 lowbit（r）。

例如：第一个区间的长度是 x 二进制中最后一个1对应的次幂 即 2^0

​ 第二个区间的长度是 (x - 2^0 ) 二进制中最后一个1对应的次幂 即 2^ 1

​ 第三个区间的长度是 (x - 2^0 - 2^1 )二进制中最后一个1对应的次幂 即 2^ 2

​ 以此类推。

这是我们 lowbit 函数就派上用场了，可以很自然的将区间 [L,R] 的长度 表示成 lowbit（R）。
$$则(L,R]可以表示为[R-lowbit[R]+1,R],t[x]表示该区间的总和,t[x]=a[x-lowbit(x)+1,x]$$
即以x为右端点的长度是lowbit(x)的区间内所有数的和

我们可以以 区间的长度为二进制表示的最后一位的性质 来画出以下的树形结构，即树状数组。

解读：

len1 = 1 ：0001 即 最后一位是 0 位，区间长度为 2 ^ 0 = 1

len2 = 2 ：0010 即 最后一位是 1 位，区间长度为 2 ^ 1 = 2

len3 = 4 ：0100 即 最后一位是 2 位，区间长度为 2 ^ 2 = 4

树状数组操作

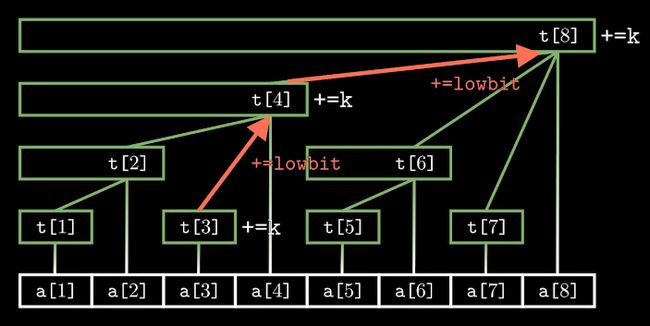
• add(x, k)表示将序列中第x个数加上k。即单点修改。

以add(3, 5)为例：
在整棵树上维护这个值，需要一层一层向上找到父结点，并将这些结点上的t[x]值都加上k，这样保证计算区间和时的结果正确。时间复杂度为O(logn)

void add(int x, int k)
{
    for(int i = x; i <= n; i += lowbit(i))
        t[i] += k;
}

• ask(x)表示将查询序列前x个数的和

以ask(7)为例：

查询这个点的前缀和，需要从这个点向左上找到上一个结点，将加上其结点的值。

向左上找到上一个结点，只需要将下标 x -= lowbit(x)，例如 7 - lowbit(7) = 6。

int ask(int x)
{
    int sum = 0;
    for(int i = x; i; i -= lowbit(i))
        sum += t[i];
    return sum;
}

单点修改 区间查询

如题，已知一个数列，你需要进行下面两种操作：

• 将某一个数加上 xxx
• 求出某区间每一个数的和

#include  
using namespace std;
typedef long long LL;
int n,m;
const int N = 2e5+10;
LL ans,res;
int a[N],t[N];
int lowbit(int x){
    return x&-x;
}
void add(int x,int k)
{
    for(int i = x ; i <= n ;i +=lowbit(i))t[i]+=k;
}
int ask(int x)
{
    if(x==0) return 0;
    int sum = 0 ;
    for(int i = x ; i ; i -=lowbit(i))sum+=t[i];
    return sum;
}
int main()
{
    cin>>n>>m;
    for(int i = 1 ;i <= n ;i ++)
    {
        int x;
        cin>>x;
        add(i,x);
    }
 	for(int i=1;i<=m;++i)
	{
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		if(x==1)
		{
			add(y,z); 
		}
		if(x==2)
		{
			int end=ask(z)-ask(y-1);
			printf("%d\n",end);
		}
		 
	}
    return 0 ; 
}

差分树状数组

区间修改 单点查询

差分+树状数组

区间修改 : 差分思想

单点查询 : 差分树状数组的前缀和

第一类指令形如 C l r d，表示把数列中第 l∼r 个数都加 d。

第二类指令形如 Q x，表示询问数列中第 x 个数的值。

对于每个询问，输出一个整数表示答案。

#include
using namespace std;
const int N = 1e5+10;
int a[N],t[N];
int n,m;
int lowbit(int x)
{
    return x&-x;    
}
void add(int x,int k)
{
    for(int i = x ; i <= n ; i+=lowbit(i))t[i]+=k;
}
int sum(int x)
{
    int res = 0;
    for(int i = x ; i ; i -=lowbit(i))res+=t[i];
    return res;
}
int main()
{

    cin>>n>>m;

    for(int i = 1 ; i <= n ; i ++)scanf("%d",&a[i]);

    for(int i = 1 ; i <= n ; i ++)add(i,a[i]-a[i-1]);

    while(m--)
    {
        int l,r,d;
        string op;
        cin>>op;
        if(op=="C")
        {
            scanf("%d%d%d",&l,&r,&d);
            add(l,d),add(r+1,-d);
        }
        if(op=="Q")
        {
            scanf("%d",&l);
            printf("%d\n",sum(l));
        }
    }

    return 0;
}

区间查询 区间修改

差分树状数组 + 推公式

给定一个长度为 N 的数列 A，以及 M

条指令，每条指令可能是以下两种之一：

1. C l r d，表示把 A[l],A[l+1],…,A[r] 都加上 d
2. Q l r，表示询问数列中第 l∼r个数的和。

对于每个询问，输出一个整数表示答案。

#include
using namespace std;
typedef long long LL;
const int N= 1e5+10;
int n,m;
int a[N];
LL tr1[N];
LL tr2[N];
int lowbit(int x)
{
    return x &-x;
}
void add(LL tr[],int x,LL c)
{
    for(int i = x ; i <= n; i +=lowbit(i))tr[i]+=c;
}
LL sum(LL tr[],int x)
{
    LL res = 0;
    for(int i = x ; i ; i -= lowbit(i)) res+= tr[i];
    return res;
}
LL prefix_sum(int x)
{
    return sum(tr1,x) * (x+1) - sum(tr2,x);
}
int main()
{
    cin>>n>>m;
    for(int i = 1 ; i <= n ; i ++)cin>>a[i];

    for(int i = 1 ; i <= n ;i ++)
    {
        int b = a[i] - a[i -1 ];
        add(tr1,i,b); 
        add(tr2,i,(LL)b*i);
    }
    while(m--)
    {
        char op[2];
        int l,r,d;
        cin>>op>>l>>r;
        if(*op == 'Q')
          printf("%lld\n", prefix_sum(r) - prefix_sum(l - 1));
        else
        {
            cin>>d;
            add(tr1,l,d),add(tr2,l,l*d);
            add(tr1,r+1,-d),add(tr2,r+1,(r+1)*-d);
        }
    }
    return 0;
}

完结散花

ok以上就是对 高级数据结构之树状数组 的全部讲解啦，很感谢你能看到这儿。如果有遗漏、错误或者有更加通俗易懂的讲解,欢迎小伙伴私信我，我后期再补充完善。

参考文献

https://www.acwing.com/activity/content/19/
https://www.acwing.com/solution/content/13818/