ESWC 2018 | R-GCN：基于图卷积网络的关系数据建模

前言

题目： Modeling Relational Data with Graph Convolutional Networks
会议： Extended Semantic Web Conference, 2018
论文地址：Modeling Relational Data with Graph Convolutional Networks

本篇文章是GCN的作者Kipf继GCN后的一项工作，GCN存在以下两个比较明显的问题：

1. 只能处理无向图
2. 只能处理同质图，也就是只能处理同种类型的边。

R-GCN作为GCN的后续工作，其最主要的贡献就是将GCN引入到了多关系异质图中，也就是说R-GCN在对节点特征进行更新时可以考虑到不同类型边上节点的特征。

1. 关系图卷积网络

术语定义：网络$G=(\mathcal{V},\mathcal{E},\mathcal{R})$，其中节点$v_i\in \mathcal{V}$，边$(v_i,r,v_j)\in \mathcal{E}$，其中$r\in \mathcal{R}$表示边的类型。

GCN和R-GCN都是利用图卷积来更新节点状态，二者可以用以下框架统一起来：

这里$h_i^{(l)}$表示节点$v_i$第$l$层的隐状态，$g_m(.,.)$可以理解为前面文章提到的消息函数，${\mathcal{M}}_i$指节点$v_i$的传入消息集合，$\sigma$为激活函数。

对于GCN来讲，$g_m(.,.)$表示将邻居节点的特征乘上归一化权重系数，此时GCN并没有考虑节点的类型信息，因为所有节点都属于同一类型。

对于R-GCN来讲，一个关键问题是如何在卷积过程中考虑到不同类型节点间的不同之处，也就是多关系间如何进行交互。对于图中不同类型的关系，R-GCN的做法如下：

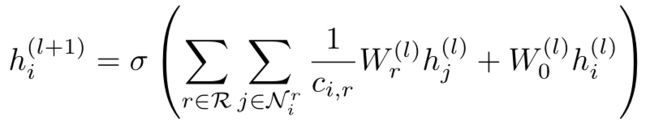
其中：

• ${\mathcal{N}}_i^r$：节点$v_i$的关系为$r$的邻居节点集合。比如对于一个引用网络而言，作者节点和其他节点的关系可能为“作者写论文”、“作者属于某一个组织”等等。
• $c_i,r$为一个归一化系数，可以设置为一个可学习的参数或者一个常量，例如$|{\mathcal{N}}_i^r|$。
• $W_r^{(l)}$为线性转换函数，观察下标$r$我们可以知道，每种类型的关系都有属于自己的线性函数，它们负责将对应关系边上的邻居节点的特征进行转换。

观察上式我们可以发现，R-GCN在将不同关系的节点特征进行聚合后，还需要加上本身节点的特征，最后通过一个激活函数以得到更新后的节点特征。

R-GCN与GCN最大的不同在于R-GCN引入了多个线性转换函数来对多种类型的关系节点进行转换，而GCN中只存在一种类型的关系，也就是只有一个线性转换函数。

R-GCN中单个节点更新的计算图如下所示：

其中红色节点表示待更新节点，深蓝色节点表示待更新节点的邻居节点，它们根据关系被分为不同的组，同时每组内的节点又根据边的方向分为对内关系节点和对外关系节点。深蓝色节点的状态通过转换函数进行转换后变成绿色的节点，然后再聚合到一起(由于为每个节点增加了self-loop，红色节点本身的特征也被考虑在内)。最后，聚合后的特征通过一个激活函数得到红色节点更新后的状态。

2. 正则化

R-GCN中需要为每一种类型的边指定一个转换函数$W$，如果一个网络拥有很多种关系，那么R-GCN中参数的数量也会急剧增长，造成巨大的计算开销。

为了解决这个问题，一个直观的想法是不同类型关系的转换函数共享参数，不过如果完全共享参数那R-GCN将退化为GCN。为此，作者提出了basis function decomposition，即基函数分解：

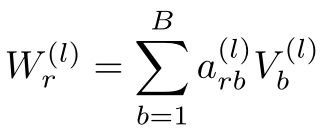
从基函数分解公式可看出，不同关系$r$的转换函数通过一个线性组合来得到，第$l$层中不同关系的转换函数的$V_b^{(l)}$相同，只是组合系数$a_{rb}^{(l)}$不同，这大大减少了参数数量。

文中作者还提出了block-diagonal decomposition，即块对角分解方法。具体来讲就是：

可以发现，每个线性转换函数都是通过一组低维矩阵$Q_{br}$的和来定义，即：

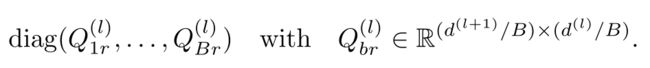
基函数分解可以看作是不同关系类型之间的有效权值共享形式，而块对角分解可以看作是对每种关系类型的权值矩阵的稀疏性约束。块对角分解结构编码了一种直觉，即潜在的特征可以被分为一组变量，这些变量在组内比在组间耦合更紧密。这两种分解都减少了高度多关系数据(如现实的知识库)需要学习的参数数量。

3. 实验

3.1 节点分类

节点分类可以概括如下：

简单来说就是通过堆叠多个R-GCN层以得到节点的向量表示，然后再通过softmax函数得到输出，最后通过计算交叉熵损失函数来更新模型参数，这与前面提到的GNN节点分类模型一致。

交叉熵损失函数定义为：

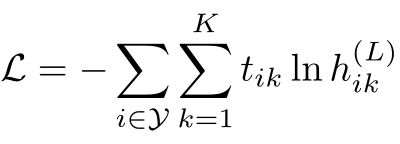
其中$\mathcal{Y}$是有标签的节点的索引集合，$h_{ik}^{(L)}$表示节点$i$的输出中的第$k$项，$t_{ik}$表示对应的标签真实值。

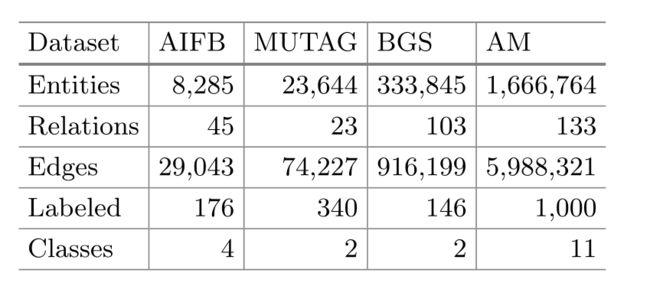
实验所用数据集的实体、关系、边、标签以及类别如下所示：

Baseline：RDF2Vec、Weisfeiler-Lehman kernels (WL) 、Feat（一种手工设计的特征提取器）。

实验结果：

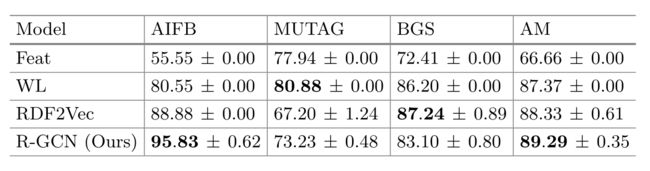
可以发现，R-GCN在MUTAG和BGS上没有表现最好，作者给出的解释为：MUTAG和BGS中高度节点比较多。具体来讲：来自相邻节点的消息聚合的归一化常数$1/c_{i,r}$的固定选择是造成这种行为的部分原因，对于高度节点来说，这可能特别成问题。在未来的工作中，克服这一限制的一种有潜力的方法是引入一种注意力机制，即用数据依赖的注意力权重$a_{ij,r}$替换归一化常数$1/c_{i,r}$。

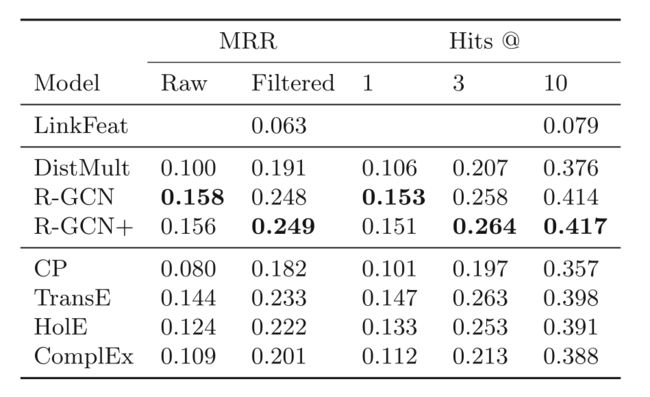
3.2 链接预测

关于链接预测可以参考我之前写的文章：PyG搭建GCN实现链接预测。

链接预测模型分为编码器和解码器，编码器就是R-GCN，即通过R-GCN对节点进行编码以得到低维向量表示，然后通过解码器DistMult也就是评分函数得到节点向量对之间的得分，进而与真实样本求交叉熵损失函数，最后再更新参数。

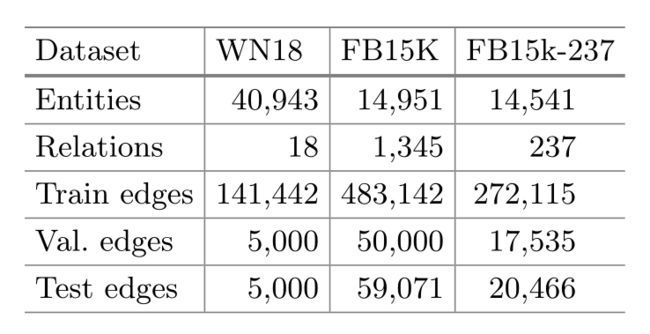
数据集：

实验结果：